Гидроакустическая антенна – это устройство, обеспечивающее пространственно-избирательное излучение или прием звука в водной среде при совместной работе с передающим или приемным устройством. Элементы экранирования часто применяются в гидроакустических антеннах. Сам этот элемент необходим для ослабления электрических или магнитных и электромагнитных полей, при этом элемент экранирования позволяет значительно уменьшить воздействие других электромагнитных полей на конструктивные элементы оборудования. Сами же гидроакустические антенны необходимы при получении или приеме гидроакустических сигналов, при помощи определенных гидроакустических преобразователей. Гидроакустический преобразователь является техническим устройством, у которого основное предназначение это – преобразование электрических колебаний в механические, или, наоборот. Также существует два основных класса гидроакустических преобразователей – это магнитострикционные и пьезоэлектрические. Принцип действия первых основан на эффекте магнитострикции, то есть изменении размеров, а также формы тела при его намагничивании. А принцип действия вторых основан на использовании прямого и обратного пьезоэлектрического эффекта, то есть под действием механических сил, приложенных к кристаллам некоторых веществ, на поверхностях этих кристаллов появляются электрические заряды, величина которых пропорциональна степени деформации. При изготовлении антенн гидроакустических приборов чаще всего используют такой материал, как титан бария.
Рассмотрим класс электроакустических преобразователей. Это устройства, которые преобразуют электрическую энергию в акустическую и обратно. Электроакустические преобразователи, в зависимости от класса преобразования разделяют на приемники и излучатели, например, прием звука в технике связи, для приема и измерения упругих колебаний, гидролокации и тому подобное. Чаще всего электроакустические преобразователи имеют двойное преобразование энергии – электромеханическое. В результате часть, подводимая к преобразователю электрической энергии, переходит в энергию колебаний механической системы. Также существуют электроакустические преобразователи, которые не имеют механической колебательной системы, такого вида излучатели применяются весьма редко. Когда электроакустический преобразователь является излучателем, то на его вход задается электрическое напряжение и ток, определяющее его колебательную скорость и звуковое давление, соответственно в его поле. Подобный теоретический расчет электроакустического преобразователя должен предусматривать установленные связи между его входными и выходными параметрами.
Процессы разработки и расчета элементов экранирования гидроакустических антенн описаны в работах [3–5], а поставленные задачи и их решения, связанные с проблематикой звукоизоляции представлены в работах [1–2, 6–10, 13]. Проведенные исследования по заданной проблематики анализа волновых полей в единичном цилиндрическом полом электроакустическом преобразователе гидроакустической антенны до сих пор являются перспективным направлением в науке. В данной статье рассматривается разработка численно-аналитической методики анализа волновых полей в цилиндрическом полом электроакустическом преобразователе гидроакустической антенны.
Исследование протяженной конструкции экранированного полого электроакустического преобразователя
Исследуем протяженную конструкцию экранированного полого электроакустического преобразователя, который имеет составное поперечное сечение (рисунок). Стоит отметить, что рассматриваемый экранированный полый электроакустический преобразователь отнесен к нормированным цилиндрическим координатам Orθz.
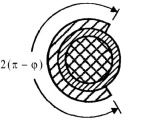
Конструкция экранированного полого электроакустического преобразователя с учетом составного поперечного сечения
Физические и механические свойства, а также линейные, вязкие и упругие свойства материала при деформации, характеризуются функциями плотности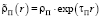 
и соответствующими матрицами:
,
,
.
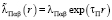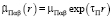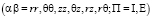Здесь комплексными величинами являются постоянные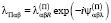 
, 
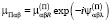, где 
, 
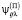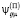являются определенными углами потерь. Задача определения соответствующих характеристик полей исследуется в двумерной модели плоской динамической деформации. Стоит отметить, что исходные соотношения для внешних и внутренних экранирующих элементов включают определенные уравнения динамических упругих деформаций 
:
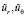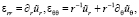
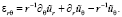
При этом уравнения теории упругости [3], которые связывают напряжение и деформацию упругой среды по обобщенному закону Гука для исследуемого типа в противоположность изотропии функционально-градиентных материалов [11–12, 14], будет следующего вида:
.
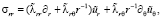
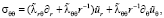
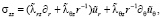
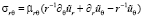Далее рассмотрим уравнения двумерного упругого волнового деформирования [3]:
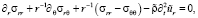
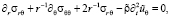
в которых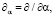 
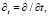t являются параметрами определенного времени. Рассмотрим обобщенные исходные комплексные представления для полей волновых упругих перемещений при учете экранирующих составляющих элементов:
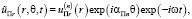
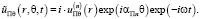
Использование обобщенных исходных комплексных представлений для полей волновых упругих перемещений при учете экранирующих составляющих элементов и при учете уравнения связи динамических упругих деформаций с учетом вектора упругих волновых перемещений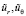 
и преобразованного уравнения обобщенного закона Гука для рассматриваемой задачи, позволит привести к следующему виду:
,
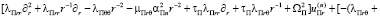
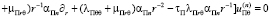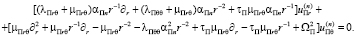
Соотношения рассматриваемой модели включают [14] уравнения электростатики, записываемые с использованием векторов напряженности Eα, индукции Dα, а также потенциала Ф: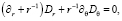 
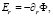
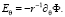Таким образом, определяющие соотношения приобретут следующий вид:
,
,
,
,
.
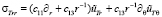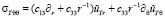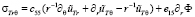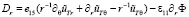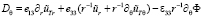Здесь cij является содержащим модули упругости, eij является параметрами, характеризующими свойства пьезоэлектрика как электромеханической колебательной системы, а εij является диэлектрическими проницаемостями.
Методика расчета определенных характеристик волновых полей
Представленная методика основывается на подходе последовательного аналитического интегрирования систем. Формирование представлений для волновых полей осуществляется в следующих областях: SI, ST и SE. Системы амплитудных уравнений волнового деформирования цилиндрически ортотропных материалов, состоящих из твердых зерен карбидов, нитридов и боридов переходных металлов, образующих прочный непрерывный каркас, и металлическую связку, элементов экранирования, может записаться в следующей форме:
,
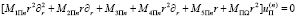где
, 
, 
,
, 
,
, 
.
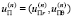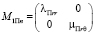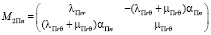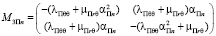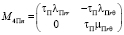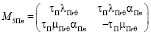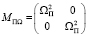Далее проводится интегрирование в степенных рядах следующего вида
.
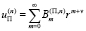Векторные коэффициенты этих рядов из систем рекуррентных соотношений будут
;
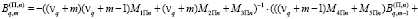
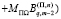
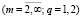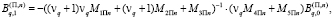
где vq является корнями следующего полиномиального уравнения:
,
,
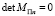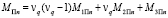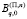является соответствующими значениями vq, которые определены с точностью до произвольного постоянного множителя систем уравнений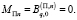 
Будем считать, что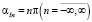 
полагается для области внутреннего экрана SI, следовательно, полученная векторная комплексная характеристика волнового поля, которая является также амплитудной, имеет представление в виде ряда по базисному множеству частных решений с неопределенными коэффициентами:
.
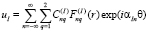Таким образом, сечение внешнего незамкнутого экрана для области SE будет иметь следующую структуру:
.
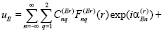
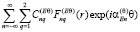Для области ST, в задаваемых в сходной форме получим
,
,
.
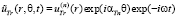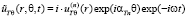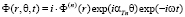При этом используются ряды записываемые в векторной форме относительно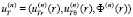 
систем дифференциальных уравнений:
,
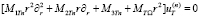где
, 
,
, 
.
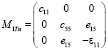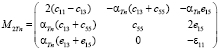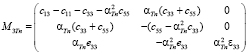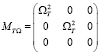Также учитывается, что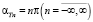 
, следовательно, получаем уравнения следующего вида:
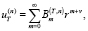
при этом векторные коэффициенты определяются из соответствующих систем рекуррентных соотношений, таких как
,
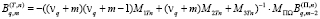
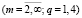где vq является корнями полиномиального уравнения
, 
,
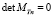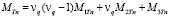а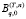 
является соответствующими значениями vq, которые определены с точностью до произвольного постоянного множителя, при этом решения систем однородных алгебраических уравнений будут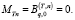 
Таким образом, векторную комплексную амплитудную характеристику электроупругого волнового поля представим в виде ряда по базисному множеству частных решений с неопределенными коэффициентами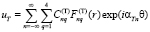 
. Подчинение характеристик волновых полей осуществляется на основе приема квадратичной минимизации:
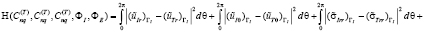
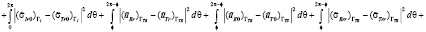
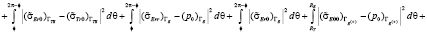
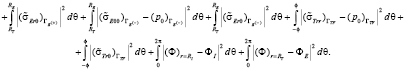
Искомые неизвестные характеристики для конкретных совокупностей определяются соответствующими уравнениями, условия которых
,
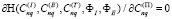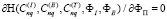[3].
Рекомендуется на участках границ областей SП использовать разложения функций в ряды Якоби – Ангера, для более эффективного вычисления интегралов от характеристик падающей гидроакустической волны.
Заключение
Представленные в работе исследования является весьма актуальными. Результатом исследований является теоретический алгоритм анализа волновых полей в единичных цилиндрических полых электроакустических преобразователях гидроакустических антенн с внутренними цилиндрическими экранами. Проведено исследование протяженной конструкции экранированного полого электроакустического преобразователя, а также исследована методика расчета определенных характеристик волновых полей. Даны рекомендации использования разложения функций в ряды Якоби – Ангера.
Данные исследования уже используются в научно-исследовательских работах Технического института военно-морского флота Вьетнама, а также в опытно-конструкторских работах компаний судостроительного сектора Вьетнама. Перспектива данного исследования заключается в том, что полученные результаты в статье можно применить в исследованиях, например, методов уменьшения гидроакустической активности приборов подводных транспортных средств, а также в моделях функционирования гидроакустических экранов и покрытий для конструкций и приборов подводных транспортных средств.