Метрическая теория программ Холстеда исходит из статического выражения алгоритма на конкретном языке программирования, поскольку лишь программы в машинном коде представляют собой «динамическое» исключение – они могут быть непосредственно выполнены. Все же остальные выражения, или реализации, алгоритмов должны исследоваться в первую очередь по их текстуальным представлениям. Исходя из простых и естественных комбинаторных соображений, а также учитывая структурные особенности исследуемых языков программирования и текстов написанных на них программ, Холстед получает пригодные для практического использования соотношения между основными метрическими характеристиками.
Метрические оценки и характеристики программ по Холстеду такие как, например, длина, время отладки, структурная сложность и другие позволяют оценить априори качество программного обеспечения и среды программирования. Динамическая характеристика сложности – важная оценка не только при выбранном подходе эквивалентности по структуре, но и по функции.
Каждая алгебраическая модель программ строится над выбранным конечным базисом операторных символов и логических переменных, заменивших собой в моделируемых программах операторы и логические условия. При фиксированном базисе все алгебраические модели имеют общее множество своих объектов, и одна отличается от другой отношением эквивалентности объектов. Проблема эквивалентности в отдельной модели состоит в поиске алгоритма, который, получив на свой вход две схемы программ из этой модели, распознаёт, эквивалентны они в ней или нет. Если такой алгоритм найден, то он именуется разрешающим эквивалентность в этой модели.
В теории алгебраических моделей программ установлено существование моделей с неразрешимой проблемой эквивалентности, т.е. таких, для которых нет разрешающих в них эквивалентность алгоритмов. Это обстоятельство и выдвигает задачу разработки методик распознавания эквивалентности в алгебраических моделях программ.
Алгебраическими моделями программ описываются такие модели, как дискретные преобразователи, а именно: для каждого дискретного преобразователя можно построить равносильную ему схему программы. На этом основании факты по разрешению эквивалентности дискретных преобразователей переносятся в теорию алгебраических моделей программ.
Математически, программой x назовем упорядоченную последовательность команд, обеспечивающих отображение x: X>Y, где X – входной вектор, Y – выходной вектор, D(X) – множество входных, D(Y) – множество выходных векторов. Множество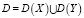 
– множество состояний параметров программы.
Программы x, y эквивалентны функционально [3] (по результату) на X, если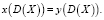 
Пусть d(x) – количество переменных в программе х или введенных в программу переменных (без входных–выходных), f(x) – количество типов операторов и отношений в программе x («if-then-else», «;», «> = », « = », «for-to-do» и т.д.).
Введем операцию сложения программ:
сумма программ x, y с входным вектором D и выходными векторами D1, D2 – это программа z с входным D и результатом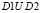 
: 
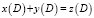. Сложение программ – транзитивно, коммутативно, ассоциативно.
Введем композицию программ:
композиция y*x двух программ x, y, где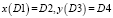 
– программа 
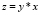такая, что 
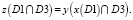D1 принадлежит входному множеству x, D2 и D3 принадлежат подмножеству входного множества y и подмножеству выходного множества x, D1 принадлежит выходному множеству y.
Операций сложения и композиции достаточно для описания структуры любой программы. Как известно, по теореме Бёма – Якопини [5], всякую программу можно представить через три базовые алгоритмические структуры: следование, ветвление, повторение. Опишем их через введенные операции.
Следование X = A>B – это (по определению) композиция X = A*B.
Неполному ветвлению («без иначе») с условием а сопоставим программу A({M, a}) с результатом – множеством M, если а – истинно и пустым множеством, если а – ложно. Формула полного ветвления: X = B*A + C*!A, где !A({M, a}) = A({M, не a}).
Цикл с постусловием, аналогично, имеет формулу вида X = B + A*X. Цикл с предусловием – формулу X = A*(B + X).
Рассмотрим сходимость программ в пространстве программ. Программы x1, x2, x3,…, xn,… сходятся по схеме к программе у, если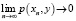 
. Программы сходятся функционально к программе y, если 
.
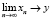Из сходимости по схеме следует функциональная сходимость, обратное неверно.
Пусть M – пространство программ над алфавитами X и Y, M(Pi), i = 1,2,… множество программ которые реализуют одну задачу Pi. Назовем оператором над программой некую функцию A, такую, что A(x) = y.
Операторы An сходятся к оператору A функционально (по схеме), если для любой программы z: An(z) сходятся к A(z) функционально (по схеме).
С точки зрения существования, единственности и построения оптимальной программы, достаточно рассмотреть операторы минимизации:
1) Ad – минимизация по количеству операндов:
, 
),
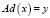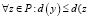где d(y) – количество операндов в y;
2) Af – минимизация по количеству типов операторов:
, 
),
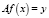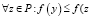где f(y) – количество типов операторов в y;
3) At – минимизация по времени создания программы:
, 
),
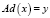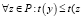где t(y) – время создания программы y, оцениваемая по Холстеду:
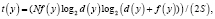
где N – длина программы,
,
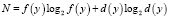S – число Страуда.
«Число Страуда» введено психологом Джоном Страудом в работе «Тонкая структура психологического времени». Дж. Страуд определил «момент» как время, требуемое человеческому мозгу для выполнения наиболее элементарного различения. Он обнаружил, что в течение всего времени бодрствования человек воспринимает эти «моменты» со скоростью «от пяти до двадцати или чуть меньшего числа раз» в секунду. Следует отметить, что, хотя Страуд исследовал лишь скорость мысленной обработки, отличную от скорости ввода-вывода, в диапазон приведенных им цифр попадает число кадров в секунду, превращающее кинофильм из последовательности отдельных снимков в непрерывное изображение. Обозначая через S число страудовских «моментов» в секунду, мы можем записать: 5 < = S < = 20 в секунду.
Естественно, что любой человек, занимающийся реализацией алгоритма, способен в зависимости от степени своей сосредоточенности отвлечь какую-то часть мысленных различений на посторонние предметы. Пользуясь терминологией вычислительной техники, можно сказать, что, если он находится «в режиме разделения времени», S представляет собой лишь верхнюю границу. С другой стороны, если программист выполняет эквивалент машинной операции «запретить все прерывания» и сосредоточивает внимание на программировании, то применимо действительное значение S.
В пространстве X элементов x1, x2, xn,… определим метрику
,
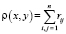где n – количество всех модулей в x, y, rij – сумма весов (длин) дуг орграфа, вершинами которого являются модули x, y, а ребрами – действия над ними.
Ошибка в каждом модуле может оказать воздействие на ошибку в другом модуле, на работу самого модуля (уменьшить или усилить влияние). Меру влияния определим как rij, R = {rij:i = 1,…, n – 1; j = 2,…,n}. Определим в структуру орграфом без петель и кратности ребер: вершины – ошибки (места их локализации), ребра – меры влияния.
Задача – найти такую подстановку, которая минимизирует функционал суммарного влияния для системы со структурой S:
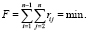
В качестве rij можно взять меру, учитывающую время начала воздействия точек локализации, предшествующих данной xj и интенсивность их влияния. Если можно определить безусловные вероятности наступления событий Si, то такие оценки можно взять байесовыми. Если для событий Si невозможно указать безусловные вероятности их наступления, то применим следующую процедуру.
1. Для каждого события Si указать события {sij}, влияющие на Si. В результате получаем дерево событий. Его нижний уровень – события Sio, для которых можно экспертно указать безусловные вероятности их наступления.
2. Каждый эксперт указывает безусловную вероятность наступления событий Si0, i = 1, 2,…, n0, а также веса pi0 событий. Методом Дельфи (можно средневзвешенным осреднением, учитывая веса pi0) событию данного уровня ставим в соответствие Pi0(t) – вероятность наступления Si0 в момент времени t. Практически функция Pi0(t) задается таблицамиPi0(t1), Pi0(t2) и т.д. Так как на нижнем уровне S0 состоит в одновременном осуществлении независимых событий Si0, i = 1, 2,…, n0, то по теореме умножения вероятностей вычисляем вероятность события S0 в момент времени t:
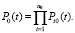
3. Спустя время t после осуществления S0, методом Дельфи, например, дают оценку условной вероятности события S1. Усредняя (с учетом весов), получаем функцию f(t). Далее найдем безусловную вероятность наступления S1 к моменту t:
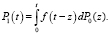
4. Последовательность 1–3 (перехода от верхнего уровня иерархии к нижнему) повторяем для всех уровней, в результате находим функцию P(t) – наступления события S.
Активности модулей взаимодействуют (прямо или косвенно), например, с помощью соотношений [1]:
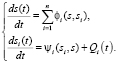
Здесь s(t) – структурная (логическая) активность программ, Qi(t) – функционал меры чувствительности отклонений xi от xiopt. Например, Qi(t) = k||xi – xiopt||, k > 0.
На функции ji(t) = ji(s(t), si(t)), yi(t) = yi(s(t), si(t)) накладываются определенные ограничения, в частности периодичность, затухание, наличие равновесного состояния и др.
Метрика ρ(x, y) определяема и как сумма всех весов ребер орграфов модулей, отличающихся при заданной структуре или отклоняющихся от оптимальной структуры:
.
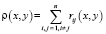Можно метрику задавать и как меру интеллектуальной работы программы, как разность энтропии до начала работы (статическое состояние) и после окончания работы (динамическое состояние).
Макс Планк часто подчеркивал различие между двумя типами изменений, встречающихся в природе. Природа, писал Планк, по-видимому, отдает «предпочтение» определенным состояниям. Необратимое увеличение энтропии описывает приближение системы к состоянию, неодолимо «притягивающему» ее, предпочитаемому ей перед другими, – состоянию, из которого система не выйдет по «доброй воле».
«Согласно этому способу выражения, в природе невозможны те процессы, при которых природа дает меньшее предпочтение конечному состоянию, чем начальному. Предельный случай представляет обратимые процессы; в них природа испытывает одинаковое предпочтение как к начальному, так и к конечному состоянию, и поэтому переход из одного состояния в другое может происходить в обоих направлениях».
Пусть ds/dt – изменение энтропии отлаживаемого программного комплекса, ds1/dt – изменение энтропии за счет структурных изменений, потоков комплекса (открытой системы), ds2/dt – изменение энтропии за счет отладочных усилий. Справедливо уравнение Пригожина [4]: ds/dt = ds1/dt + ds2/dt.
При исследовании программ важно рассматривать пространства векторов x = (x1, x2,… , xn), где xi – характеристика ошибок в программе или структурная связность процедур, ui – количество ошибок в i-ом модуле комплекса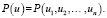 
Можно исследовать операторные «отладочные» уравнения. Пусть u(x, t) – количество ошибок, обнаруженных в программной системе в момент времени t, а х – мера (уровень) ошибок. Рассмотрим уравнение (см. [2]): Lu + Tu = f,
T – оператор, определяющий уровень начальных ошибок в программе, L – некоторый линейный ограниченный оператор отладки, L:U>V, U, V – линейные нормированные пространства D(L)⊆U, R(L)⊆V.
Теорема. Если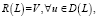 
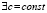: Lu ≥ cu, T < c, то это уравнение имеет единственное решение u∈U.
Доказательство. Условия утверждения гарантируют существование обратного оператора L–1 и его непрерывность, причем L–1 < 1/c. Тогда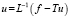 
. Для однородного уравнения
.
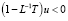Отсюда следует, что u = 0. Неоднородное уравнение имеет единственное решение.
Пример. Пусть umax – максимальный уровень синтаксических ошибок в программе Р, u(t) – оставшееся их количество к моменту времени t. Исходя из модели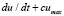 
= 0, u(0) = u0 можно заключить, что уровень ошибок убывает при ca ≠ – 1 (0 < a < T) по закону: u(t) = u0(1 + c(a – t))/(1 + ca).
Если дополнительно задать u(b) = B, то закон изменения ошибок находится по дополнительному значению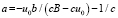 
.
Выводы
Поставлены и исследованы некоторые задачи программирования в метрических пространствах.
Рассмотрены операторные уравнения, оптимизация программ по различным критериям.
Использованы метрические оценки и характеристики программ по Холстеду для оценки априори качества программного обеспечения и среды программирования.
Введены операции сложения программ и композиции программ.
Рассмотрена сходимость программ в пространстве программ.
Рассмотрены операторы минимизации по количеству операндов, по количеству типов операторов, по времени создания программы.
В пространстве элементов определена метрика.
Определена мера влияния.
Рассмотрена задача нахождения такой подстановки, которая минимизирует функционал суммарного влияния для системы со структурой.
Исследованы операторные «отладочные» уравнения.
Доказана теорема о единственности решения неоднородного уравнения для количества ошибок, обнаруженных в программной системе в момент времени при определенных условиях.