Предметные олимпиады – это форма интеллектуальных соревнований школьников в определенной научной области, которая позволяет выявлять не только уровни образовательных достижений учащихся, но и проверяет умение школьников применять полученные знания в новых нестандартных ситуациях при решении заданий повышенной сложности. Предметные олимпиады проводятся c целью выявления и развития у учащихся творческих способностей, интереса к научной (научно-исследовательской) деятельности и для пропаганды научных знаний [1]. Олимпиады являются важнейшим фактором поиска и отбора одаренной молодежи для формирования будущей интеллектуальной элиты страны.
Для учащихся школ предметные олимпиады являются одним из наиболее эффективных способов раскрытия потенциала и степени владения материалом, они способствуют развитию умственных и творческих способностей, активизируют самоконтроль результатов обучения. Участие в таких олимпиадах предполагает развитие способностей у школьников в соответствии с направлением подготовки на углубленном высоком творческом уровне. Рассмотрим на примере олимпиад по информатике основные требования к знаниям и умениям участников и проблемы, с которыми сталкивается педагог при подготовке школьников к этому мероприятию.
Как показывают исследования [5], для успешного участия в олимпиадах по информатике учащийся должен знать:
1) технические характеристики компьютеров;
2) базовые параметры широко распространенных операционных систем;
3) методы формализации поставленных задач;
4) основные типы алгоритмов (алгоритмы работы с различными структурами данных, алгоритмы работы с графами, алгоритмы организации перебора и динамического программирования, алгоритмы целочисленной арифметики, алгоритмы моделирования, алгоритмы компьютерной геометрии и другие);
5) один или несколько языков программирования (список допустимых языков программирования определяют организаторы конкретных олимпиад).
Кроме того предполагается, что потенциальный участник олимпиады должен уметь:
1) работать с персональными компьютерами в современных операционных системах с интегрированными системами программирования;
2) эффективно обходить имеющиеся ограничения по характеристикам компьютеров, например по памяти и быстродействию, при решении задач;
3) переходить от словесного описания постановки задачи к ее формальному описанию с учетом заданных технических и содержательных ограничений;
4) использовать на практике основные типы алгоритмов;
5) применять на практике современные технологии программирования, а также методы отладки и тестирования программ.
Анализ олимпиад по информатике в контексте содержания показал, что они включают задачи модульной арифметики, комбинаторики, задачи по сортировке и перебору данных, динамическому программированию, моделированию, оптимизации, длинной арифметике, линейному и двоичному поиску, жадным алгоритмам, рекурсии, теории графов, комбинаторике и по работе с данными строкового и файлового типов. В качестве примера приведем список алгоритмов олимпиадных задач, которые предлагались участникам регионального этапа Всероссийской олимпиады школьников по информатике в 2016/2017 учебном году [3] (таблица).
Cписок алгоритмов олимпиадных задач
|
Задача |
Алгоритмы, обеспечивающие полное решение задачи |
Алгоритмы, обеспечивающие частичное решение задачи |
|
Задача 1 «Кампус» |
Модульная арифметика, использование формулы |
Линейный поиск |
|
Задача 2 «Калькулятор» |
Динамическое программирование, жадные алгоритмы |
Линейный перебор вариантов |
|
Задача 3 «Размещение данных» |
Алгоритмы на графах (обход в глубину) |
Перебор, линейный поиск |
|
Задача 4 «Полезные ископаемые» |
Двоичный поиск, комбинаторика, алгоритмы на графах (паросочетания в графах) |
Перебор вариантов, жадные алгоритмы, моделирование, алгоритмы поиска максимального паросочетания, алгоритмы поиска максимального потока |
|
Задача 5 «Автоматизированное управление доставкой» |
Линейный перебор вариантов, вывод формулы |
Полный перебор вариантов, динамическое программирование |
|
Задача 6 «Большой линейный коллайдер» |
Линейный проход, структуры данных, комбинаторика |
Полный перебор вариантов, моделирование |
|
Задача 7 «Силовые поля» |
Структуры данных, сканирующая прямая |
Перебор, сортировка |
|
Задача 8 «Повышение квалификации» |
Работа с деревьями, алгоритмы на графах (обход в глубину), сортировка событий |
Линейный перебор вариантов |
В настоящее время в качестве основных документов при определении содержания задач для проведения школьных олимпиад по информатике используются федеральные государственные образовательные стандарты среднего общего образования по информатике и ИКТ базового и профильного уровней [2]. Как показывает многолетняя практика, основной проблемой при подготовке школьников к олимпиадам является то, что раздел «Алгоритмизация и программирование» базового или профильного курсов «Информатика и ИКТ» обеспечивает только обязательный общеобразовательный минимум знаний по данным темам, но для полноценной подготовки школьников к олимпиадам этого минимума недостаточно. Анализ задач олимпиад по информатике представляет собой вполне самостоятельный учебный раздел, который по теоретическим и практическим вопросам выходит за рамки школьный программы и требует особого уровня подготовки и дополнительного времени.
Это привело к тому, что педагоги, заинтересованные в полноценной подготовке участников олимпиад по информатике, организуют дополнительные внеклассные занятия, которые проводятся в виде спецпрактикумов, элективных курсов, тематических и предметных кружков.
Общая подготовка учащихся к олимпиадам по информатике традиционно проходит по нескольким направлениям [5]:
1) отбор одаренных учащихся;
2) тестирование учащихся с целью определения уровня их подготовленности по предмету;
3) развитие навыков работы с компьютером;
4) овладение одним из базовых языков программирования;
5) изучение алгоритмов, необходимых для решения олимпиадных задач;
6) ознакомление с различными способами решения и распознавания применимости известных алгоритмов;
7) анализ программного кода реализации типовых алгоритмов;
8) анализ эффективности программ;
9) изучение методов тестирования программ;
10) формирование приемов написания и отладки программ на компьютере;
11) тренинг: программирование, отладка и тестирование задач;
12) психологическая подготовка участников олимпиад.
Для решения проблемы качественной подготовки участников олимпиады была разработана и внедрена на практике в рамках учреждения дополнительного образования на базе факультета довузовской подготовки Волгоградского государственного технического университете методика подготовки школьников к олимпиадам по информатике [4].
Предметная часть методики была определена после анализа содержания задач олимпиад по информатике. Основными темами для изучения стали линейный и двоичный поиск, сортировка и перебор данных, динамическое программирование, моделирование, оптимизация, длинная арифметика, «жадные» алгоритмы, рекурсия, теория графов, комбинаторика и работа с данными строкового и файлового типов.
При подготовке школьников к олимпиадам по каждому разделу олимпиадной информатики рассматривалось несколько видов задач. Набор из нескольких задач объединялся в систему задач [6]. Понятие «система задач» рассматривалось как совокупность задач, определенным образом связанных между собой и имеющих несколько уровней организации, находящихся в отношении последовательного подчинения. Было учтено, что в системы задач обычно включают типовые задачи, позволяющие школьникам получить навыки работы с типовыми алгоритмами, и неопределенные задачи, которые помогают ученикам развивать творческое мышление [5].
Для примера рассмотрим несколько задач из системы задач на изучение метода двоичного (бинарного) поиска.
У (условие) – задан упорядоченный массив.
Б (базис) – базовые навыки работы с одномерными массивами: просмотр всего массива или его части и вычисление индекса элемента по заданному условию.
Т (требование) – в простейшем случае в упорядоченном массиве требуется найти элемент с заданным значением.
С (способ) – для эффективного нахождения в отсортированном массиве элемента со значением x воспользуемся алгоритмом двоичного (бинарного) поиска, в котором на каждом шаге область поиска уменьшается вдвое. Для этого в заданном массиве (для примера массив упорядочен по возрастанию) выберем средний элемент.
По отношению к значению x средний элемент массива может быть: 1) равен x, в этом случае поиск завершается; 2) больше x – поиск необходимо продолжать в левой части массива; 3) меньше x – поиск необходимо продолжить в правой части массива.
В случаях 2–3 поиск продолжается. Для этого в выделенной части массива вновь выбирается средний элемент и проводятся аналогичные рассуждения. Процесс продолжается до тех пор, пока поиск не будет завершен. Это произойдет в одном из двух случаев: 1) элемент найден, т.е. средний элемент рассматриваемого участка будет равен x; 2) элемент не найден, т.е. длина области поиска уменьшилась до нуля и левая и правая границы области поиска сомкнулись.
Типовая задача 1 (Т1). Опишите массив записей, содержащих фамилию абонента и номер его телефона. Запрограммируйте двоичный поиск в телефонном справочнике.
Задача получена добавлением в условие базовой задачи: исходные данные представлены в виде одномерного массива, каждый элемент которого состоит из двух полей записи.
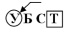
Типовая задача 2 (Т2). Индексом называется таблица, содержащая отсортированные значения некоторых ключей и их местоположение в массиве записей. Индексом пользуются для ускорения поиска в массиве (сам массив может быть неотсортированным). Запрограммируйте процедуру составления индекса и бинарного поиска при помощи индекса.
Задача получена из предыдущей типовой задачи добавлением в требование и добавлением в условие – элементам массива требуется присвоить индексы и выполнить бинарный поиск по индексам, а не по элементам, в отличие от стандартной типовой задачи.
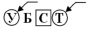
Неопределенная задача 3 (Н3). Пусть некоторый текст T задан в виде последовательности символов, состоящий из слов, и есть два списка из нескольких слов в виде двух массивов A и B. Написать программу, преобразующую текст T в текст S путем замены каждого вхождения слова A[i] на соответствующее слово B[i].
Задача получена из базовой задачи добавлением в условие дополнительных массивов и добавлением в требование – требуется преобразовать исходный текст с использованием алгоритма поиска.
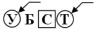
Неопределенная задача 4 (Н4). Дан массив из строк (например, фамилий). Отсортировать его по алфавиту и написать процедуру вставки новой фамилии после заданной так, чтобы алфавитный порядок не нарушился. Предусмотреть ситуацию, когда массив заполнен «до отказа» и вставка нового элемента невозможна.
Задача получена из типовой задачи 2 путем добавления в требование: необходимо вставить новый элемент в массив.
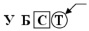
Использование методики предполагает, что предметная часть обучения может быть организована в очной и дистанционной форме. Занятия с учащимися проходили в рамках малой группы. При проведении занятий учитывалось, что в группе есть учащиеся с разными уровнями подготовки (высоким, средним и низким). В качестве основных форм организации обучения были выбраны лекционно-практические и лабораторные занятия.
Обучение по каждой теме проходило в три этапа.
Этап 1 (лекционный). Типовое лекционное занятие в рамках дидактической единицы начиналось с изучения теоретических основ предметной области посредством рассмотрения базовых алгоритмов решения задач данного типа. Для всех рассматриваемых тем были подготовлены системы задач. При очном обучении алгоритм решения типовых задач изучался под руководством преподавателя, при дистанционном обучении учащиеся самостоятельно осваивали материалы, используя кейсы.
Этап 2 (практический). Для проверки усвоения рассмотренного материала в системы задач были внесены дополнительные типовые задачи, которые учащиеся в зависимости от уровня подготовки разбирали с помощью преподавателя, совместно с другими учащимися в рамках работы малой группы или самостоятельно. При разборе задач преподаватель с учащимися анализировал условия задач, определяя их достаточность или избыточность. После решения нескольких типовых задач из системы и консультаций с преподавателем считалось, что школьники получили базовые знания по данной теме и могут приступать к самостоятельному решению задач.
Этап 3 (лабораторный практикум). Во время лабораторного практикума учащимся предлагалось несколько задач с неопределенными условиями (т.е. нестандартных задач) для самостоятельного решения. Для того, чтобы каждый учащийся в процессе обучения смог бы решать задачи на максимальном для себя «пороге трудности», для лабораторного практикума преподаватель выбирал задачи трех категорий (наличие задач из каждой категории обязательно): 1) задачи, которые самостоятельно могут решить все учащиеся, 2) задачи, которые могут решить самостоятельно учащиеся, имеющие уровень подготовки не ниже средней, 3) задачи, которые могут решить самостоятельно только несколько учащихся с высоким уровнем подготовки.
Разработанная методика [5] решает проблемы при подготовке к олимпиадам по информатике, опираясь на выполнение следующих дидактических условий:
1) наличие разработанных специализированных систем задач, охватывающих основные разделы олимпиадной информатики и построенных на основе задач из общероссийской базы заданий олимпиад по информатике;
2) использование систем задач, которые позволяют корректировать процесс обучения в зависимости от достигнутого уровня подготовки и индивидуальных особенностей учащихся;
3) конструирование и реализация индивидуальных образовательных траекторий в рамках учебных занятий (очных и/или дистанционных) по подготовке к олимпиадам по информатике;
4) постоянный мониторинг предметных знаний, умений в области программирования;
5) предоставление возможностей для проявления каждым школьником его способностей на максимально возможном уровне за счет работы в динамичных малых группах и, при необходимости, самостоятельной работы с дистанционной поддержкой со стороны преподавателя;
6) наличие у педагога опыта подготовки школьников к олимпиадам;
7) наличие программной и материально-технической базы для очного и дистанционного обучения школьников.
Таким образом, предложенная методика подготовки школьников к олимпиадам по информатике позволяет не только активизировать познавательные и творческие способности учащихся, но и способствует эффективному решению проблемы качественной подготовки участников олимпиады.



