С целью расширения возможностей компьютерного моделирования различных систем и процессов проведена серия компьютерных экспериментов, выполненных на основе программ расчета групп симметрии. Выберем вначале для описания классической симметрии простых геометрических фигур хорошо известный в теории групп симметрии [5] способ представления, основанный на построении таблиц Кэли. Каждая операция в таблице Кэли кодируется двухстрочной матрицей перестановок или подстановок (permutation and substitution) вида
g[1] = 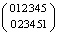 ,
,
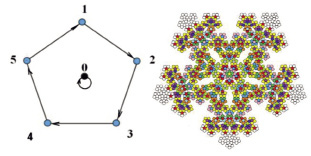
где g[1] – символ 1-й операции. В данном случае эту конкретную запись можно отнести к операции поворота правильного пятиугольника (или к циклической перестановке его вершин) по направлению, определенному ориентированным циклическим графом (рис 1, а). В работе [3] показан способ перехода к более сложной структуре с использованием операции свертки (копирования). Этот прием основан на замене каждой точки структуры точками нового фрагмента, что порождает в данном случае мозаику с симметрией 5-го порядка (рис 1, б). Результаты компьютерного расчета таблицы умножения подстановок (таблицы Кэли) для подгруппы поворотов правильного пятиугольника (рис. 1, а) представлены в табл. 1.
а) б)
Рис. 1. Пятиугольник с центральной точкой (а) и мозаика, выполненная на его основе (б) методом копирования (свертки)
Векторами на рис. 1, а выделена структура орграфа операции подстановок g[1] из табл. 1.
Таблица 1
Таблица Кэли подгруппы поворотов пятиугольника и структура операций
|
g[0] = (0 1 2 3 4 5); (0)(1)(2)(3)(4)(5); |
g[0] |
g[1] |
g[2] |
g[3] |
g[4] |
|
g[1] = (0 2 3 4 5 1); (0) (1 2 3 4 5); |
g[1] |
g[2] |
g[3] |
g[4] |
g[0] |
|
g[2] = (0 3 4 5 1 2); (0) (1 3 5 2 4); |
g[2] |
g[3] |
g[4] |
g[0] |
g[1] |
|
g[3] = (0 4 5 1 2 3); (0) (1 4 2 5 3); |
g[3] |
g[4] |
g[0] |
g[1] |
g[2] |
|
g[4] = (0 5 1 2 3 4); (0) (1 5 4 3 2); |
g[4] |
g[0] |
g[1] |
g[2] |
g[3] |
В теории групп показано, что всякая конечная группа симметрии изоморфна соответствующей группе подстановок (теорема Кэли), поэтому для операции, выбранной выше, возможно ввести «матричное представление», описывающее вращение в двумерном пространстве на угол 72 ° вокруг центральной точки. Выбор в пользу представления с помощью подстановок в данной работе сделан на основании двух соображений. Во-первых, из-за простоты записи операции, кодировку которой можно еще упростить, записывая только нижние строки. В приведенном примере это будет выглядеть следующим образом: g[1] = (023451). Во-вторых, вследствие независимости кодировки операций подстановок от размерности пространства, что особенно важно, когда речь идет о пространствах состояний, топология и размерность которых могут быть и неизвестными.
Модель группы подстановок с нарушенной симметрией
Дальнейший переход к нарушенной симметрии обусловлен большим количеством проблем, возникающих в различных областях науки в тех случаях, когда появляется необходимость описания явлений роста и эволюционных процессов, но, как известно, только «диссимметрия творит явление» (принцип П. Кюри). Под термином «диссимметрия» будем понимать не только «недостаточную» симметрию, но и «псевдосимметрию» [6], а также «нарушенную симметрию».
Авторам данной работы не удалось обнаружить ни одного примера научных исследований процессов накопления, роста и эволюции, в которых принцип Кюри не выполняется в той или иной форме. Поэтому в философии естествознания и социально-экономических процессах он играет существенную роль. Нашей задачей явился поиск математической модели нарушенной симметрии, для чего были использованы разработанные ранее компьютерные методики построения и «визуализации» групп симметрии [8].
В частности, ниже представлены начальные результаты новых исследований, которые привели к обнаружению во множестве бинарных операций полугрупп подстановок с интересными свойствами, названных нами группами нарушенной симметрии (ГНС). «Работу» принципа нарушенной симметрии продемонстрируем на двух примерах, относящихся к различным направлениям исследований: естественнонаучному и социально-экономическому.
Пример 1. Все известные физические эффекты в кристаллах описываются на основе принципа Неймана – Кюри: симметрия структуры и симметрия «воздействия» на структуру складываются таким образом, что в результате остаются только те элементы (преобразования), которые являются общими. Рост кристаллов, в частности, начинается с одной точки (дефекта), в которой нарушена симметрия однородности расплава (рис. 2).

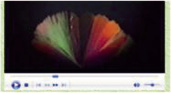
Рис. 2. Два этапа реального процесса роста кристаллов гипосульфита из расплава
Пример 2. Рассмотрим процесс роста цен, который возник в результате нарушения симметрии однородного «хаоса» на бирже, торгующей золотом [3]. Процесс изменения цен (с 2000 г.) можно описать с помощью использования в качестве «биржевого робота» модели мозаики [2] с симметрией 5-го порядка (по рис. 1, б). Числа Фибоначчи, которые часто возникают в экономических моделях, были обнаружены в мозаике при подсчете количества пятиугольников, распределенных на рис. 1, б послойно. Таким образом, получается числовой набор, представленный на диаграмме (рис. 3, а). Поиск аналогичной реальной финансово-экономической системы привел к хорошему совпадению максимумов чисел на диаграмме со сводками на Лондонской бирже, торгующей золотом (рис. 3, б). Наблюдается совпадение положений максимумов в модели (рис. 3, а) с максимумами реальной диаграммы цен на золото (рис. 3, б) и соответствие числам типа Фибоначчи. Этот факт, в частности, позволяет прогнозировать положение во времени следующего взлета цены до середины 2017 г. с резким последующим падением и возможным очередным резким подъемом только через 8 лет. Прогноз строится по точкам фигуры с симметрией оси 5-го порядка (рис. 1, б) и диаграмме (рис. 3, а).

а) б)
Рис. 3. Диаграммы модельного (а) и реального изменения цены на золото (б)
Важно определить, каким образом возникло это нарушение однородной и изотропной симметрии биржевого «хаоса» с образованием симметрии 5-го порядка, отраженной в числах (рис. 3). Возможны два варианта: либо естественным путем, либо направленным действием интеллекта. В первом случае – «Природа Рынка играет» с нами, а во втором – мы играем друг с другом. Исследование нарушенной симметрии, таким образом, становится все более актуальным не только для современной физики, которая представляет собой локально перенормируемую квантовую теорию неабелевых калибровочных полей со спонтанно нарушенной симметрией, но и для других реальных систем, в каждой из которых появляется свой «бозон Хиггса». В микробиологии и генной инженерии хорошо известна роль «дефектов» в кодировке ДНК [7]. В радиоэлектронике нарушение симметрии антенны токами проводимости приводит к ее диаграмме направленности [4]. Технически, решаемая в данной статье задача ближе всего подходит к проблемам «ошибок кода» при передаче информации в компьютерных сетях и программах расчетов с большими числами.
Введем простой дефект, то есть «случайную ошибку кода» в записи элемента g[1] в программу расчета группы подстановок и таблицы умножения: вместо g[1] = (023451) (из табл. 1) запишем курсивом новую подстановку следующим образом: g[1] = (023431). Если затем произвести такие же операции умножения, которые были применены ранее при построении таблицы Кэли, то получим новую конечную таблицу подмножества произведений бинарных операций (табл. 2).
Таблица 2
Таблица 5х5 подмножества произведений бинарных операций на множестве из 6 чисел
|
g[0] = (0 1 2 3 4 5); |
g[0] |
g[1] |
g[2] |
g[3] |
g[4] |
|
g[1] = (0 2 3 4 3 1); |
g[1] |
g[2] |
g[3] |
g[4] |
g[3] |
|
g[2] = (0 3 4 3 4 2); |
g[2] |
g[3] |
g[4] |
g[3] |
g[4] |
|
g[3] = (0 4 3 4 3 3); |
g[3] |
g[4] |
g[3] |
g[4] |
g[3] |
|
g[4] = (0 3 4 3 4 4); |
g[4] |
g[3] |
g[4] |
g[3] |
g[4] |
Очевидно, что эта таблица не является таблицей Кэли, так как в ней отсутствуют, в частности, обратные элементы, поэтому можно говорить, что «ошибка» в записи (в кодировке) элемента группы симметрии привела к нарушению симметрии. Исходя из принципа Кюри, предполагаем, что следует ожидать появление новых свойств в структурах, представленных таким множеством преобразований. Расширим новую группу очередной «неклассической операцией» подстановки g[5] = (012343), не изменяя правила произведения. В компьютерном эксперименте, выполненном по программе расчета таблицы умножения элементов группы, получим расширенное конечное множество операций (табл. 3).
Таблица 3
Таблица 9х9 подмножества произведений бинарных операций на множестве из 6 чисел
|
g[0] = (0 1 2 3 4 5); |
g[0] |
g[1] |
g[2] |
g[3] |
g[4] |
g[5] |
g[6] |
g[7] |
g[8] |
|
g[1] = (0 2 3 4 3 1); |
g[1] |
g[2] |
g[3] |
g[4] |
g[3] |
g[1] |
g[2] |
g[3] |
g[4] |
|
g[2] = (0 3 4 3 4 2); |
g[2] |
g[3] |
g[4] |
g[3] |
g[4] |
g[2] |
g[3] |
g[4] |
g[3] |
|
g[3] = (0 4 3 4 3 3); |
g[3] |
g[4] |
g[3] |
g[4] |
g[3] |
g[3] |
g[4] |
g[3] |
g[4] |
|
g[4] = (0 3 4 3 4 4); |
g[4] |
g[3] |
g[4] |
g[3] |
g[4] |
g[4] |
g[3] |
g[4] |
g[3] |
|
g[5] = (0 1 2 3 4 3); |
g[5] |
g[6] |
g[7] |
g[8] |
g[7] |
g[5] |
g[6] |
g[7] |
g[8] |
|
g[6] = (0 2 3 4 3 4); |
g[6] |
g[7] |
g[8] |
g[7] |
g[8] |
g[6] |
g[7] |
g[8] |
g[7] |
|
g[7] = (0 3 4 3 4 3); |
g[7] |
g[8] |
g[7] |
g[8] |
g[7] |
g[7] |
g[8] |
g[7] |
g[8] |
|
g[8] = (0 4 3 4 3 4); |
g[8] |
g[7] |
g[8] |
g[7] |
g[8] |
g[8] |
g[7] |
g[8] |
g[7] |
Легко, в частности, проверить, что g[1]×g[2] = (023431)×(034342) = (043433) = g[3].
Будем по-прежнему считать, как это было показано в работе [8], что каждому преобразованию из элементов множества бинарных преобразований симметрии можно поставить в соответствие (визуализировать) некоторую структуру, описание преобразований в которой следует вести в терминах «подстановки», анализируя структуру самой подстановки. Новые неклассические «подстановки» (substitution, но не permutation) группы с нарушенной симметрией, записанные теперь в табл. 3 (если сравнивать с табл. 1), получат двумерную (в виде «цветного ожерелья») или одномерную геометрическую интерпретацию (в виде диаграмм). Демонстрационный результат визуализации подстановок представлен на рис. 4 для трех произвольно выбранных операций из этой таблицы.
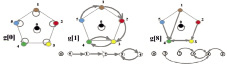
Рис. 4. Структуры подстановок (по табл. 3): g[0] = (012345) = (0)(1)(2)(3)(4)(5); g[1] = (0 2 3 4 3 1) = (0)[5 1 2 (3 4)]; g[8] = (0 4 3 4 3 4 ) = (0)[1(4 3)][2 (3 4)][5 (4 3)]
В одном из проведенных нами компьютерных экспериментов с неклассическими подстановками числовое множество из 34 значений чисел составило множество преобразований, содержащее 91 элемент в таблице произведений. Оказалось, что в этой полной таблице умножения удается выделить 4 операции (включая g[0]), которые образуют небольшое замкнутое подмножество преобразований, приведенное в табл. 4. Это подмножество является циклическим с образующим элементом g[1].
Таблица 4
Таблица умножения конечного подмножества из 4-х преобразований
|
g[0] = (0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33); |
g[0] |
g[1] |
g[2] |
g[3] |
|
g[1] = (10 14 18 21 25 27 29 21 25 4 31 4 31 6 16 6 16 8 16 8 10 18 10 18 12 16 12 14 14 16 23 16 23 28); |
g[1] |
g[2] |
g[3] |
g[3] |
|
g[2] = (31 16 16 18 16 14 16 18 16 25 16 25 16 29 16 29 16 25 16 25 31 16 31 16 31 16 31 16 16 16 18 16 18 14); |
g[2] |
g[3] |
g[3] |
g[3] |
|
g[3] = (16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16); |
g[3] |
g[3] |
g[3] |
g[3] |
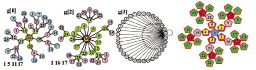
а) б)
Рис. 5. Структуры преобразований с конвергентными свойствами: (а) структуры из 34 точек (g[1] – g[3], табл. 4) и (б) структура мозаики из 36 точек (g[1], табл. 6)
Визуализация структур операций этого подмножества (кроме тождественного преобразования g[0]) представлена на рис. 5, а.
Очевидно, что структура операции g[3] (рис. 5, а) представляет собой орграф с конвергентными свойствами (все пути, сходящиеся к точке). Правая часть табл. 4, то есть таблица произведений g[0] – g[3], может рассматриваться как основание для формулировки теоремы «О существовании множества преобразований с конвергентными свойствами структуры орграфа». Легко показать, что для любой таблицы (с любым конечным количеством элементов), структурно построенной по аналогии с табл. 4, обязательно существует одно преобразование, которое можно записать единственным значением числа R. В структуре орграфа эту точку, к которой сходятся все пути (так же, как на рис. 5, а для g[3], R = 16), назовем условно «Рим» (по старинной поговорке: «все дороги ведут в Рим»), а множество элементов такой таблицы, в которой существует «римская» точка, «римским множеством преобразований».
Результаты исследования и их обсуждение
Ниже представим перечень результатов исследований, полученных в компьютерном эксперименте, которые могут быть применены для дальнейшего анализа и изучения структур с группами нарушенной симметрии (ГНС).
1. Операция g[7] в римском множестве табл. 5 выполняет роль «нуля», так как ее применение к другим операциям множества элементов оставляет g[7] в качестве результата: «нуль на что не умножай, остается нулем». Таким образом, римское множество бинарных операций имеет «единицу» (g[0]) и «ноль» (g[7]), но не имеет обратных элементов.
Таблица 5
Таблица умножения преобразований с «римской точкой» на множестве из 8 точек
|
g[0] = (0 1 2 3 4 5 6 7); |
g[0] |
g[1] |
g[2] |
g[3] |
g[4] |
g[5] |
g[6] |
g[7] |
|
|
g[1] = (1 2 3 4 5 6 7 7); |
g[1] |
g[2] |
g[3] |
g[4] |
g[5] |
g[6] |
g[7] |
g[7] |
|
|
g[2] = (2 3 4 5 6 7 7 7); |
g[2] |
g[3] |
g[4] |
g[5] |
g[6] |
g[7] |
g[7] |
g[7] |
|
|
g[3] = (3 4 5 6 7 7 7 7); |
g[3] |
g[4] |
g[5] |
g[6] |
g[7] |
g[7] |
g[7] |
g[7] |
|
|
g[4] = (4 5 6 7 7 7 7 7); |
g[4] |
g[5] |
g[6] |
g[7] |
g[7] |
g[7] |
g[7] |
g[7] |
|
|
g[5] = (5 6 7 7 7 7 7 7); |
g[5] |
g[6] |
g[7] |
g[7] |
g[7] |
g[7] |
g[7] |
g[7] |
|
|
g[6] = (6 7 7 7 7 7 7 7); |
g[6] |
g[7] |
g[7] |
g[7] |
g[7] |
g[7] |
g[7] |
g[7] |
|
|
g[7] = (7 7 7 7 7 7 7 7); |
g[7] |
g[7] |
g[7] |
g[7] |
g[7] |
g[7] |
g[7] |
g[7] |
РИМ |
2. Переход к орграфу с расходящимися векторами («все дороги выходят из Рима») формально можно представить «обратными» операциями g [1] -1, в матрицах подстановок которых верхняя и нижняя строка меняются местами. Очевидно, что конвергентные и дивергентные свойства обратны друг другу. В частности, g[1]-1 будет представлена следующим образом: 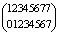 . Произведение g[1] х g[1] -1 = g[0] и т.д. Поэтому описание множеств с дивергентными свойствами расходимости орграфа структуры определяется простым переходом в записи: от обычных матриц подстановок к обратным.
. Произведение g[1] х g[1] -1 = g[0] и т.д. Поэтому описание множеств с дивергентными свойствами расходимости орграфа структуры определяется простым переходом в записи: от обычных матриц подстановок к обратным.
3. Возвращаясь к структурам с симметрией оси 5-го порядка, приведем пример описания мозаики с конвергентными свойствами орграфа структуры. Построение мозаики (рис. 5, б) выполнено копированием пятиугольников по точкам структуры правильного пятиугольника на первом этапе «свертки». Образовавшийся фрагмент копируется еще раз, и эту процедуру можно выполнять многократно, имитируя эволюционный процесс «раздувания» структуры (по аналогии с рис. 1, б). После второго этапа (36 точек на рис. 5, б) математическая модель группы нарушенной симметрии будет записана так, как это представлено в табл. 6.
Таблица 6
Таблица умножения преобразований с «римской точкой» (по рис. 5, б)
|
g[0] = (0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35); |
g[0] |
g[1] |
g[2] |
g[3] |
g[4] |
|
g[1] = (0 0 0 0 0 0 9 6 6 1 6 6 16 12 12 12 2 12 23 18 18 18 18 3 25 4 24 24 24 24 32 30 5 30 30 30); |
g[1] |
g[2] |
g[3] |
g[4] |
g[4] |
|
g[2] = (0 0 0 0 0 0 1 9 9 0 9 9 2 16 16 16 0 16 3 23 23 23 23 0 4 0 25 25 25 25 5 32 0 32 32 32); |
g[2] |
g[3] |
g[4] |
g[4] |
g[4] |
|
g[3] = (0 0 0 0 0 0 0 1 1 0 1 1 0 2 2 2 0 2 0 3 3 3 3 0 0 0 4 4 4 4 0 5 0 5 5 5); |
g[3] |
g[4] |
g[4] |
g[4] |
g[4] |
|
g[4] = (0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0); |
g[4] |
g[4] |
g[4] |
g[4] |
g[4] |
Операция g[1] является «образующим элементом» группы. Орграф структуры этой операции легко сопоставить с мозаикой (рис. 5, б).
4. Еще один вывод следует из факта существования римского множества: свойство дивергенции орграфа ведет к ситуации, когда все точки структуры становятся различимыми и переходят только сами в себя. Это конечная операция «единицы» g[0]-1. Конвергенция же, наоборот, приводит к абсолютной симметрии, когда все точки структуры становятся неразличимыми. Это конечная операция «нуля» g[R].
Заключение
В компьютерном эксперименте, при изучении структур преобразований с нарушенной симметрией, обнаружены новые («римские») множества: с «нулем», «единицей», без обратных элементов, с конвергентными (сходимостью) и дивергентными (расходимостью) свойствами орграфа структуры. Существует возможность перехода от множества преобразований с конвергентными свойствами орграфа структуры к структурам множеств с дивергентными свойствами, заменой неклассических матриц с нарушенной симметрией на обратные матрицы подстановок. Этот подход наглядно демонстрирует рождение эволюционных деревьев орграфа структуры и в то же время выделяет самый общий аспект исследований, важный для экономики, микробиологии, кристаллографии, астрофизики. Проблема, очевидно, выходит за рамки одной статьи, однако еще раз показывает, каким образом обнаруженное в кристаллографии П. Кюри нарушение симметрии «творит явление». Всякое явление, обнаруженное в природных и социально-экономических системах, подчиняется принципу нарушения симметрии, который определяет динамику изменения симметрии и свойств системы. С точки зрения теории множеств всякое множество бинарных преобразований всегда подчиняется требованию ассоциативности и, в общем случае, является полугруппой.
Работа поддержана грантом РФФИ № 14-02-97504.



