В сравнении с движением жидкости вдоль гидравлически гладкой поверхности движение жидкости вдоль шероховатых поверхностей в расчетно-теоретическом плане изучено в значительно меньшей мере. Тем не менее, даже при расчете течения вдоль гидравлически гладкой поверхности, вблизи стенки предпочитают использовать простейшие аппроксимационные зависимости [4]. Классические работы по движению жидкости в трубопроводах с песочной шероховатостью стенки, выполненные И. Никурадзе, на первый взгляд, имеют чисто теоретический интерес. Однако, например, при движении водопесчаных потоков при небольших скоростях вдоль нижней образующей трубы возможно образование неподвижного слоя песчаных частиц, в результате чего в этой области течения создаются условия, которые близки к условиям в опытах И. Никурадзе. Поэтому дальнейшее совершенствование методов расчета течения вдоль поверхности с песочной шероховатостью имеет не только теоретический аспект, но и практическое значение в задачах гидротранспортирования измельченных твердых материалов по трубопроводам.
Традиционно, при движении жидкости вдоль поверхности с песочной шероховатостью различают три характерных области.
1. Режим течения без проявления шероховатости
где λ – коэффициент гидравлического сопротивления; ks – величина песочной шероховатости стенки; υτ – динамическая скорость; ν – кинематическая вязкость жидкости; Re – число Рейнольдса, рассчитанное по диаметру трубы, средней скорости и кинематической вязкости жидкости.
По данным различных авторов, эмпирическая величина α несколько различается, так по [3] α = 3 и по [5] α = 5.
2. Режим течения с полным проявлением шероховатости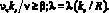 
По данным различных авторов эмпирическая величина также β несколько различается, так по [3] β = 60 и по [5] β = 70.
3. Переходной режим течения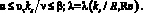 
Отличительной чертой переходного режима течения является наличие минимума значения коэффициента гидравлического сопротивления, положение которого определяется величинами ks/R и Re (см. рис. 1).
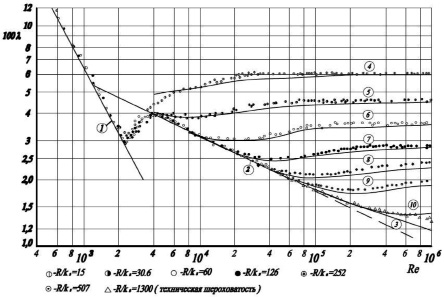
Рис. 1. Закон сопротивления для гладких и шероховатых труб. Кривая 1 соответствует ламинарному режиму течения. Кривая 2 соответствует формуле Блазиуса. Кривая 3 соответствует формуле Прандтля. Кривые 4–10 расчет по формулам (5)–(9)
Для расчета профилей скорости и коэффициентов гидравлического сопротивления при режимах течения без проявления шероховатости и с полным проявлением шероховатости имеются вполне приемлемые с точки зрения погрешности расчетные соотношения (см., например, [3, 5]).
Применительно к переходному режиму течения можно отметить следующее. В работах [3, 5] показано, что на основе теоретического анализа экспериментальных данных И. Никурадзе расчет профиля скорости и коэффициента гидравлического сопротивления может быть выполнен с помощью зависимости
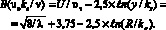(1)
Экспериментальная зависимость величин B(υτks/ν) от безразмерной величины ?g(υτks/ν) показана на рис. 2. Из выражения (1) следует, что если известен аналитический вид зависимости B(υτks/ν), то по формуле (1) можно определить профиль скорости для y ≥ ks и коэффициент гидравлического сопротивления λ. Верно и обратное, если независимым способом определяется, например, величина λ, то по формуле (1) можно определить величину B(υτks/ν) и профиль скорости.
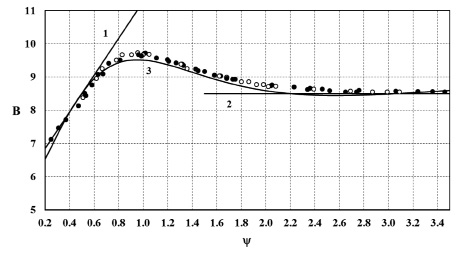
Рис. 2. Зависимость величины В от ψ. Кривая 1 соответствует режиму без проявления шероховатости. Кривая 2 соответствует режиму с полным проявлением шероховатости. Кривая 3 – расчет по формуле (2)
В статьях [1, 2] авторов настоящей работы, рассмотрены опубликованные в технической литературе работы, в которых использовались различные варианты получения аналитических зависимостей, для расчета коэффициента гидравлического сопротивления и профиля скорости при переходном режиме течения. Проведенный анализ показал, что полученные расчетные соотношения не могут использоваться при переходном режиме, поскольку они не обеспечивают совпадения с опытными данными в области минимальных значений коэффициентов гидравлического сопротивления. Предложенные расчетные зависимости лишь обеспечивают плавный переход от режима течения вдоль гидравлически гладкой поверхности к режиму течения с предельным проявлением шероховатости.
В работе [1], в соответствии с подходом, связанным с обсуждением выражения (1), при переходном режиме функция B = В(υτks/ν) аппроксимировалась выражением
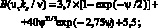
при
0,1 ≤ ψ ≤ 3,2, (2)
где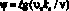 
– безразмерный комплекс.
При известном значении В(υτks/ν) по формуле (1) можно рассчитать профиль скорости и коэффициент гидравлического сопротивления. Сравнение опытных и расчетных данных по коэффициенту гидравлического сопротивления показало вполне удовлетворительное соответствие на уровне примерно 5 %, за исключением области при R/ks = 15 и Re = 4000, где расхождение возрастало до 20 %. Примечательно, что использование аппроксимационной зависимости (2) обеспечивает минимальные значения коэффициента гидравлического сопротивления, зависящее от величины безразмерной шероховатости R/ks и числа Рейнольдса Re.
В развитие такого эмпирического подхода, в работе [2], поставленная задача решалась с использованием другого подхода. Известно, что для «технической шероховатости» формула Колбрука – Уайта справедлива при всех трех режимах течения. Далее, предполагая, что функциональный вид зависимости сохранялся, была предложена обобщенная формула Колбрука – Уайта в виде зависимости
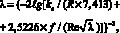(3)
где f – поправочная функция, зависящая от безразмерного комплекса (ksυτ/ν).
Проведенные параметрические расчеты показали, что удовлетворительное соответствие с опытными данными по коэффициенту гидравлического сопротивления имеет место при следующем виде поправочной функции:
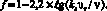(4)
В этом случае использование зависимости (1) также позволяет определять всю совокупность характеристик потока: профиль скорости и коэффициент гидравлического сопротивления. Уровень расхождения расчетных и экспериментальных значений снижается примерно в два раза, в том числе и при R/ks = 15 и Re = 4000. Такой результат представляется ожидаемым, поскольку аппроксимировалась не промежуточная величина В(υτks/ν), а конечное значение расчетной величины λ.
Зависимости (2), (3) и (4) являются эмпирическими, поэтому и соответствующие итоговые формулы относятся к зависимостям такого рода. Как любые эмпирические зависимости, они могут использоваться только в диапазоне изменения опытных данных, в том числе и для интерполяции между опытными значениями, например, при промежуточных значениях высоты элементов песочной шероховатости 0 ≤ ks ≤ 507. Однако на практике при трубопроводном транспорте внутренняя поверхность трубы, в плане шероховатости редко бывает однородной. Например, даже при перекачке воды из природных водоемов за счет донных отложений вдоль нижней образующей трубы возникает слой твердого осадка, имеющего определенную степень шероховатости. При гидротранспортировании измельченных твердых материалов по горизонтальным трубопроводам, даже при отсутствии твердого осадка вдоль нижней образующей трубы, шероховатость поверхности переменна. В нижней придонной области течения перемещаются наиболее крупные частицы, причем их объемное содержание выше, чем в среднем по потоку. В верхней части наблюдается обратная картина. В этой области перемещаются частицы мелких фракций, и их объемное содержание меньше, чем в среднем по потоку. В результате взаимодействия движущихся частиц с внутренней поверхностью трубы поверхность трубы становится шероховатой, причем шероховатость придонной части трубы выше шероховатости в верхней части трубы. В этом случае эмпирические зависимости, не учитывающие переменность шероховатости стенки трубы по высоте, могут использоваться лишь для предварительных оценок.
Для разработки методики расчета в случае поверхности с переменной шероховатостью необходимо сформулировать адекватную физико-математическую модель течения. Исходным элементом этой модели является подтверждение того, что при равномерной песочной шероховатости поверхности коэффициент гидравлического сопротивления достаточно удовлетворительно совпадает с опытными данными. На основании обзора публикаций, выполненного в работах [1, 2], представим коэффициент гидравлического сопротивления трубы с произвольной песочной шероховатостью в виде зависимости
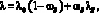(5)
где λ, λo и λs – коэффициент гидравлического сопротивления: усредненный по всей поверхности; над частью поверхности с гидравлически гладкой стенкой; над частью поверхности с полным проявлением песочной шероховатости соответственно. А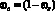 
и ωs – доли поверхности: над частью поверхности с гидравлически гладкой стенкой и над частью поверхности с полным проявлением песочной шероховатости.
В качестве зависимостей для расчета коэффициентов гидравлического сопротивления для гидравлически гладкой поверхности использовалась формула Прандтля [5]
(6)
и формула Кармана [5] при полном проявлении шероховатости
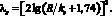(7)
Поскольку при песочной шероховатости поверхность полностью заполнена частицами, а их влияние на гидравлическое сопротивление проявляется после того, как вершины частиц выходят за пределы вязкого подслоя, то величину ωs можно определить с помощью выражения [1]
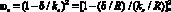(8)
где δ – толщина вязкого подслоя.
Величин безразмерной толщины вязкого подслоя определяется выражением
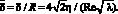(9)
В выражении (9) принималось, что зона вязкого течения η определяется выражением η = δυτ/ν = 3, как среднее значение между значениями Райхардта [1] η = 2 и Кармана [5] η = 5.
Совокупность выражений (5)÷(9) позволяет рассчитать зависимость λ = λ(Re, R/ks). Причем если ks ≤ δ, то есть элементы песочной шероховатости не выходят за толщину вязкого подслоя, то величина λ рассчитывается по формуле (6).
На рис. 1 приведены результаты сравнения опытных данных и расчета по формулам (5)÷(9).
Результаты расчетов достаточно удовлетворительно согласуются с опытными данными Никурадзе, и в том числе в области минимума значений коэффициентов гидравлического сопротивления, что практически не отражено в зависимостях других авторов.
Используя полученные таким образом расчетные значения λ, можно рассчитать величину B по формуле (1). Результаты расчетов показаны на рис. 2.
Профиль относительной расчетной скорости U/υτ в трубе с произвольной песочной шероховатостью стенки трубы определяется по известной формуле [5]
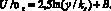, (10)
в которой величина B рассчитывалась по (1), а величина λ по (5)÷(9). Расчеты выполнялись для указанных на рис. 3 чисел Рейнольдса при различных степенях степени песочной шероховатости стенки трубы 15 ≤ R/ks ≤ 507. В качестве абсциссы использовался безразмерный параметр [3]
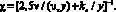
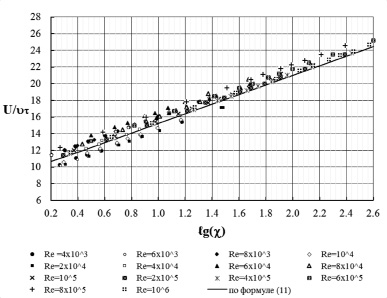
Рис. 3. Расчетные значения относительной скорости U/υτ, определенные по формуле (10), и их аппроксимация по формуле (11)
Результаты численных расчетов с погрешностью 10 % аппроксимируются зависимостью
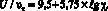(11)
Расчет профиля скорости является важной задачей, но конечной практической целью расчетных исследований, как правило, является определение коэффициентов гидравлического сопротивление, при которых использование инженерных аналитических зависимостей представляется предпочтительным.
В вычислительном плане, аппроксимация, предложенная в [2] (формулы (3), (4)), значительно упрощает процедуру расчета для однородной степени шероховатости поверхности. Соотношения, полученные в данной работе, при примерно одинаковом расхождении с опытными данными, включают физическое обоснование получаемых зависимостей и в связи с этим представляются более достоверными, что дает возможность не только для интерполяции внутри диапазона экспериментальных значений высоты песочной шероховатости 15 ≤ R/ks ≤ 507, но и экстраполяции за указанные пределы. Это также является обоснованием для проведения расчета профиля скорости над поверхностью с песочной шероховатостью, при переменной степени шероховатости поверхности, и может определять интегральный коэффициент гидравлического сопротивления в таких трубопроводах.