Изучение низкотемпературной плазмы, возникающей в атмосферных разрядах при нормальных давлениях, представляет как прикладной, так и фундаментальный интерес. В настоящее время низкотемпературная плазма атмосферных разрядов с успехом используется в медицине для стерилизации поверхностей из различных материалов, в том числе – живых тканей [6, 8]. Энергетические и химические параметры используемых плазменных факелов сравнительно легко перестраиваются в весьма широких пределах, что позволяет переводить приборы из режима щадящей обработки поверхностей в режимы разрушающего воздействия (резка тканей, коагуляция кровотечений и т.д.). Весьма перспективной представляется плазменная обработка пищевых продуктов [7]. Техническая реализация разрядов указанного типа достаточно проста и не требует уникального оборудования. В то же время экспериментальное исследование параметров плазм возникающих в факелах атмосферных разрядов весьма нетривиально. Последнее связано с малыми геометрическими размерами и короткими временами существования последних. В этой связи особо важное значение принимает корректное численное моделирование используемых в технических устройствах разрядов с целью понимания физики протекающих в них процессов и оптимизации параметров, возникающих в них плазм.
Цель исследования
Целью работы является изучение особенностей коронного и искрового разряда в струе аргона, создаваемого серийно выпускаемым медицинским аппаратом «Аппарат электрохирургический высокочастотный с двумя режимами аргоноплазменной коагуляции ЭХВЧАрК-120-01-ЭФА-М» (далее АЭХВАК). Выполняемое исследование, с одной стороны, ориентировано на разработку методов управления плазменными параметрами с целью их оптимизации и перестройки при решении различных задач практической хирургии и плазменной терапии, с другой – представляет определенный фундаментальный интерес, как пример изучения весьма экзотического класса разрядов, позволяющего протестировать развиваемые методы моделирования нелокальной плазмы на системах существенно отличающихся от используемых при развитии этих численных методов.
Материалы и методы исследования
Для проведения работы был создан эксклюзивный вариант устройства АЭХВАК, ориентированный на экспериментальное изучение генерируемого им плазменного факела (рис. 1). Данный вариант отличается более гибкой системой настроек и возможностью автоматизации их изменения с помощью программных сред для автоматизации экспериментов. Схема установки имела следующие параметры: длина трубки-сопла может варьироваться в пределах от 50 мм до 300 мм, рабочее значение – 100 мм. Внутренний диаметр самой трубки 3 мм. На оси трубки находится электрод-игла диаметром 0,5 мм. Расстояние до второго электрода («ткани пациента») – порядка 10 мм (допустимый диапазон от 5 мм до 25 мм). В экспериментальном варианте в качестве второго электрода используются сменные насадки из металла: плоский диск, полусфера, коническая поверхность со сферическим закруглением при вершине. Использование металлического электрода-«пациента» позволяет увеличивать время экспозиции без повреждения электрода.
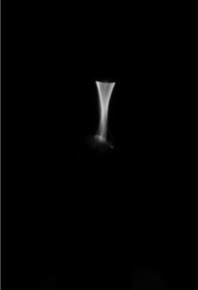
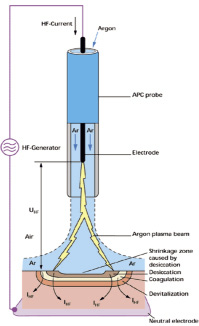
Рис. 1. Экспериментальный вариант хирургического инструмента «плазменное перо» и создаваемый им плазменный факел
Устройство допускает возможность варьирования химического состава прокачиваемого газа (все инертные газы и их калиброванные смеси; инертные газы с добавками азота, кислорода, атмосферного воздуха). В рамках эксперимента наибольший интерес представляют аргон, в силу его повсеместной распространенности, и криптон, в силу его сравнительной доступности, но потенциально большей эффективности. Объёмные расходы инертного газа стабилизируются и могут варьироваться в пределах от 0,5 до 10 л/мин (рабочий объёмный расход 3,5 л/мин). Давление газа в струе внутри трубки контролируется специальным датчиком. Для создания разряда используется импульсный генератор плазмы, длительность импульса 1 мкс. На генератор плазмы подается последовательность таких импульсов с частотой повторения от 10 до 100 кГц (рабочее значение 30 кГц). Амплитуда импульса может достигать 3 кВ. Два разделительных конденсатора имеют ёмкость 1000 пФ, они включены в каждый полюс источника, т.е. последовательно. Роль отсутствующего балластного резистора играет внутреннее сопротивление генератора (200-300 Ом) и второй электрод («ткань»).
Модель тлеющего разряда в струе криптона разработана с помощью комплекса моделирующих программ, в качестве ядра которого выступают два модуля среды COMSOL [5]. Плазмохимическая модель разряда строилась аналогично ранее описанным моделям в [3, 4]. Малые длительности импульсных разрядов при реализуемых скоростях газа на срезе сопла позволили использовать квазистатическое приближение. В его рамках расчет разряда в струе осуществлялся в два этапа. На первом решалась двумерная аэродинамическая задача расчета пространственного распределения давлений и концентраций атомов инертного газа в струе, инжектируемой в неподвижный воздух при нормальном давлении. На втором этапе осуществлялось моделирование тлеющего разряда в статическом распределении смеси воздуха и аргона.
Расчёт в рамках «микроскопического усредненного» подхода, позволяющего осуществлять индивидуальный учет элементарных процессов в газоразрядных средах на базе гидродинамического приближения, осуществляется в 2 этапа. На первом этапе находится функция распределения при помощи решения уравнения Больцмана или аналитическая полуэмпирическая модель газоразрядного промежутка. Результатом решения являются зависящие от двух переменных (E и ne) значения функции распределения электронов по энергиям (ФРЭ). На основе ФРЭ вычисляется температура электронов, коэффициенты скоростей реакций, а также коэффициенты переноса (диффузии и подвижности электронов) как функции от напряженности поля и концентрации.
На втором этапе полученное в нулевом приближении «стартовое» решение уточняется методом последовательных приближений. В ходе каждой итерации решается система уравнений типа (1–5), в которой учитываемый набор частиц и список задающих конкретный вид этих уравнений элементарных процессов и плазмохимических реакций определяется пользователем в соответствии с формулируемой им физической моделью.
Для описания временной эволюции концентраций каждого типа частиц j в газовом разряде используются дифференциальное уравнение, выражающее, по сути, соответствующие законы сохранения:
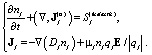 (1)
(1)
Сходное уравнение, выражающее закон сохранения энергии, записывается для объемных плотностей энергий для каждого из сортов частиц:
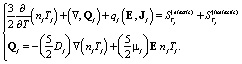 (2)
(2)
В соотношениях (1) и (2) через Jj и Qj обозначены соответственно плотности потоков числа частиц и связанных с ними тепловых энергий, возникающих в результате процессов диффузии (Dj – коэффициент диффузии) и дрейфа под действием сил поля (μj -подвижность). Через Sj обозначены объемные плотности скоростей реакций рождения и гибели частиц каждого сорта при столкновениях, а также скоростей выделения и поглощения связанной с этими частицами тепловой энергии. Эти скорости пропорциональны концентрациям рассматриваемых частиц. Так, например, в случае учета реакций, протекающих при двухчастичных столкновениях, выражение для такой скорости имеет вид
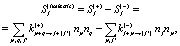 (3)
(3)
где через kpq обозначены константы скоростей реакций, приводящих к рождению и гибели частиц рассматриваемого сорта. Такие константы вычисляются, исходя из сечений элементарных столкновительных процессов σpq и функции распределения f по скоростям относительного движения частиц, участвующих в элементарном процессе:
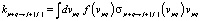 . (4)
. (4)
Константы скоростей прямых и обратных двухчастичных столкновительных процессов и соответствующие сечения связаны между собой известными соотношениями, вытекающими из требования возможности нахождения сиcтемы в состоянии термодинамического равновесия при температуре Т:
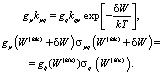
В двух последних формулах индексы q и p нумеруют состояния участников элементарного столкновительного процесса до и после взаимодействия, gq и gp – статистические веса соответствующих состояний, W(kin) – кинетическая энергия относительного движения сталкивающихся частиц, δW – энергия, передаваемая при неупругом столкновении.
Для получения замкнутой задачи описания системы уравнения (1–4) дополняются известными из электродинамики уравнениями для квазистатического электрического поля:
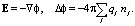 (5)
(5)
Помимо проблем чисто вычислительного характера (учет гигантского числа типов взаимодействующих и превращающихся друг в друга частиц) задача осложнена рядом носящих принципиальный характер физических проблем. К этим проблемам относятся: алгоритмы ограничения набора учитываемых элементарных процессов и числа квантовых состояний атомов, молекул и их ионов, необходимость наличия информации о функциях распределения по скоростям и зависимостях констант скоростей элементарных процессов от энергий (или зависимостей соответствующих сечений от относительных скоростей).
При этом значения зависящих от функции распределения электронов коэффициентов переноса и констант скоростей реакций берутся из решений, полученных в ходе предшествующей итерации. Таким образом, найденные функции распределения вводятся в систему (1–5) неявно, в виде вычисленных с их помощью констант скоростей реакций (3). На каждой итерации система дифференциальных уравнений в частных производных решается стандартными методами, реализованными в плазменном модуле моделирующей среды COMSOL. После решения системы уравнений (1–5) осуществляется корректировка пространственного распределения электронной температуры и концентрации носителей зарядов, пересчитываются зависящие от этих параметров коэффициенты и осуществляется переход к следующей итерации.
Упрощенная схема алгоритма решения самосогласованной задачи моделирования нелокальной плазмы приведена на рис. 2.
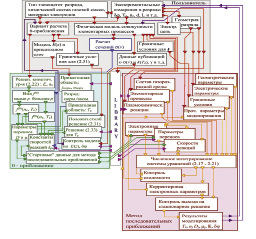
Рис. 2. Упрощенный алгоритм автоматизированного расчета параметров нелокальных газоразрядных сред с использованием плазменного модуля моделирующей оболочки
На приведенной схеме красными стрелками показаны действия пользователя по постановке задачи и выбору приближений для ее решений; зелеными – первый этап решения, состоящий в получении стартового приближения для запуска расчета по методу последовательных приближений; розовыми – дополнительная информация, получаемая из литературных источников; оранжевыми – основной расчет, основанный на решении системы «гидродинамических» уравнений в частных производных; синими – данные, получаемые в результате квантовомеханических расчетов сечений элементарных процессов; фиолетовыми – осуществляемый пользователем контроль промежуточных и конечных результатов.
Приведенный алгоритм, по сути, реализует гибридный подход к моделированию плазмы, сочетающий преимущества гидродинамических и кинетических моделей. В гидродинамических моделях характеристиками компонент плазмы (электроны, ионы, нейтралы) являются такие макроскопические параметры, как концентрации, потоки, средняя энергия частиц. Изменения этих характеристик в пространстве и во времени описываются гидродинамическими уравнениями баланса. Поскольку частицы имеют заряд, для описания их взаимодействия с электрическим полем, система решается совместно с уравнениями Максвелла (в том числе с уравнением Пуассона).
На приведенной заведомо упрощенной схеме не нашла отражения процедура выбора сетки для решения системы дифференциальных уравнений. При решении задач описания стационарной плазмы сетка задавалась вручную с учетом геометрии разрядного промежутка и иных априорных физических соображений. При переходе к решению задач описания существенно нестационарных газоразрядных сред и протекающих в них процессов было признано целесообразным автоматизировать эту часть работ по моделированию. В результате был осуществлен переход к адаптивным методам построения сетки, параметры которой менялись в ходе решения задачи. Новый подход был успешно апробирован в ходе моделирования пробоя в гелии [1] и показал свою работоспособность.
При постройке подобной сложной интегральной модели необходимо правильно учесть взаимодействия между плазменной и гидродинамической системой. Очень важно правильно выбрать сетку для расчётов, т.к. гидродинамика требует очень точкой сетки, но при этом серьёзно возрастает время расчёта реакций в плазме, поэтому важно задать для каждого свою сетку. Так же при моделировании заряда должно учитываться давление, получаемое из распределения скоростей, рассчитанного в гидродинамике. Задача же граничных условий является одной из самых важных при подобных расчётах. Необходимо, чтобы они полностью сочетались между собой, не внося противоречий в систему, иначе полученный результат будет не консистентным. И так как расчёты данной модели даже на современных вычислительных устройствах могут занимать значительное время (в условиях одновременной вариации параметров для установления различных зависимостей), то необходимо максимально воспользоваться возможностью создания границ симметричности, за счёт чего возможно в разы повысить скорость расчёта модели.
Использовалась стандартная плазмохимическая модель аргона из [5], учитывающая только один эффективный возбужденный уровень. Для воздуха, в соответствии с результатами ранее выполненных сравнений модельных расчетов с плазменным экспериментом [2], использовалась модифицированная модель разряда в аргоне с измененными параметрами, описывающими потери энергии электронов при столкновении с частицами газа и вероятностями выбивания электронов с катода при его ионной бомбардировке. Таким образом плазмохимическая модель объединяла две 2D-модели, развитые и оптимизированные для тлеющих разрядов в аргоне и воздушной смеси при пониженных давлениях без учета элементарных столкновительных процессов между частицами из различных подсистем. Газодинамическая часть модели строилась в предположении о слабой турбулентности потоков.
Результаты исследования и их обсуждение
Результаты моделирования приведены на рис. 3. Результаты моделирования электрических параметров разрядного промежутка и пространственного распределения возбужденных атомов согласуются с усредненными по времени характеристиками серии импульсных квази искровых разрядов.
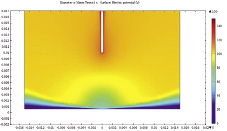


Рис. 3. Результаты моделирования импульсного тлеющего разряда в струе аргона, инжектируемого в воздух (приведены 2D-распределения: потенциала, электронной плотности, электронной температуры; масштаб по горизонтали существенно увеличен для удобства восприятия)

Рис. 4. Фотография разрядов, сделанная с помощью высокоскоростной камеры
Заключение
Результаты моделирования с хорошей точностью совпадают с экспериментом, поэтому можно переходить к моделированию более сложных сценариев. Отдельный интерес представляет моделирование разряда при максимальных скоростях газа, так как поток становится существенно неламинарным и треки отдельных импульсов перестают быть ровными (рис. 4). Газодинамическая часть разработанной модели построена в предположении о слабой турбулентности потоков и квазистационарности разрядов. Детальное моделирование отдельных импульсных разрядов со стохастически изменяющимися пространственными конфигурациями требует перехода к динамическим 3D-моделям разрядного промежутка, учитывающим взаимодействия между рассматриваемыми описанными подсистемами. Построение и отладка нового варианта численной модели осуществляется путем создания вспомогательных компьютерных симуляций для упрощенных условий, подбираемых так, чтобы в соответствующей оптимизируемой подмодели процесс играл по возможности доминирующую роль. В случаях, когда оказывается осуществимым надежный экспериментальный контроль параметров плазмы соответствующих упрощенным вариантом разрядов, осуществляются проверка и дополнительная настройка в соответствии с приближениям вспомогательных моделей и их включение в разрабатываемую интегральную модель реального устройства, представляющего собой весьма сложную физико-химическую систему.
В дальнейшем также предстоит перейти к органическим материалам в качестве второго электрода. Предстоит установить, каков механизм влияния плазмы на ткани пациента, с тем чтобы можно было продолжать совершенствовать данную технологию.



