Для расчетов адсорбции компонентов бинарных систем А–В, где А и В – компоненты системы, используют уравнение Гиббса [1]:
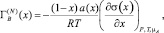 (1)
(1)
где х – термодинамическая концентрация; а(х) – термодинамическая активность компонента В; σ(x) – функция изотермы поверхностного натяжения (ПН).
Часто функции а(х) и σ(x) оказываются неизвестными. Изотерму σ(x) можно построить экспериментально, измерив ПН около полутора десятка приготовленных расплавов системы А–В, равномерно распределенных по составу в области 0 ? х ? 1.Установить функциональную зависимость термодинамической активности второго компонента В от состава расплава a(х) сложнее. Поэтому от выражения (1), при условии a(х) = γix, γi = 1 (приближение идеальных расплавов), переходят к
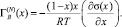 (2)
(2)
Для вычисления величины 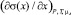 можно использовать уравнение изотермы ПН, предложенное в [2]:
можно использовать уравнение изотермы ПН, предложенное в [2]:
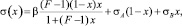 (3)
(3)
где β и F – параметры уравнения (3) и постоянные для рассматриваемой системы; σA и σB – ПН чистых компонентов А и В системы А–В.
В [3] показано, что уравнение (3) описывает экспериментальные изотермы ПН с высокой точностью и может быть использовано для расчета величины 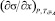 , которая необходима для расчета адсорбции по (2).
, которая необходима для расчета адсорбции по (2).
Оценка величины адсорбции компонентов в приближении идеальных растворов
Продифференцировав (3) по х и подставляя полученное выражение в (2), было получено [2]
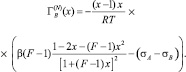 (4)
(4)
Формула (4) значительно уменьшает ошибки, допускаемые при графическом дифференцировании экспериментальной кривой, однако она позволяет вычислить адсорбцию в приближении идеального раствора (γi = 1).
Расчет адсорбции компонентов в приближении реальных растворов
Чтобы приблизиться к данным для реальных растворов, в [4] было предложено вычислить адсорбцию второго компонента бинарной системы А–В с использованием определения адсорбции в N – варианте Гуггенгейма-Адама [1]:
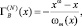 (5)
(5)
где [5]
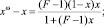 (6)
(6)
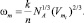 (7)
(7)
В (7) Vm(x) – молярный объем раствора состава х, который определим как
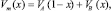 (8)
(8)
где VA и VВ – молярные объемы компонентов А и В. Результаты расчетов будут точнее, если использовать экспериментальные Vm(x). В наших расчетах принято k и n = 1.
Для определения параметров β и F уравнения (3) перепишем в виде [3]
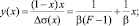 (9)
(9)
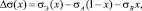 (10)
(10)
где sэ(х) – ПН расплава состава х, определенное в эксперименте. Очевидно, что можем вычислить величину 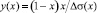 из данных эксперимента. Тогда, построив график функции y(х), будем иметь прямую (9), наклоненную к оси х под углом a. Продолжив прямую до пересечения с осью OY, определим отрезок, равный
из данных эксперимента. Тогда, построив график функции y(х), будем иметь прямую (9), наклоненную к оси х под углом a. Продолжив прямую до пересечения с осью OY, определим отрезок, равный
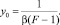 (11)
(11)
Угол наклона прямой (9) к оси OX определяет величину b:
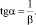 (12)
(12)
Решив совместно (11) и (12), найдем значения b и F для данной системы.
Очевидно, что если эксперимент по изучению изотермы ПН дает прямую линию (см. (9)), то уравнение (3) для данной системы справедливо и может быть использовано для расчетов адсорбции компонентов по (4) – в приближении идеальных растворов и по (5)–(8) – для расчетов адсорбции компонентов в приближении реальных растворов. Действительно, расчет адсорбции висмута в хорошо изученной системе Pb–Bi по формулам (1), (4) и (5)–(8) [6] показал хорошее совпадение данных, полученных по (1) и (5)–(8) (рис. 1).
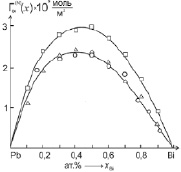
Рис. 1. Результаты расчетов адсорбции висмута в расплавах системы Pb-Bi по [6]: ? – в приближении идеального раствора по (2); о – с учетом термодинамической активности по (1); Δ – по формуле (4)
Как видно из сравнения результатов (рис. 1), второй способ расчета адсорбции (4) дает данные, более близкие к реальным. Итак, второй способ может быть использован для расчетов адсорбции компонентов расплавов бинарных систем в случае монотонного изменения ПН в зависимости от состава. Представляет определенный интерес применить этот метод к системам, в которых компоненты образуют устойчивые химические соединения типа AmBn.
При вычислениях изотерм адсорбции 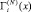 (i = A и В) компонентов А и В уравнения (2) и (3) применяют ко всей области определения расплавов бинарных систем А–В (0 ? х? 1), что справедливо, когда компоненты системы не склонны образовывать устойчивые химические соединения типа АmBn. В противном случае, то есть, при образовании компонентами устойчивых химических соединений АmBn, систему разбивают на вторичные А–АmBn и АmBn–B [7] и к каждой вторичной системе применяют уравнения (2) и (3). Такая методика расчета адсорбции компонентов системы А–В позволяет нам выяснить роль устойчивых молекул АmBn в формировании свойств поверхностей расплавов системы А–В. Однако при этом вычисления адсорбции компонентов проводят в приближении идеальных растворов. Для приближения результатов расчетов к реальным значениям в [7] разработана методика, позволяющая получить более достоверные данные. Здесь показано, что при вычислениях адсорбции компонентов системы А–В, в которых компоненты образуют химические соединения АmBn, необходимо переходить к приведенным концентрациям:
(i = A и В) компонентов А и В уравнения (2) и (3) применяют ко всей области определения расплавов бинарных систем А–В (0 ? х? 1), что справедливо, когда компоненты системы не склонны образовывать устойчивые химические соединения типа АmBn. В противном случае, то есть, при образовании компонентами устойчивых химических соединений АmBn, систему разбивают на вторичные А–АmBn и АmBn–B [7] и к каждой вторичной системе применяют уравнения (2) и (3). Такая методика расчета адсорбции компонентов системы А–В позволяет нам выяснить роль устойчивых молекул АmBn в формировании свойств поверхностей расплавов системы А–В. Однако при этом вычисления адсорбции компонентов проводят в приближении идеальных растворов. Для приближения результатов расчетов к реальным значениям в [7] разработана методика, позволяющая получить более достоверные данные. Здесь показано, что при вычислениях адсорбции компонентов системы А–В, в которых компоненты образуют химические соединения АmBn, необходимо переходить к приведенным концентрациям:
для А–Аm Bn
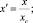 (13)
(13)
и для Аm Bn–В
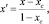 (14)
(14)
где хс – концентрация, определяющая состав химсоединения АmBn.
После расчетов адсорбции компонентов в системе x′ результаты следует обратно перевести в систему нормальных концентраций х второго компонента В по формулам (13) и (14).
Ниже, в качестве примера рассмотрим расчет адсорбции компонентов бинарных систем Al-La и Al-Nd, в которых образуются устойчивые при температурах измерения ПН химические соединения Al2La и Al2Nd.
Изотермы ПН бинарных систем Al-La и Al-Nd
На рис. 1 и 2 представлены изотермы ПН бинарных систем Al-La и Al-Nd, построенные в [8] при температурах 1773 К. Эти изотермы отличаются от рассмотренных в [3] тем, что первые части их (до химсоединений) находятся выше аддитивной прямой, тогда как остальные части изотерм ПН, как и в [3], находятся ниже аддитивной прямой (рис. 2 и 3).
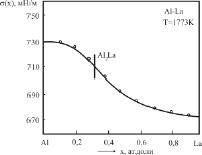
Рис. 2. Изотермы ПН бинарных систем Al-La: o – эксперимент [8]; – – расчет по (3)
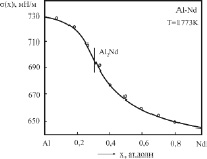
Рис. 3. Изотерма ПН бинарных систем Al-Nd: o – эксперимент [8]; – – расчет по (3).
Результаты экспериментов [8] нами обработаны по методике [3], построены теоретические изотермы по (3) (см. сплошные линии на рис. 2 и 3), и найдены параметры b и F уравнения (3) для каждой вторичной системы Al-Al2La и Al2La-La; Al-Al2Nd и Al2Nd-Nd (табл. 1).
Результаты расчетов адсорбции компонентов систем Al-La и Al-Nd
Результаты наших расчетов адсорбции молекул Al2La, Al2Nd и металлов La и Nd в расплавах бинарных систем Al-La и Al-Nd представлены на рис. 4 и 5.
Таблица 1
Входные данные для расчетов bi и Fi и их значения
|
№ п/п |
Система |
Вторичная система |
sA, мН/м |
sB, мН/м |
bi, мН/м |
Fi |
|
1. |
Al-La |
Al-Al2La |
731 |
710 |
91 |
1,24 |
|
Al2La –La |
710 |
670,5 |
–55,5 |
2,63 |
||
|
2. |
Al-Nd |
Al-Al2Nd |
731 |
690 |
100 |
1,63 |
|
Al2Nd-Nd |
690 |
645 |
–41,6 |
3,82 |
Таблица 2
Входные данные для расчетов ωm для систем Al-La и Al-Nd
|
Система |
МA•103, кг/моль |
МB•103, кг/моль |
rA, кг/м3 |
rB, кг/м3 |
wA•10–4, м2/моль |
wB•10–4, м2/моль |
|
Al-La |
26,98 |
138,91 |
2700 |
6162 |
3,9 |
6,7 |
|
Al-Nd |
26,98 |
144,24 |
2700 |
7007 |
3,9 |
6,3 |
Здесь следует иметь в виду, что адсорбция растворителя равна адсорбции добавляемого в раствор компонента, взятой с противоположным знаком.
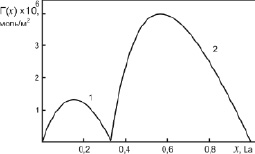
Рис. 4. Адсорбция компонентов бинарной системы Al-La: 1 – адсорбция молекул Al2La; 2 – адсорбция атомов La на поверхности жидкого химсоединения Al2La
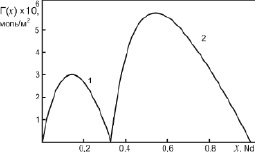
Рис. 5. Адсорбция компонентов бинарной системы Al-Nd: 1 – адсорбция молекул Al2Nd; 2 – адсорбция атомов Nd на поверхности жидкого химсоединения Al2Nd
Как видно из рис. 4 и 5, молекулы химсоединений Al2La и Al2Nd проявляют поверхностную активность в области 0 < х < 0,33. При этом молекулы Al2Nd являются более поверхностно активными, чем Al2La по отношению к алюминию. В области 0,33 < х < 1 на поверхности расплавленных химсоединений Al2La и Al2Nd выходят атомы чистых металлов La и Nd, а молекулы Al2La и Al2Nd проявляют поверхностную инактивность по отношению к La и Nd.
Выводы
1. Предложена методика расчета адсорбции компонентов бинарных расплавов системы А–В, компоненты которых образуют устойчивые при температурах измерений поверхностного натяжения химические соединения типа АmBn.
2. На примерах бинарных систем Al-La и Al-Nd показано, что молекулы Al2La и Al2Nd могут значительно повлиять на ход изотерм адсорбции La и Nd.
3. Оказалось, что молекулы Al2La и Al2Nd ведут себя как поверхностно активные по отношению к алюминию в области 0 < х < 0,33 и поверхностноинактивные по отношению к La и Nd при х > 0,33.



