Надежность работы сложных технических систем с модулями автономного питания в значительной степени зависит от текущего состояния и согласованности работы отдельных элементов батарей химических источников тока (ХИТ), обеспечивающих их бесперебойное функционирование. Благодаря эксплуатационным параметрам, таким как ресурс, нагрузочная способность, температурный диапазон и др., во многих подобных системах в качестве ХИТ используются батареи никель-кадмиевых аккумуляторов. Существующие способы использования аккумуляторных батарей требуют для повышения надежности и срока службы осуществлять постоянный контроль основных электрических параметров аккумуляторов (АК).
При эксплуатации АК, на ряду с остаточной емкостью Qост, большое значение имеют его сопротивление по переменному току, сопротивление по постоянному току и активационная емкость. Сопротивление по переменному току R определяет максимальный ток АК при подключении нагрузки. Сопротивление по постоянному току состоит из последовательно включенных сопротивлений по переменному току и активационного Rа и определяет максимальный ток АК в установившемся режиме. Активационная емкость Са определяет длительность переходного процесса в АК в динамических режимах работы. Указанные параметры со временем изменяются (ухудшаются) быстрее, чем номинальная емкость АК Qном. Зачастую именно они делают невозможным эксплуатацию АК при больших токах нагрузки.
Как правило, эти параметры нельзя определить выполнением прямых измерений. Для решения задачи целесообразно проведение натурно-модельного эксперимента, в результате которого выполняется анализ сигнала отклика АК на электрическое воздействие определенной формы. Определение параметров аккумуляторов по полученному сигналу отклика относится к классу обратных задач электротехники [1]. Разработан метод решения обратной задачи диагностики параметров никель-кадмиевых аккумуляторов (НКА) для систем оперативного контроля, включающий проведение натурно-модельного эксперимента с использованием потенциостатических испытаний, основанных на активном импульсно-релаксационном принципе [3–5, 9]. Этот принцип заключается в исследовании реакции системы на потенциостатические воздействия. Как было показано в [3, 5] потенциостатическое воздействие является наиболее информативным по сравнению с другими существующими воздействиями, так как оно обеспечивает существенные изменения протекающего через аккумулятор анализируемого тока при незначительном изменении напряжения на зажимах АК. На рис. 1, а и б показаны графики напряжения и тока при потенциостатическом воздействии соответственно.
Для реализации метода решения обратной задачи диагностики указанных параметров предложена комплексная адаптивная модель редукции измерений (рис. 2), содержащая следующие части:
– модель понижения размерности графика тока отклика Iакк для уменьшения пространства измеренных параметров путем исключения шумовых и неинформативных составляющих;
– регрессионную модель пониженной размерности для определения остаточной емкости АК Qост по образам зависимостей откликов;
а
б
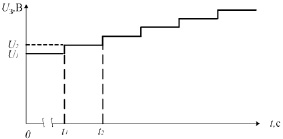
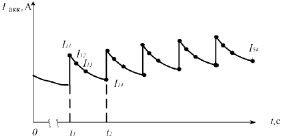
Рис. 1. Зависимости потенциостатического напряжения Uз (а) и тока Iакк (б): U1 – буферное напряжение АК; U2 – напряжение АК при первом потенциостатическом воздействии; t1 – время начала первого потенциостатического воздействия; t2 – время начала второго потенциостатического воздействия; 
– измеренные значения токов отклика Iакк
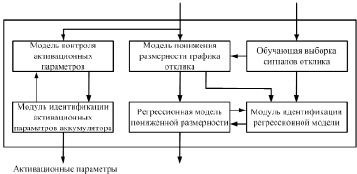
Рис. 2. Комплексная адаптивная модель редукции измерений и оценки параметров АК: {Ii(t), Qi} – обучающая выборка значений токов отклика Iакк и известных значений остаточной емкости Qост;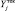 
– образ графика зависимости тока отклика от времени; Yi – образы графиков зависимостей токов откликов обучающей выборки; 
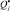– расчетные значения остаточной емкости Qост
– модель контроля активационных параметров для нахождения взаимосвязи измеренных и внутренних (модельных) активационных параметров АК;
– модуль идентификации регрессионной модели, для параметрической идентификации выбранной регрессионной модели определения остаточной емкости Qост;
– модуль идентификации активационных параметров для параметрической идентификации модели активационных параметров;
– обучающая выборка или конечное множество сигналов эталонных токовых откликов Iакк с известными параметрами АК (в частности, текущая емкость и активационные параметры).
Последние три части модели реализуются стандартными средствами регрессионного и компонентного анализов [7].
Модель понижения размерности графика отклика используется для уменьшения размерности пространства измеренных параметров путем исключения шумовых и неинформативных составляющих на основе декомпозиционных подходов [5, 7, 8].
Декомпозиция используется при моделировании сложных технических систем путем замены исходного объекта более простыми объектами, его составляющими, с заданной точностью. Эффективность декомпозиции ярко выражена в тех случаях, когда применение традиционных подходов к решению задачи представляет большую сложность [6, 7].
НКА является сложной динамической системой, которая обладает достаточно большой размерностью входных измеренных и выходных контролируемых параметров. Качественно НКА представляется нелинейной системой, которая имеет неопределенности в описании математической модели. Поэтому при решении обратной задачи диагностики НКА возникает необходимость в преобразовании исходных измеренных данных и упрощении как исходной математической модели, так и первоначальной постановки задачи, используя декомпозиционный метод моделирования [5, 7] для выявления скрытых зависимостей.
С целью получения исходной выборки строится матрица разброса графиков, и определяются ее собственные векторы. Такое преобразование позволяет трансформировать графики с большим числом отсчетов в малоразмерный образ с минимальной потерей информативности. Модель понижения размерности, построенная на данном принципе, обеспечивает существенное уменьшение пространства моделирования, а следовательно, повышает вычислительную устойчивость регрессионной модели и процесса идентификации.
При построении регрессионной модели пониженной размерности в устройстве контроля используются полученные образы графиков откликов.
Для разработки модели контроля активационных параметров выполнялись исследования существующих моделей АК. Выделены два типа моделей: моделирующие «быстрые» переходные процессы в АК (с учетом активационных параметров) и моделирующие «медленные» процессы, связанные с основной токообразующей цепью. Следовательно, для эффективной оценки параметров АК необходимо построить комбинированную модель, учитывающую особенности моделей.
В качестве модели «быстрых» переходных процессов использовалась уточненная для потенциостатических испытаний модель проф. К.В. Безручко [2], обобщенно представляемая схемой замещения АК (рис. 3).
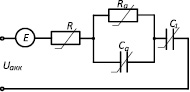
Рис. 3. Схема замещения аккумулятора: E – идеальный источник постоянной ЭДС; R – сопротивление электролита в межэлектродном пространстве; Rа, Cа – элементы активационного блока; C1 – главный конденсатор, соответствующий основной токообразующей электрохимической реакции
Параметры АК в процессе заряда и разряда изменяются, однако при каждом потенциостатическом воздействии Uп их можно считать неизменными. Напряжение на основной токообразующей емкости изменяется гораздо медленнее, чем на активационной емкости, поэтому можно записать
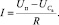
Дифференциальное уравнение для нахождения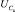 
имеет вид
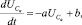(1)
где
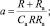
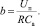
Разрешая уравнение (1) относительно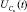 
при выполнении условия 
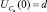, получим
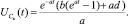(2)
Потенциостатические включения вызывают переходные процессы, обусловленные активационными явлениями в аккумуляторе. По истечении некоторого времени влияние переходного активационного процесса ослабевает, и основным процессом становится обусловленный разрядом емкости C1 процесс, зависящий от остаточной емкости аккумулятора.
Используя выражение (2), по экспериментальным измерениям тока отклика определяются значения параметров элементов R, Ra и Caсхемы замещения. Для этого достаточно реализации только одного включения. Чтобы учесть нелинейный характер, измерение осуществляется для каждой из ступеней потенциостатического воздействия. Ток в цепи АК при первом потенциостатическом включении после несложных преобразований (2) вычисляется по формуле
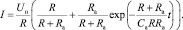
Сопротивление по переменному току определяется при t = 0, а активационные параметры находятся из системы нелинейных уравнений:
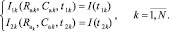
В правой части подставляются значения тока, полученные предложенным методом диагностики. В системе уравнений N – число потенциостатических воздействий.
Разработанный метод решения обратной задачи диагностики НКА экспериментально проверялся при испытаниях АК различных типов и номиналов (KR-600-AAj, GP-600, KR-1000-AAJ, GP-1000, KR-2000-SC, KR-3000-C, KR-5000-D).
Испытания АК проводились при следующих условиях: Uп = 0,01 В; значения токов измерялись через 0, 3, 6 и 10 с. после потенциостатического включения. Искомые значения параметров АК определялись для остаточных емкостей АК, равных 100, 95, 90, 85, 70, 60, 50, 40, 30, 20, 15, 10 и 5 процентов от полной емкости. Результаты определения Са и Rа для АК KR-1000-AAJ приведены на рис. 4 и 5.
Анализ полученных результатов показал, что постоянная времени RaСа практически не зависит ни от типа АК и его номинала, ни от остаточной емкости и находится в пределах от 4 до 8 с. Параметры АК изменяются в зависимости от его остаточной емкости. Наилучшие (наименьшие) значения R и Ra имеют место в средней части рабочего диапазона остаточной емкости. В этом же диапазоне обеспечиваются наилучшие (наибольшие) значения Са.
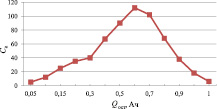
Рис. 4. Результаты определения активационной емкости Са
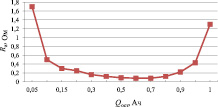
Рис. 5. Результаты определения активационного сопротивления Rа
Выводы
Анализ методов измерения параметров НКА показал, что определение сопротивления по переменному току, сопротивления по постоянному току и активационной емкости в результате прямых измерений невозможно. Разработан метод решения обратной задачи диагностики параметров никель-кадмиевых аккумуляторов, позволяющий решить эту проблему. Метод основан на проведении натурно-модельного эксперимента. Для его реализации построена адаптивная модель редукции измерений. Исследования показали, что зависимости активационных параметров от емкости АК имеют неустойчивый и изменяющийся характер. Предложенная модель дает более точную оценку этих параметров. Погрешность оценки в большей степени зависит от точности измерения потенциостатического тока, и, как показал анализ чувствительности для оценки Ra и Ca с относительной погрешностью не более 7 %, ток должен измеряться с погрешностью менее 2 %. Применение метода решения обратной задачи диагностики параметров НКА для систем оперативного контроля позволяет эффективно определять активационные параметры НКА, имеющие важное значение для исследования переходных режимов, а также для использования при комплектовании батареи.
Результаты работы получены при поддержке проекта № 1.2690.2014/K «Методы решения обратных задач диагностики сложных систем (в технике и медицине) на основе натурно-модельного эксперимента», выполняемого в рамках проектной части государственного задания и Российского фонда фундаментальных исследований (грант 15-08-08352).