Иностранным гражданам, стремящимся получить высшее образование в российских вузах, предлагается на первом этапе обучения пройти годичный курс подготовительного отделения Томского политехнического университета (ТПУ). После освоения учебного плана выбранного профиля они могут продолжить обучение по программам бакалавриата или магистратуры /аспирантуры.
Основная цель обучения на подготовительном отделении – освоение иностранными гражданами русского языка до уровня В1 и профильных дисциплин, что позволит им в дальнейшем пройти обучение по основным образовательным программам.
В настоящее время иностранным слушателям ТПУ предлагаются дисциплины по пяти профилям: экономическому, техническому, гуманитарному, медико-биологическому и естественнонаучному.
Преподаватели, обучающие иностранных студентов, постоянно совершенствуют методику преподавания на неродном языке. Например, О.В. Янущик [9] во время конференц-недель предлагает иностранным студентам подготовить доклады и выступить на русском языке по обзорным темам математики. Н.А. Соловьёва и Н.С. Полякова [5] используют междисциплинарность как метод интерактивного обучения, другие преподаватели сопровождают занятия визуализированными объектами [4, 7], либо проводят занятия в форме игры [6, 8], либо используют для организации самостоятельной работы обучающую среду Moodle [2].
Авторами в статье представлена методика проведения аудиторных занятий с иностранными слушателями, изучающими математику на русском языке как иностранном.
Заметим, что, поступив на первый курс бакалавриата, иностранные студенты в потоках с русскими студентами на занятиях по математике (и другим дисциплинам) слушают лекции и занимаются на практических занятиях на русском языке. Приём преподавателями у иностранных студентов зачетов, коллоквиумов и экзаменов также осуществляется на русском (неродном) языке.
Поэтому цель нашего исследования заключается в формировании у иностранных слушателей языковой компетенции по предмету в ходе организации аудиторных и внеаудиторных занятий по математике.
Авторами разработаны задания пяти типов, работа над которыми направлена на формирование у иностранных слушателей владения формами устной речи и математической лексикой на русском языке.
Рассмотрим методику работы с разработанными типами заданий на занятии по математике с иностранными слушателями подготовительного отделения.
1. Задание по образцу.
Часть упражнений преподаватель формулирует методом образцов. Например, рассмотрим тему «Делимость чисел». При изучении темы сначала обучающиеся изучают на русском языке понятия делителя, кратного, простого и составного чисел, а также разложение чисел на простые множители, нахождение наименьшего общего кратного и наибольшего общего делителя. Рассмотрим задание по образцу на запоминание терминов «простое число» и «составное число».
Задание. Определите, число а – простое или составное число? Объясните ответ.
Образец: Число 66 – это составное число, потому что число 66 делится на 2, на 3, на 11, на 22, на 33, на 1 и на себя.
Число 5 – это простое число, потому что число 5 делится только на 1 и на себя.
Далее иностранным слушателям предлагается самостоятельно выполнить 8–12 подобных заданий.
2. Задание – анализ текста.
Задания второго типа разделены на три типа. Обучающимся предлагается сначала прочитать новый текст на русском языке, затем:
1) в тексте вставить пропущенные слова, которые встречались в новом тексте;
2) составить вопросы к этому тексту;
3) ответить на вопросы, предложенные преподавателем или студентами.
Приведем пример задания второго типа.
Задание. Прочитайте текст.
Проекцией вектора 
на вектор 
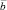называется число, равное произведению модуля вектора 
на косинус угла между ними.
Проекцию 
на вектор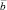 
обозначают так:
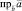(или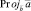 
).
Запись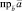 
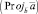читают: проекция вектора а на вектор бэ.
Запись пр – это сокращение от слова «проекция».
Запись Рroj – это сокращение от слова projection (проецирование).
Проекцию 
на вектор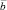 
(рисунок) находят по формуле
где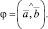 
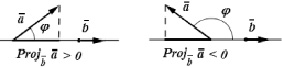
Проекция 
на вектор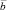 
Если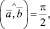 
то векторы 
и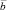 
перпендикулярны друг другу.
Записывают: 
.
Перпендикуляр (лат. perpendicularis – отвесный) к прямой – прямая линия (отрезок), которая пересекает данную прямую и образует с ней угол 90 градусов (под прямым углом.
Опустить перпендикуляр – значит провести через точку прямую, перпендикулярную другой прямой.
Если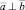 
, то проекция 
на вектор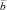 
есть точка.
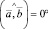Если 
или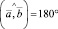 
, то векторы 
и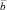 
– параллельные векторы.
Записывают: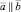 
.
Затем студентам предлагается либо составить самостоятельно вопросы и задать их друг другу, либо ответить на вопросы, которые задает им преподаватель.
Например, ответьте на вопросы и выполните задания:
1. Что такое проекция вектора 
на вектор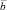 
?
2. Как обозначают проекцию 
на вектор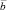 
?
3. Как читают запись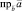 
?
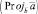4. Напишите формулу, по которой находят проекцию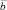 
на вектор 
.
5. Когда векторы 
и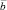 
перпендикулярны друг другу? Запишите символами: вектор 
перпендикулярен вектору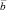 
.
6. Что такое перпендикуляр?
7. Что значит опустить перпендикуляр?
8. Когда вектор 
параллелен вектору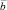 
? Запишите символами: вектор 
параллелен вектору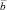 
?
Такое задание направлено на закрепление иностранными слушателями темы «Проекция вектора». Студенты при изучении данной темы должны научиться читать проекцию вектора на вектор, знаки перпендикулярности и параллельности векторов.
Работа с заданием помогает иностранным слушателям повторить тему «Проекция вектора». Студенты при изучении данной темы должны научиться читать проекцию вектора на вектор.
3. Задание – микросочинение.
Сначала студент должен прочитать утверждение, понять его смысл на русском языке, проанализировать, верно или нет утверждение, и только потом сформулировать обоснованный ответ.
Приведем примеры заданий.
Задание. Правильно ли утверждение? Обоснуйте ответ.
Утверждение: если сумма двух слагаемых – чётное число и эти слагаемые – натуральные числа, то каждое слагаемое – чётное число.
Для того чтобы обучающийся дал ответ на поставленный вопрос, ему необходимо вспомнить, что такое сумма, слагаемое, четное число, натуральное число, затем понять смысл утверждения на русском языке и только потом дать ответ и обосновать его.
Задание.
4. Задание – модель.
Задания четвертого типа преподавателю математики помогает создать преподаватель русского языка как иностранного.
Рассмотрим примеры.
Задание. Прочитайте конструкции и примеры их использования, определите падеж существительных. Поставьте существительные в скобках в правильную форму [2].
Модель: Что? называется чем?
Уравнение вида
ax2 + bx + c = 0,
где a, b, c – некоторые числа, a 0, x – неизвестное, называется квадратным _________________ (уравнение).
Модель: Что? обозначается чем/как?
Множества обозначают большими латинскими буквами: А, В, С и т.д.
Элементы множества записывают в фигурных ______________________ (скобки).
Работа с заданиями четвертого типа (задание – модель) предоставляет возможность иностранным слушателям изучить конструкции формулировок определений, утверждений в математике, теорем и т.д. Формирование умений у иностранных слушателей составлять математические определения – одна из задач преподавателей математики.
5. Задание – освоение математической символики.
Приведем примеры заданий пятого типа.
Задание. Прочитайте запись:
a > b ? a – b > 0.
Чтобы прочитать запись, студент должен занть, как читать символ ? и знаки «–», «>».
Задание. Прочитайте определение:
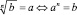(a ≥ 0, b ≥ 0).
Данное задание требует от студента умения читать символ ?, знак сравнения ≥, степень an и алгебраический корень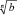 
.
Задание. Запишите, используя символы, свойство степени: Чтобы разделить степени с одинаковыми основаниями, нужно основание оставить без изменения (основание не изменять), а показатели вычесть (из показателя делимого вычесть показатель делителя).
Выполняя такое задание, иностранному студенту сначала надо понять, о чем идет речь в задании, вспомнить, что такое степень и какое свойство записано в задании, и только потом записать его через символы.
Задания пятого типа способствуют развитию словесно-символического способа изложения информации и создают условия для развития речевого мышления слушателей подготовительного отделения.
Заметим, что иностранные слушатели не владеют русским языком, и обучение математике начинается с разделов математики начальной школы. И менее чем за год иностранные слушатели повторяют практически все разделы школьной математики на русском языке, которые российские школьники изучают на протяжении 11 лет.
В конце учебного года нами было проведено анкетирование, целью которого было выяснение формы организации учебного процесса, которая эффективнее способствует формированию языковой компетенции по предмету. В анкетировании приняли участие 85 иностранных слушателей подготовительного отделения ТПУ, обучающихся в 2015–2016 уч. г.
Студенты, у которых занятия проходили в аудитории с круглым столом, отметили следующие преимущества. Во-первых, в силу малочисленности групп иностранных слушателей (8–12 человек) общение преподавателя с обучающимися и обучающихся друг с другом происходит на одном уровне глаз – друг напротив друга [1]. Во-вторых, в такой аудитории удобно вести диалог, подводить итоги занятий, обсуждать план выполнения домашнего задания. Все это способствовало развитию устной речи обучающихся на неродном языке.
В аудиториях, где столы расставлены в один ряд, студенты отметили, что они видели только глаза преподавателя, и поэтому работать им друг с другом было неудобно, особенно если они сидели не рядом.
Большая часть иностранных слушателей (98 % из опрошенных) отметили, что на начальном этапе им помогла работа в статичных группах (группах постоянного состава).
Часть респондентов (83 % из опрошенных) отметила, что для них контроль, осуществляемый преподавателем, был более плодотворен, потому что преподаватель объяснял, какие они сделали ошибки, как правильно построить ответ или написать его. Большинство студентов (94 % из опрошенных) отметили, что им было важно, чтобы преподаватель не только объяснял им ошибки, но и исправлял ошибки в словах красной пастой, объяснял им, почему так надо писать и где поставить ударения в словах.
После двух месяцев обучения мы вводили в процесс обучения работу в мигрирующих группах (находящихся в движении). Около 30 % иностранных слушателей отметили, что им было тяжело работать в парах с иностранными слушателями, т.к. они плохо понимали сначала их речь. Это объясняется тем, во-первых, что студенты плохо владеют русским языком на этом этапе, во-вторых, студенты из Китая и Вьетнама имеют особенности, которые им не позволяют правильно произносить многие буквы русского алфавита, такие как, например, «р» и «л».
Также заметим, что в смешанных группах формирование языковой компетенции по предмету проходило успешнее, потому что язык общения в группе был русский. Если же основную часть группы составляли студенты из одной страны (например, из Китая), то студенты часто (во время перерыва или после занятий) переходили на родной язык, что затрудняло их обучение на русском языке.
Небольшая часть иностранных слушателей (9 % из опрошенных) отметили, что они быстро освоили русский язык, потому что в общежитии они жили с русскоговорящими студентами и их общение проходило на русском языке и вне стен вуза.
Ограниченное время обучения иностранных слушателей подготовительного отделения (не более десяти месяцев) побуждает преподавателей постоянно совершенствовать методику преподавания на неродном языке. В современных условиях преподавателю необходимо не только изыскивать новые пути повышения эффективности аудиторной работы, но и совершенствовать уже имеющиеся, дополняя их новыми возможностями.
Опыт преподавания показал, что работа с заданиями рассмотренных типов позволяет преподавателю проверить усвоение иностранными слушателями математических терминов и понятий и способствует формированию владения формами устной речи и математической лексикой на русском языке.
В заключение отметим, что организация процесса обучения иностранных студентов в техническом вузе позволяет применять разные формы проведения занятий, что дает возможность направить процесс обучения в новое русло и повысить у студентов интерес к изучению предмета.