В настоящее время в частотной парадигме релевантности по эффективности обработки информации фактически достигнут предел, однако рост объемов информации и возрастающие требования к качеству ее обработки усиливают внимание к использованию семантических подходов. Данное обстоятельство особенно явно проявляется в областях информационного поиска и классификации документов. В то же время использованию семантических подходов препятствует отсутствие приемлемой формализации, что обусловлено сложностью и неоднозначностью естественных языков (ЕЯ), порождающих многочисленные исследования в данном направлении, например [3, 4]. Предлагаемая работа отражает часть наших исследований по семантической интерпретации текстов научно-технического стиля, обобщая и развивая, в частности, результаты работ [1, 2, 5].
Метод
Суть предлагаемого подхода состоит в формировании смысла текстового фрагмента (ТФ) с помощью вычислительной процедуры над смысловыми значениями его слов. Процедура конструируется в виде семантической схемы (СемСх), которая положена в основу сравнения ТФ на смысловую близость, а для сравнения специально сконструирован семантический критерий близости (СКБ).
A. Основные термины и понятия
Пусть в ЕЯ задана некоторая цепочка q слов ai вида
q = a1a2...an, (1)
представляющая целостный по смыслу ТФ. Целостность означает, что между словами цепочки q существует отношение непосредственного подчинения, оно задается словосочетаниями и является однозначным.
Если в некотором словосочетании a – главное слово, а b – зависимое, то эту зависимость представим выражением (записью) вида
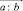, (2)
в котором стрелка указывает на направление зависимости слов.
Если а – некоторое слово, входящее главным словом в несколько словосочетаний с зависимыми словами b1, b2, ..., bp, тогда зависимость запишем выражением вида
a: {b1, b2, ..., bp}, (3)
которое назовем его контекстной связкой.
Обозначим через S(ai) множество смысловых значений слова ai из q (1), а множество смысловых значений ФТ (1) представим функционалом вида
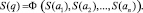(4)
Если в ТФ q слово ai является главным, то для (4) справедливо соотношение
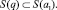(5)
Таким образом, смысловое значение словосочетания есть подмножество смысловых значений его главного слова, задается оно смыслом зависимого слова, образующего контекст:
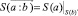(6)
Для (6) справедливы соотношения
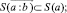
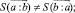
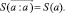(7)
На словосочетании следующим образом определим операцию контекстного уточнения смысла главного слова зависимым:
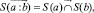(8)
где 
– операция контекстного уточнения смысла, а стрелка над ней задает направление зависимости слов в словосочетании. Распространяя (8) на контекстную связку (3), получим
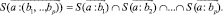(9)
Теперь с учетом (8) и (9) для ТФ можно уже строить множество смысловых значений (4).
Поясним рассуждения примером ТФ q, где слова закодированы латинскими буквами:
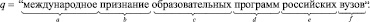
Используя (8) и (9) для примера ТФ q, получим выражение его смыслового значения:
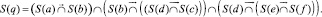(10)
B. Обратная польская запись функционала текстового фрагмента, семантическая схема
Основную особенность обратной польской записи (ОПЗ) представляет способ ее вычисления, он же однозначно определяет структуру вычислительной процедуры. Используем данное обстоятельство и распространим нотацию ОПЗ на функционал смысла.
В нотации ОПЗ операция контекстного уточнения смысла (8) будет иметь вид
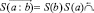(11)
В (11) для сохранения зависимости слов стрелка над операцией меняет направление.
Также ОПЗ контекстной связки (9) с учетом (11) принимает следующий вид:
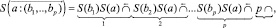(12)
где p соответствует арности операции пересечения.
Применяя (11) и (12) к ТФ q (10), получим следующую ОПЗ:
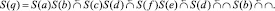(13)
Промежуточные выражения пошагового вычисления ОПЗ (13) имеют вид
1. 
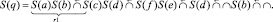
2. 
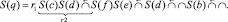
3. 
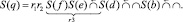
4. 
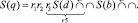
5. 
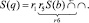
6. 
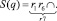
7. 
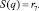
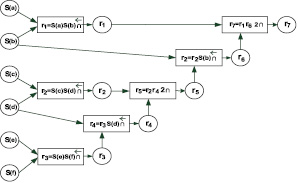
Рис. 1. Семантическая схема ТФ q
Здесь переменные ri являются временными и предназначены для хранения промежуточных результатов каждого шага. Пока важен только факт их существования.
Поставим в соответствие каждой операции графический элемент, в котором прямоугольник представляет операцию, круглые вершины слева – входные данные, справа – результат. Такое представление назовем элементом смысла. Объединяя элементы смысла выражения (13), получим графическое представление всей вычислительной процедуры, которое назовем семантической схемой (СемСх). Вычислительная схема, построенная для примера ТФ в виде ОПЗ (13), представлена ниже на рис. 1 и имеет следующий вид:
C. Критерий сравнения текстовых фрагментов на семантическую близость
Пусть задан ТФ q в виде (1), который назовем образцом сравнения. Данный образец сравним на семантическую близость с ТФ t вида
t = b1b2...bm, (14)
для чего введем критерий семантической близости (КСБ) следующим образом:
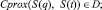D = [0...1]. (15)
Здесь Сprox – КСБ, S(q) – множество смысловых значений образца, S(t) – множество смысловых значений ТФ t, а D – интервал значений КСБ Сprox. Если Сprox = 0, то близость между q и t отсутствует, при Сprox = 1 имеет место полное семантическое совпадение.
Отметим, что в общем случае всегда справедливо соотношение
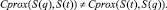(16)
Представим КСБ в виде доли совпадающих элементов смысла в СемСх образца q и сравниваемого ТФ t к общему числу элементов смысла образца:
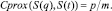(17)
Здесь m – число элементов смысла в СемСх образца q, p – число совпадающих элементов смысла q в СемСх t соответственно. Частным случаем (17) является частотный критерий релевантности (φ), когда m представляет число слов в ТФ q, а p – число слов из q, совпадающих со словами в t.
Поясним семантическое сравнение образца q и на примерах конкретных ТФ. Одновременно для примеров сравним КСБ и частотный критерий релевантности.
Пример 1. Пусть задан первый ТФ_1 в виде предложения:
Правительство России проводит политику, направленную на международное признание образовательных программ российских вузов.
Здесь образец q является подстрокой ТФ_1 (выделено курсивом) и его СемСх полностью укладывается в СемСх ТФ_1. Соответственно Cprox(S(q), S(t)) = 1 и φ = 1.
Пример 2. Пусть задан второй ТФ_2 вида
Образовательные программы российских вузов нуждаются в международном признании».
В ТФ_2 подчеркнутым курсивом выделены подстроки, совпадающие с фрагментами образца.
Выделим совпадающие элементы смысла на СемСх образца жирными линиями, тогда СемСх образца примет вид, показанный на рис. 2.
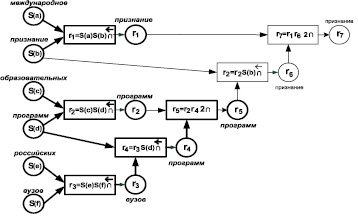
Рис. 2. Результат сравнения на близость образца q и ТФ_2
СемСх образца содержит 5 совпадающих элементов смысла, поэтому Cprox(S(q), S(t)) = 5/7 и его значение еще достаточно велико. В то же время критерий близости φ = 1, он изменения смысла не чувствует, поскольку все слова образца входят в ТФ_2.
Пример 3. Пусть задан третий ТФ_3 вида
Международное признание образовательных программ поднимает репутационный рейтинг российских вузов».
После сравнения СемСх образца представлена на рис. 3. Здесь нетрудно заметить, что СемСх образца и ТФ_3 имеют всего три совпадающих элемента смысла, поэтому Cprox(S(q), S(t)) = 3/7. Действительно, смысловая близость образца и ТФ_3 имеет именно эту оценку. Однако φ = 1 и он снова не чувствует изменение смысла.
Пример 4. Пусть задан четвертый ТФ_4 вида
Международное признание вузов увеличивает возможности России по привлечению иностранных студентов.
Результат сравнения образца q и ТФ_4 показан на рис. 4.
Из рис. 4 видно, что СемСх образца имеет один совпадающий элемент смысла и Cprox(S(q), S(t)) = 1/7 достаточно мал. В то же время значение φ = 0,5 еще высоко, поскольку половина слов образца входит во фрагмент текста.
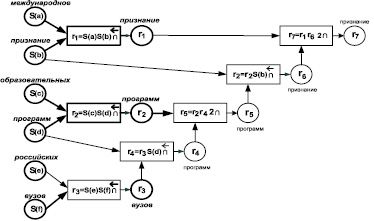
Рис. 3. Результат сравнения на близость образца q и ТФ_3
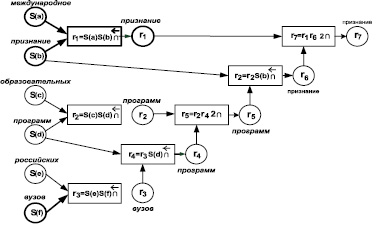
Рис. 4. Результат сравнения на близость образца ТФ_4
Пример 5. Рассмотрим пятый ТФ_5:
Международные программы академических обменов и участие в них российских ученых способствуют улучшению образовательного процесса вузов России.
Результат сравнения на близость СемСх образца и Сем Сх ТФ-5 показан ниже на рис. 5.
СемСх образца не имеет совпадающих элементов смысла с СемСх ТФ_5, поэтому Cprox(S(q), S(t)) = 0. В то же время φ = 0,83, поскольку 5 слов образца из 6 входит в ТФ_5.
Из приведенных примеров видно, что СКБ реально отражает семантическую близость образца и ТФ, в то время как значение частотного критерия не всегда отражает реальную семантическую близость. Особенно это явно проявляется в пятом примере.
D. Семантический информационный поиск и классификация документов.
Семантическую близость документов образцу (поисковому запросу) определим лингвистической переменной SemProx вида
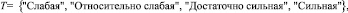(18)
где каждый терм терм-множества T является нечеткой переменной подынтервалов [0...p1), [p1...p2), [p2...p3), [p3...1] шкалы D соответственно.
Построим процедуру определения семантической близости документа запросу следующим образом. Для каждого предложения документа определим значение Cprox. Далее для каждого подынтервала шкалы D подсчитаем число попавших в него значений Cprox, после чего построим из этих чисел характеристический вектор документа вида
<(fслабая),(fотносительно слабая),(fдостаточно сильная),(fcильная)>
Вычисление лингвистической переменной реализуем процедурой Semantic_proximity (Dос, SemProx), в которой Dос – анализируемый документ, SemProx – возвращаемое значение лингвистической близости. Вычисление проведем по решающим правилам вида
IF ((fслабая>(fдостаточная +fсильная))&(fслабая>fотносительная) THEN SemProx?“Слабая“:;
IF ((fотносительная>(fдостаточная + fсильная))& (fотносительная>fслабая) THEN SemProx:“Относительно слабая“;
IF ((fдостаточная>(fслабая + fотносительная))& (fдостаточная>fсильная) THEN SemProx:“Достаточно сильная“;
IF ((fсильная>(fслабая + fотносительная))& (fсильная>fдостаточная) THEN SemProx :“Сильная“.
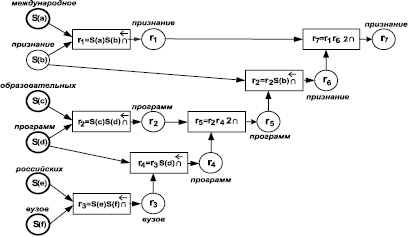
Рис. 5. Результат сравнения на близость образца q и ТФ_5
Само включение документа в ВЫДАЧУ R реализуем простым способом:
BEGIN
WHILE (конец потока документов)
DO BEGIN
Semantic_proximity (Dос, SemProx);
IF (Semprox=(условие включения)) then D>R;
END
END.
Здесь > включение документа D в ВЫДАЧУ R. Введение условий для разных R превращает процедуру в семантический документный классификатор.
Заключение
Вычислительная модель семантической интерпретации на основе семантических схем позволяет перейти к формально математическому сравнению текстов на семантическую близость и организовать на этой основе высокоточный информационный поиск и классификацию документов. Особенно это актуально при семантическом различении текстов, использующих одну и ту же терминологию.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-07-00241\16.