В связи с растущим количеством информации, представленной в виде графовых структур, их анализ становится центральной проблемой компьютерных наук в области анализа данных. Для некоторых задач величины графов превзошли возможности современных алгоритмов. Подобная тенденция ведет к нескольким интересным задачам, одной из которых является масштабирование алгоритмов с размером графа, если оригинальный алгоритм очень медленный.
В данной статье мы концентрируемся на решении проблемы сопоставления пользователей и их связей, представленных в графовых структурах разных социальных сетей больших размеров, принимая во внимание только топологии графовых структур, в связи с тем, что один из подаваемых графов полностью анонимизирован. Под большими графами мы понимаем графы с количеством вершин более двух миллионов и средним ветвлением больше 30. К дополнительным ограничениям относится тот факт, что доля пользователей представленных уникальными вершинами в двух графах могут иметь разный набор ребер и более того, пользователь может отсутствовать во второй сети, таким образом задачу сопоставления графов уже нельзя будет свести к задаче изоморфизма двух графов в связи с тем, что целевая функция сопоставления 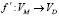 не является биективной. Данную задачу можно определить как неполное сопоставление графов (далее НСГ), стойкую к некоторому малому набору ошибочных сопоставлений: даны два графа
не является биективной. Данную задачу можно определить как неполное сопоставление графов (далее НСГ), стойкую к некоторому малому набору ошибочных сопоставлений: даны два графа 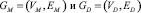 ,
, 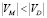 , задача заключается в том чтобы найти инъективную функцию
, задача заключается в том чтобы найти инъективную функцию 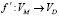 , такую что
, такую что 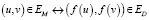 . Соответствующая задача разрешимости приведённой к задаче изоморфизма GM и подграфа GD является NP-полной, вследствие того, что это частный случай поиска максимального общего подграфа и поэтому не имеет полиномиального решения, даже если алгоритм ограничен по области применения (в предположении P ≠ NP). Применение НСГ над огромными графами можно найти в таких задачах, как деанонимизация графа социальных сетей [6], чем на данный момент занимаются большие ИТ-компании для улучшения своей социальной сети за счет деанонимизации других социальных сетей, еще одно применение можно найти в сопоставлении сети взаимодействия протеинов разных видов животных для выявления общих частей, отвечающих за схожее функционирование в живом организме [3]. Метод решения проблемы НСГ, учитывающий только топологию графов, является по своей сути основой для будущих алгоритмов сопоставления графов в связи с ее обобщенностью над структурой графов.
. Соответствующая задача разрешимости приведённой к задаче изоморфизма GM и подграфа GD является NP-полной, вследствие того, что это частный случай поиска максимального общего подграфа и поэтому не имеет полиномиального решения, даже если алгоритм ограничен по области применения (в предположении P ≠ NP). Применение НСГ над огромными графами можно найти в таких задачах, как деанонимизация графа социальных сетей [6], чем на данный момент занимаются большие ИТ-компании для улучшения своей социальной сети за счет деанонимизации других социальных сетей, еще одно применение можно найти в сопоставлении сети взаимодействия протеинов разных видов животных для выявления общих частей, отвечающих за схожее функционирование в живом организме [3]. Метод решения проблемы НСГ, учитывающий только топологию графов, является по своей сути основой для будущих алгоритмов сопоставления графов в связи с ее обобщенностью над структурой графов.
Подходы и обоснование
Поиск структурного сопоставления в теории графов, известного как решение проблемы изоморфизма, имеет более общую задачу – сопоставление графов допускающая неточности (НСГ). Ниже приводим список самых известных подходов на данный момент для решения проблемы сопоставления небольших графов [2].
1. Редактирование дистанции: этот подход основан на интуитивно понятном измерении расхожести на графах при помощи поддерживаемого «расстояния редактирования». Этот подход имеет решения для точного системного сопоставления структуры и для подхода устойчивого к ошибкам с верхней границей точного расстояния редактирования. Целью является трансформация одного графа к другому путем некоторого числа операций (добавление, удаление, замещение вершин или ребер и перестановка ребер). Каждая операция ассоциируется со стоимостью, таким образом данный метод стремится найти последовательность операций минимизирующие оценку сопоставления графов. Несмотря на то, что подобный подход хорошо подходит для НСГ, его вычислительная сложность экспоненциально зависит от числа узлов в графах. Таким образом, для решения нашей проблемы подобный метод считается неприменимым.
2. Редактирование дистанции учитывающее вероятность: идея заключается в моделировании распределения операции редактирования в пространстве имен вершин. Так как мы решаем задачу сопоставления анонимизированных графов, то данный способ тоже не применим вследствие наличия анонимизированного графа.
3. Вычисление максимального подграфа: основано на решении проблемы поиска максимальной клики в ассоциированном графе. Этот подход имеет решения для точного системного сопоставления структуры и для подхода допускающий мелкие погрешности, однако проблема поиска максимальной клики в свою очередь является NP-полной.
Самые масштабируемые методы СГ используют идеи из теории перколяции. Этот класс алгоритмов требует начальный набор изначально правильно сопоставленных вершин (далее семена), которые впоследствии используются как катализатор процесса одновременной перколяции над двумя графами. При процессе перколяции происходит массовая генерация пространства решений как пар кандидатов и далее применяются функции выбора соответствующих пар за счет контекстных данных каждой пары. Таким образом, подобные алгоритмы отличаются большой скоростью и динамическим сопоставлением, что можно будет использовать впоследствии над динамическими графами. Для деанонимизации сети были выбраны два самых эффективных алгоритма – НСГ на основе теории перколяции ExpandWhenStuck [5], который в свою очередь является расширением PercolationGM (PGM) [7]. Далее был проанализирован метод решения НСГ, основанный на теории перколяции, и были выявлены слабые стороны данного метода. Мы предлагаем способы их решения и обоснование возникающих ошибок, что будет полезным для дизайна улучшенного алгоритма НСГ графов на основе теории перколяции.
Постановка задачи
На вход подаются два простых неориентированных графа 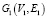 – анонимизированный и
– анонимизированный и 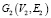 вершины V1,2 которые представляют одну и ту же сущность из множества сущностей H
вершины V1,2 которые представляют одну и ту же сущность из множества сущностей H 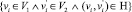 . Далее, мы убираем метки с вершин и ребер G2. Так же на вход подается множество изначально сопоставленных пар
. Далее, мы убираем метки с вершин и ребер G2. Так же на вход подается множество изначально сопоставленных пар 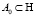 (далее семена), определенного размера
(далее семена), определенного размера 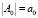 . Процесс сопоставления использует только структуру графов, которая представлена множеством вершин V и ребер E.
. Процесс сопоставления использует только структуру графов, которая представлена множеством вершин V и ребер E.
Оценка результатов НСГ проводится следующим образом:
1. 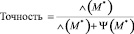 ,
,
где 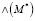 – количество правильных сопоставлений и
– количество правильных сопоставлений и 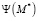 – количество неправильных сопоставлений.
– количество неправильных сопоставлений.
2. 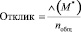 ,
,
где nобщ – число пересечений вершин в обоих графах.
3. F1–оценка = 2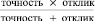 .
.
F1–оценка∈[0, 1] представляет из себя комбинацию оценок Точности и Отклика. Если F1–оценка > 1 тогда Точность > 1, что говорит о том, что доля ошибок в М* очень мала, таким же образом Отклик > 1 говорит о том, что большая часть вершин присутствующих в G1,2 сопоставлены правильно. Наша основная задача – максимизировать целевую функцию – F1–оценка.
Модель случайного дуплицирования графа для тестирования алгоритма
Удобный подход для оценки алгоритмов СГ – это проверка его эффективности над моделью 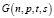 , которая позволяет генерировать два графа с пересечениями [5]. Биграфовая модель
, которая позволяет генерировать два графа с пересечениями [5]. Биграфовая модель 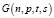 генерирует два графа
генерирует два графа 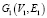 и
и 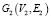 следующим образом:
следующим образом:
1. Генерируется граф 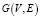 по заранее выбранной модели случайного графа [1]: Эрдеша – Реньи, Барабаши – Альберта либо Чунг-Лу.
по заранее выбранной модели случайного графа [1]: Эрдеша – Реньи, Барабаши – Альберта либо Чунг-Лу.
2. Множество вершин V1,2 выбирается случайным образом из множества V с вероятностью t.
3. Множество ребер E1,2 выбирается случайным образом из множества E с вероятностью s. Результат F1–оценка мы получаем из G1,2 путем верифицирования результирующих сопоставлений М* через 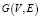 .
.
Метод деанонимизации графов на основе перколяции
Граф G представлен как V – набор вершин и E – набор ребер. Дается два графа: 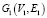 и
и 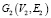 . Степень ветвления вершин i и j в графах G1 и G2 обозначается как d1,i и d2,j. Ребро в графе представлено как
. Степень ветвления вершин i и j в графах G1 и G2 обозначается как d1,i и d2,j. Ребро в графе представлено как 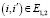 . Пара вершин представляется как
. Пара вершин представляется как 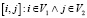 . Каждая пара [i, j] имеет соседа
. Каждая пара [i, j] имеет соседа 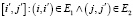 . Пара
. Пара 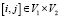 соответствует какой-то единственной сущности (к примеру, человек), с чем алгоритм и работает. Нужно найти соответствующие пары вершин
соответствует какой-то единственной сущности (к примеру, человек), с чем алгоритм и работает. Нужно найти соответствующие пары вершин 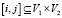 , основываясь только на топологии двух сетей (непомеченные вершины и ребра), притом V1,2 и E1,2 могут не пересекаться полностью.
, основываясь только на топологии двух сетей (непомеченные вершины и ребра), притом V1,2 и E1,2 могут не пересекаться полностью.
Изначально у нас имеются активированные пары A0 в размере 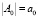 и граничный уровень r ≥ 2, что является минимально возможной границей перколяции. В процессе сопоставления вершин графов, другими словами, выбора пары из множества кандидатов S, пополняется множество результатов M (сопоставленных пар), начальное значение которого
и граничный уровень r ≥ 2, что является минимально возможной границей перколяции. В процессе сопоставления вершин графов, другими словами, выбора пары из множества кандидатов S, пополняется множество результатов M (сопоставленных пар), начальное значение которого 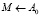 . Так как мы ищем инъективную функцию
. Так как мы ищем инъективную функцию 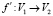 в предположении, что
в предположении, что 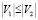 , то
, то 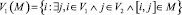 и V2(M) не могут иметь повторяющиеся вершины.
и V2(M) не могут иметь повторяющиеся вершины.
Процесс перколяции над графами – это процесс активации вершин в графе, в нашем случае мы проводим перколяцию над двумя графами одновременно, таким образом – это процесс активации пары вершин [i, j]. A(τ) – активированные и Z(τ) – использованные пары во время τ, изначально 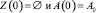 . На каждом временном шаге τ одна выбранная пара (далее активированная пара)
. На каждом временном шаге τ одна выбранная пара (далее активированная пара)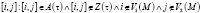
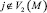 распространяет баллы по соседним парам, раздавая по одному баллу каждому из [i’, j’] и далее переходит во множество результатирующих сопоставлений М и после этого переходит во множество использованных пар Z. Пара из множества кандидатов S активируется во время τ, если по крайней мере r число соседних пар были активированы и использованы ранее. Оценка пары из множества кандидатов A определяется количеством полученных баллов в процессе перколяции графа, то есть в процессе раздачи баллов активизированными парами. В большинстве случаев среди пар в A встречается несколько пар с максимальной оценкой, таким образом, для максимизации вероятности правильного сопоставления пары мы выбираем [i, j] такую, что разность ветвлений вершин представленных в паре имеет наименьшее значение:
распространяет баллы по соседним парам, раздавая по одному баллу каждому из [i’, j’] и далее переходит во множество результатирующих сопоставлений М и после этого переходит во множество использованных пар Z. Пара из множества кандидатов S активируется во время τ, если по крайней мере r число соседних пар были активированы и использованы ранее. Оценка пары из множества кандидатов A определяется количеством полученных баллов в процессе перколяции графа, то есть в процессе раздачи баллов активизированными парами. В большинстве случаев среди пар в A встречается несколько пар с максимальной оценкой, таким образом, для максимизации вероятности правильного сопоставления пары мы выбираем [i, j] такую, что разность ветвлений вершин представленных в паре имеет наименьшее значение: 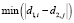 , в этом случае вероятностью того, что i = j больше чем i ≠ j [5]. Результатом является множество сопоставленных пар М*, которое мы получаем при затухании процесса перколяции (остановка алгоритма), число правильно сопоставленных пар обозначается
, в этом случае вероятностью того, что i = j больше чем i ≠ j [5]. Результатом является множество сопоставленных пар М*, которое мы получаем при затухании процесса перколяции (остановка алгоритма), число правильно сопоставленных пар обозначается 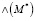 , неправильных
, неправильных 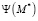 .
.
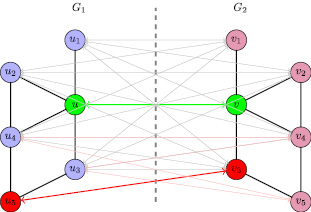
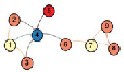
Рис. 1. Вершины u1, u2, u3 и u4 не сопоставленные соседи вершины u. Вершины u4 и u3 не сопоставленные соседи неправильно сопоставленной вершины u5. После генерации новых кандидатов из соседних пар сопоставленной пары [u, v] и разброса баллов по всем соседним парам мы получаем [u4, v4] и [u4, v3] кандидатов на сопоставление, как результат, будет выбрана пара [u4, v4] имея большую оценку и 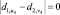
Параметр 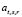 определяет число начальных семян для пересечения уровня фазового перехода в модели случайного графа Эрдеши – Реньи, примененной к дуплицированию графа, описанном выше. Для того, чтобы в результате иметь только корректные сопоставления над идентичными графами
определяет число начальных семян для пересечения уровня фазового перехода в модели случайного графа Эрдеши – Реньи, примененной к дуплицированию графа, описанном выше. Для того, чтобы в результате иметь только корректные сопоставления над идентичными графами 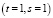 , достаточно иметь границу перколяции r = 4 и, как минимум
, достаточно иметь границу перколяции r = 4 и, как минимум 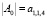 [4], что удалось доказать только для случайного графа Эрдеша – Реньи.
[4], что удалось доказать только для случайного графа Эрдеша – Реньи.
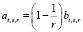 (минимальный размер семян на вход алгоритму),
(минимальный размер семян на вход алгоритму),
где 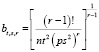 .
.
Для 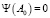 нужно
нужно 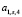 (r = 4) семян.
(r = 4) семян.
Теорема об устойчивости к шумным активизированным парам [5] гарантирует, что множество семян размера 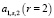 достаточно для сопоставления всех вершин с низким
достаточно для сопоставления всех вершин с низким 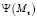 что требует значительно меньше начальных сопоставлений для начала перколяции
что требует значительно меньше начальных сопоставлений для начала перколяции 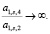 Доказательство структурировано на поиске нижней и высшей границы доли ошибок, генерируемых за процесс перколяции [5].
Доказательство структурировано на поиске нижней и высшей границы доли ошибок, генерируемых за процесс перколяции [5].
Проведение экспериментов
Данные для эксперимента были получены путем генерации случайных графов Барабаши – Альберта, Чунг – Лу [1] и одного реального графа социальной сети Facebook небольшого размера. Дуплицирование графов для оценки алгоритмов проводится с параметрами t = 1 и s = 1. Для экспериментальных целей было выбрано 2 алгоритма, основанных на прочной идее, описанной в статье «Bootstrap percolation on the random graph G(n, p)» [4]. Результаты представленны в таблице.
1. Percolation Graph Matching (PGM) [7] с пониженной фазовой границей r = 2. Данный алгоритм по большей части зависит от начальных сопоставлений A0 в связи с тем, что в процессе перколяции не происходит генерации семян.
2. ExpandWhenStuck [5] имеет пониженную планку к A0, за счет самогенерации семян и стабильности к неправильным сопоставлениям. Всякий раз, когда у алгоритма не имеется кандидатов со счетом в 2 балла и выше, он не прекращает перколяцию как PGM, в свою очередь, он продолжает перколяцию за счет расширения множества семян парами из множества неиспользованных Z и не входящих во множество результатов M, полученных от смежных уже сопоставленных вершин M: A < соседние пары [i, j] от каждой пары из
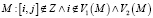 .
.
Слабые стороны алгоритмов перколяции и общие подходы для их решения
НСГ на основе перколяции неспособно сопоставить вершины с единичной степенью ветвления вследствие того, что границы фазового перехода r = 2. Стало очевидным, что граф, имеющий некоторое множество листьев, никогда не получит полный Отклик (рис. 2, а, вершина 5). Более того, это влечет к невозможности сопоставить вершину-мост в случае, если этот мост – единственное соединение двух кластеров и перколяция происходит только в одном кластере, как результат, второй кластер не приступит к перколяции, что повлечет к очень низкому Отклику (рис. 2, а, вершина 6). Стоит отметить, что несопоставленные листья будут находиться во множестве кандидатов S, причем каждая из этих пар с высокой вероятностью является правильным сопоставлением, таким образом, возможно при полной остановке перколяции пополнить

и заново запустить алгоритм перколяции. Таким образом, листья будут сопоставлены и тем же образом перколяция пройдет через пару-мост к кластеру, где и продолжится перколяция.
Как было выявлено в теореме об устойчивости к ошибочным семенам, алгоритм СГ может продолжать процесс перколяции даже с ошибочными семенами и прийти к хорошим результатам. Все же, стоит уделить внимание снижению влияния неправильных сопоставлений до самого минимума. Процесс перколяции может сталкиваться с таким случаем, как состояние неподкрепленности принятия решения, которое основано лишь на оценках пары и разности ветвлений ее вершин. Во множестве кандидатов А при выборе пар с максимальной оценкой далее проверяется ветвление вершин в паре на минимальную разность, и вполне возможен случай, когда таких пар несколько. В итоге это ведет к случайному неподкрепленному выбору пары из A во множество сопоставлений M.
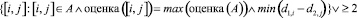 .
.
Пример приведен на рис. 2, б
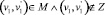
и
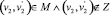 ,
,
после распространения баллов по соседним парам 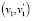 и
и 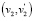 мы пополняем множество кандидатов
мы пополняем множество кандидатов 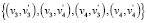 , пары данного множества получают одинаковое количество баллов, притом вершины каждой из этих пар имеют одинаковую степень ветвления = 5. Таким образом, существующий алгоритм просто не в силах сделать взвешенный выбор для кандидата на сопоставление во множество M, что скажется на снижении оценки Точности. Как решение, в таких случаях можно создавать «обобщающую вершину» на каждом из двух графов, которая будет представлена как вершина кодирующая в себе несколько вершин, и далее пара из данных обобщающих вершин
, пары данного множества получают одинаковое количество баллов, притом вершины каждой из этих пар имеют одинаковую степень ветвления = 5. Таким образом, существующий алгоритм просто не в силах сделать взвешенный выбор для кандидата на сопоставление во множество M, что скажется на снижении оценки Точности. Как решение, в таких случаях можно создавать «обобщающую вершину» на каждом из двух графов, которая будет представлена как вершина кодирующая в себе несколько вершин, и далее пара из данных обобщающих вершин 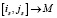 (рис. 2, в). Подобный подход еще интересен тем, что можно будет разработать в дальнейшем алгоритм архивации на основе перколяции.
(рис. 2, в). Подобный подход еще интересен тем, что можно будет разработать в дальнейшем алгоритм архивации на основе перколяции.
Выводы
Был проведен анализ алгоритмов НСГ на основе перколяции с генерацией семян для поддержки процесса перколяции. В процессе анализа перколяции для сопоставления графов, были выявлены слабые моменты:
1. Процессу перколяции по крайней мере требуется граница перехода r ≥ 2. В связи с этим листья не будут сопоставлены, что влечет плохой Отклик.
2. Невозможность сопоставить вершину-мост в случае, если этот мост – единственное соединение двух кластеров и перколяция происходит только в одном кластере, как результат, второй кластер не будет сопоставлен, что влечет более сильное ухудшение Отклика.
3. Состояние неподкрепленности принятия решения, встречаемое в процессе перколяции, влечет понижение оценки Точности.
|
а) листья и мосты остаются незамеченными |
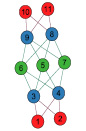
б) непредсказуемые пары для вершин начиная с 3 до 11 включительно |
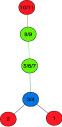
в) вершинное обобщение происходит в случаях нескольких кандидатов с одинаковыми параметрами (вершинное обобщение рис. 2, б) |
Рис. 2. Примеры случаев, с которыми не справляются современные алгоритмы НСГ на основе перколяции
Результаты представлены как (минимальное количество начальных семян / [F1-оценка * 100 %]) для двух синтетических графов и одного реального
|
случ. граф алгоритм |
Барабаши – Альберта |V| = 106 |
Чунг-Лу |V| = 2*105 |
Facebook |V| = 4039 |
|
PGM (r = 2) |
185 / 98,8 |
4 / 99,9 |
135 / 0,91 |
|
ExpandWhenStuck |
10 / 99,7 |
1 / 99,9 |
2 / 0,95 |
В данной работе были предложены причины и пути решения найденных проблем НСГ, основанного на теории перколяции. На основе проделанной работы мы усовершенствуем алгоритм НСГ и в дальнейшем планируем применить этот подход для реализации параллельной перколяции на платформе GPU для решения проблемы сопоставления графов.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-37-60089.