Двухэтапный процесс формирования транспортного расписания включает определение начального расписания и последующую его оптимизацию [1]. Под начальным расписанием понимается программно сформированное расписание при соблюдении обязательных ограничений, а его реализация представлена в [3]. Для оптимизации транспортных расписаний (NP-полной задачи) и, в частности, железнодорожных используются различные подходы, прежде всего в форме эвристик [5–9].
Целью статьи является представление эвристических методов оптимизации начального расписания движения пассажирского железнодорожного транспорта дальнего следования.
Задача оптимизации начального расписания решается последовательным выбором наиболее неравномерного маршрута и последующей его перестановкой в расписании в определяемое время отправления с начальной станции. Перестановка маршрута в расписании базируется на концепции равномерности. То есть выбираемое время перестановки, по крайней мере, не ухудшает показатели равномерности всего расписания. На каждом шаге решения задачи оптимизации начального расписания присутствуют две операции выбора и необходимость принятия некоторых решений. Такой подход характерен для жадных алгоритмов и применим для задач формирования расписаний и связанных с этим задач распределения ресурсов. Использование идеологии жадных алгоритмов требует цикличности процедур задачи формирования расписания. Операции выбора в представляемых алгоритмах являются многокритериальными и для их реализации привлечен аппарат методов ранжирования [2].
Введем необходимые в математическом моделировании расписания обозначения.
Исходные данные задачи:
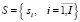 – множество станций железнодорожной сети;
– множество станций железнодорожной сети;
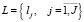 – множество перегонов железнодорожной сети;
– множество перегонов железнодорожной сети;
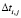 – минимальный интервал времени между двумя поездами при выезде/въезде с j-го перегона на i-ую станцию;
– минимальный интервал времени между двумя поездами при выезде/въезде с j-го перегона на i-ую станцию;
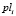 – количество платформ для высадки/посадки пассажиров i-ой станции;
– количество платформ для высадки/посадки пассажиров i-ой станции;
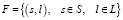 – множество инцидентных пар – станция s является одной из двух граничных станций перегона l. Количество элементов множества F составляет
– множество инцидентных пар – станция s является одной из двух граничных станций перегона l. Количество элементов множества F составляет 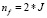 ;
;
nr – количество маршрутов железнодорожной сети;
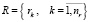 – множество векторов заявок маршрутов;
– множество векторов заявок маршрутов;
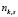 – количество станций маршрута rk;
– количество станций маршрута rk;
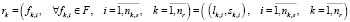 – (1)
– (1)
вектор заявок маршрута rk – последовательность пар перегон/станция от начальной станции до конечной;
nd – количество суток интервала расписания;
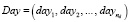 – упорядоченный во времени вектор суток;
– упорядоченный во времени вектор суток;
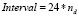 – интервал расписания, часы;
– интервал расписания, часы;
nk – количество суток отправления поездов k-ого маршрута;
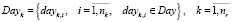 – множество суток отправления поездов маршрутов;
– множество суток отправления поездов маршрутов;
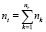 – количество поездов расписания;
– количество поездов расписания;
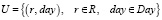 – множество инцидентных пар, частично формирующих заявки поездов маршрутов – поезд маршрута r отправляется с начальной станции в день day;
– множество инцидентных пар, частично формирующих заявки поездов маршрутов – поезд маршрута r отправляется с начальной станции в день day;
используя (1), получаем множество заявок поездов маршрутов:
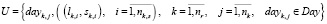 ; (2)
; (2)
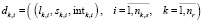 – заявка на прохождение маршрута k по i-ому перегону на i-ую станцию, где
– заявка на прохождение маршрута k по i-ому перегону на i-ую станцию, где 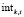 – интервал времени движения от i-1-ой до i-ой станции;
– интервал времени движения от i-1-ой до i-ой станции;
заявка на прохождение поезда 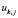 по i-ому перегону на i-ую станцию
по i-ому перегону на i-ую станцию
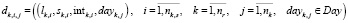 , (3)
, (3)
где 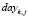 принимается равным дню отправления поезда маршрута.
принимается равным дню отправления поезда маршрута.
Исходные расчетные данные задачи:
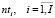 – количество поездов, проходящих через i-ую станцию;
– количество поездов, проходящих через i-ую станцию;
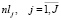 – количество поездов, проходящих через j-ой перегон.
– количество поездов, проходящих через j-ой перегон.
Переменные задачи:
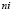 – количество оптимизированных (переставленных) маршрутов в расписании;
– количество оптимизированных (переставленных) маршрутов в расписании;
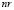 – количество не оптимизированных маршрутов в расписании;
– количество не оптимизированных маршрутов в расписании;
ti, tf – время прибытия/отправления поездов на станцию;
til, tfl – время выезда поездов на перегон и с перегона;
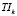 – время отправления поездов маршрута rk с начальной станции,
– время отправления поездов маршрута rk с начальной станции, 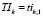 ;
;
событие расписания, порождаемое заявкой (3), по прохождению поезда 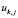 маршрута rk по i-ому перегону на i-ую станцию будет определяться следующим выражением:
маршрута rk по i-ому перегону на i-ую станцию будет определяться следующим выражением:
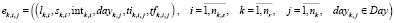 , (4)
, (4)
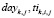 и
и 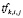 в (4) определяются на каждом шаге формирования расписания;
в (4) определяются на каждом шаге формирования расписания;
оценка равномерности распределения событий i-ой станции в интервале расписания
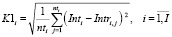 , (5)
, (5)
где 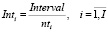 – среднее значение интервала между прибытиями поездов на i-ую станцию;
– среднее значение интервала между прибытиями поездов на i-ую станцию;
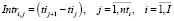 – величина интервала между прибытиями на станцию двух ближайших по времени поездов. Для
– величина интервала между прибытиями на станцию двух ближайших по времени поездов. Для 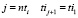 ;
;
оценка равномерности распределения событий i-ого перегона в интервале расписания
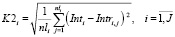 (6)
(6)
где 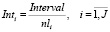 – среднее значение интервала между началами движения поездов по i-ому перегону;
– среднее значение интервала между началами движения поездов по i-ому перегону;
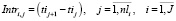 – величина интервала между началами движения поездов по i-ому перегону двух ближайших по времени поездов. Для
– величина интервала между началами движения поездов по i-ому перегону двух ближайших по времени поездов. Для 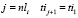 .
.
Задача оптимизации начального расписания состоит в цикличном выборе очередного маршрута 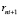 и формировании расписания
и формировании расписания 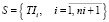 , которое минимизирует векторы оценок равномерности событий станций и перегонов
, которое минимизирует векторы оценок равномерности событий станций и перегонов
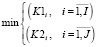 (7)
(7)
при обязательных ограничениях
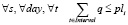 , (8)
, (8)
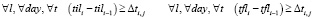 . (9)
. (9)
Целевая функция (7) обеспечивает многокритериальную минимизацию оценок равномерности. Ограничения (8) предотвращают одновременное нахождение поездов на станции более количества путей с пассажирскими платформами. Ограничения (9) отражают соблюдение интервала между последовательными выездами/въездами поездов.
Оценки равномерности распределения событий станций (5) и перегонов (6) в интервале расписания сети формируют множество первых и вторых векторных компонент равномерности маршрутов на очередном шаге оптимизации начального расписания
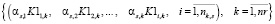 , (10)
, (10)
где 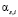 – коэффициент важности оценки,
– коэффициент важности оценки, 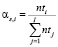 ;
;
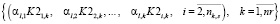 , (11)
, (11)
где 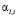 – коэффициент важности оценки,
– коэффициент важности оценки,
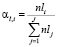 .
.
Необходимо отметить, что
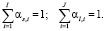
Многокритериальное ранжирование векторов (10) и (11) порождает множества рангов маршрутов по равномерности станций и перегонов
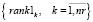 , (12)
, (12)
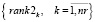 . (13)
. (13)
Ранги (12, 13) формируют множество векторов (критериев равномерности) маршрутов
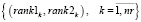 . (14)
. (14)
Старший по рангу маршрут, полученный многокритериальным ранжированием векторов (14), является самым неравномерным при принятых оценках и критериях равномерности. Он становится очередным кандидатом 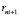 на перестановку в расписании.
на перестановку в расписании.
Для определения времени отправления с начальной станции 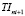 поездов маршрута
поездов маршрута 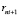 циклично выполняются следующие действия:
циклично выполняются следующие действия:
для 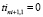 с шагом = 0,1 часа до 24 часов определение значений оценок (5, 6) для перегонов и станций маршрута с накоплением множеств векторов с учетом ограничений (8, 9):
с шагом = 0,1 часа до 24 часов определение значений оценок (5, 6) для перегонов и станций маршрута с накоплением множеств векторов с учетом ограничений (8, 9):
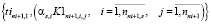 , (15)
, (15)
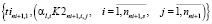 . (16)
. (16)
Многокритериальные ранжирования векторов (15, 16) формируют множества векторов рангов для начальных времен движения поездов маршрута 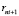 :
:
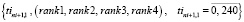 . (17)
. (17)
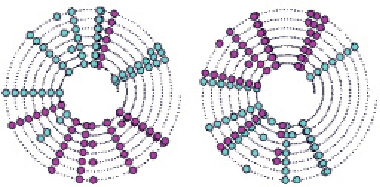
Рис. 1. Расписания въезда/выезда с перегона на граничные станции:  – выезд на перегон;
– выезд на перегон;  – въезд на станцию
– въезд на станцию
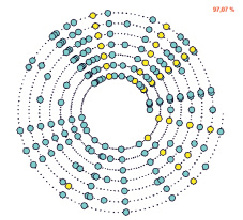
Рис. 2. Расписание въезда поездов на станцию:  – с одного перегона;
– с одного перегона;  – двух поездов с разных перегонов
– двух поездов с разных перегонов
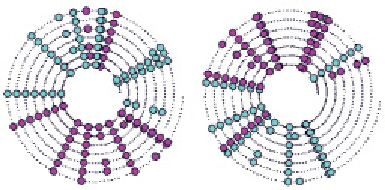
Рис. 3. Расписания въезда/выезда с перегона на граничные станции
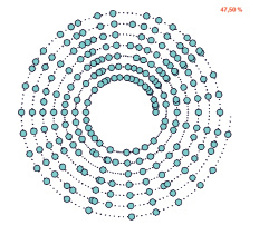
Рис. 4. Расписание въезда поездов на станцию
Многокритериальное ранжирование векторов (17) определяет начальное время 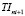 движения поездов маршрута
движения поездов маршрута 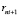 в оптимизированном расписании железнодорожной сети.
в оптимизированном расписании железнодорожной сети.
Для проверки корректности предлагаемых решений разработано тестовое задание для пассажирского железнодорожного транспорта. Задание включает три группы элементов, описывающих структуру железнодорожной сети, маршруты следования поездов и периодичность отправления поездов. В задании содержится 100 станций, 128 перегонов и заявки для 471 поезда 100 маршрутов в неделю. Предложенные методы реализованы в среде СУБД Access средствами встроенного языка программирования.
На рис. 1 и 2 представлены визуализированные результаты формирования начального расписания железнодорожной сети для самого загруженного перегона и станции [3].
Для расписаний станций и перегонов использованы представления, в которых спираль является осью времени с отсчетом от ее начала, а длина спирали соответствует интервалу расписания [4]. Виток спирали – наименьший период расписания. Пометками на спирали фиксируется прибытие/отправление транспортного средства. На рис. 2 в верхнем правом углу указано среднеквадратичное отклонение событий расписания станции в %.
На рис. 3 и 4 представлены результаты оптимизации начального расписания железнодорожной сети для тех же перегона и станции.
Сопоставление рис. 2 и 4 показывает более чем двукратное улучшение среднеквадратичного отклонения событий станции. Сопоставление рис. 1 и 3 менее оптимистично с визуальной точки зрения.
Авторы считают, что в данной работе новыми являются следующие положения и результаты:
- осуществлена формализация задачи формирования транспортного расписания;
- представлены подходы и алгоритмы задач формирования расписаний пассажирских поездов дальнего следования на основе методов ранжирования теории принятия решений;
- разработана информационная система формирования транспортного расписания для решения различных задач тактического и оперативного уровней планирования;
- представлены результаты формирования расписаний пассажирских поездов дальнего следования средствами информационной системы.



