Рассмотрим пример системы дифференциальных уравнений цилиндрической оболочки ракеты – системы обыкновенных дифференциальных уравнений 8-го порядка (после разделения частных производных методом Фурье). Система линейных обыкновенных дифференциальных уравнений имеет вид
,
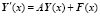где Y(x) – искомая вектор-функция задачи размерности 8х1,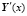 
– производная искомой вектор-функции размерности 8х1, A – квадратная матрица коэффициентов дифференциального уравнения размерности 8х8, F(x) – вектор-функция внешнего воздействия на систему размерности 8х1. Здесь и далее векторы обозначаем жирным шрифтом вместо черточек над буквами. Краевые условия имеют вид
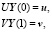
где Y(0) – значение искомой вектор-функции на левом крае х = 0 размерности 8х1, U – прямоугольная горизонтальная матрица коэффициентов краевых условий левого края размерности 4х8, u – вектор внешних воздействий на левый край размерности 4х1, Y(1) – значение искомой вектор-функции на правом крае х = 1 размерности 8х1, V – прямоугольная горизонтальная матрица коэффициентов краевых условий правого края размерности 4х8, v – вектор внешних воздействий на правый край размерности 4х1. В случае, когда система дифференциальных уравнений имеет матрицу с постоянными коэффициентами A = const, решение задачи Коши имеет вид [10]:
,
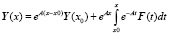где
,
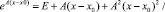
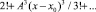где E – это единичная матрица.
Матричная экспонента ещё может называться матрицей Коши или матрициантом и может обозначаться в виде
.
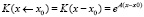Тогда решение задачи Коши может быть записано в виде:
,
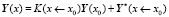где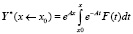 
это вектор частного решения неоднородной системы дифференциальных уравнений.
Из теории матриц [2] известно свойство перемножаемости матричных экспонент (матриц Коши):
.
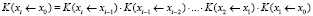В случае, когда система дифференциальных уравнений имеет матрицу с переменными коэффициентами A = A(x), решение задачи Коши предлагается, как это известно, искать при помощи свойства перемножаемости матриц Коши. То есть интервал интегрирования разбивается на малые участки и на малых участках матрицы Коши приближенно вычисляются по формуле для постоянной матрицы в экспоненте. А затем матрицы Коши, вычисленные на малых участках, перемножаются:
,
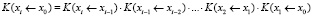где матрицы Коши приближенно вычисляются по формуле
,
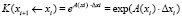где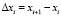 
.
Рассмотрим метод «переноса краевых условий» (прямой вариант метода) для решения краевых задач с нежесткими обыкновенными дифференциальными уравнениями. Предлагается выполнять интегрирование по формулам теории матриц [2] сразу от некоторой внутренней точки интервала интегрирования к краям:
,
.
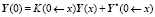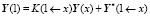Подставим формулу для Y(0) в краевые условия левого края и получим
,
,
.
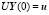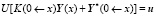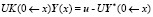Аналогично для правых краевых условий получаем
,
,
.
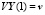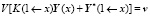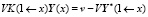То есть получаем два матричных уравнения краевых условий, перенесенные в рассматриваемую точку x:
,
.
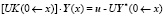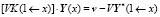Эти уравнения перенесенных краевых условий с прямоугольными горизонтальными матрицами коэффициентов объединяются в одну систему линейных алгебраических уравнений с квадратной матрицей коэффициентов для нахождения решения Y(x) в любой рассматриваемой точке x:
.
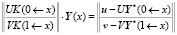Рассмотрим метод «переноса краевых условий» (пошаговый вариант метода) для решения краевых задач с жесткими обыкновенными дифференциальными уравнениями. Полное решение системы дифференциальных уравнений имеет вид
.
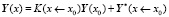Или можно записать
.
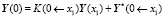Подставляем это выражение для Y(0) в краевые условия левого края и получаем
,
,
.
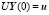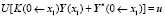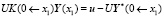Или получаем краевые условия, перенесенные в точку x1:
,
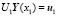где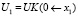 
и 
.
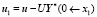Далее запишем аналогично
.
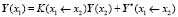И подставим это выражение для Y(x1) в перенесенные краевые условия точки x1:
,
,
.
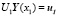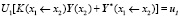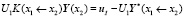Или получаем краевые условия, перенесенные в точку x2:
,
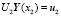где
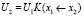
и
.
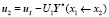И так в точку x* переносим матричное краевое условие с левого края и таким же образом переносим матричное краевое условие с правого края. Покажем шаги переноса краевых условий правого края. Можем записать
.
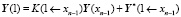Подставляем это выражение для Y(1) в краевые условия правого края и получаем
,
,
.
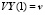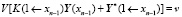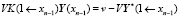Или получаем краевые условия правого края, перенесенные в точку xn –1:
,
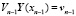где
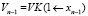
и
.
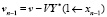Далее запишем аналогично
.
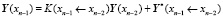И подставим это выражение для Y(xn –1) в перенесенные краевые условия точки xn –1:
,
,
.
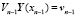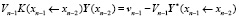Или получаем краевые условия, перенесенные в точку xn –2:
,
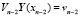где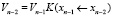 
и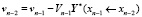 
.
И так во внутреннюю точку x* интервала интегрирования переносим матричное краевое условие, как показано, и с левого края и таким же образом переносим матричное краевое условие с правого края и получаем
, 
.
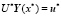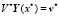Из этих двух матричных уравнений с прямоугольными горизонтальными матрицами коэффициентов очевидно получаем одну систему линейных алгебраических уравнений с квадратной матрицей коэффициентов:
.
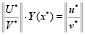Известны формулы ортонормирования систем линейных алгебраических уравнений [2]. В случае «жестких» дифференциальных уравнений предлагается применять построчное ортонормирование матричных краевых условий в процессе их переноса в рассматриваемую точку [3, 5]. То есть, получив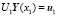 
, применяем к этой группе линейных алгебраических уравнений построчное ортонормирование и получаем эквивалентное матричное краевое условие: U1ортоY(x1) = u1орто. И теперь уже в это проортонормированное построчно уравнение подставляем
.
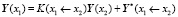И получаем
,
.
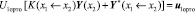Или получаем краевые условия, перенесенные в точку x2:
,
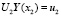где
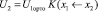
и
.
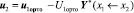Теперь уже к этой группе линейных алгебраических уравнений применяем построчное ортонормирование и получаем эквивалентное матричное краевое условие:
.
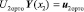И аналогично поступаем с промежуточными матричными краевыми условиями, переносимыми с правого края в рассматриваемую точку. В итоге получаем систему линейных алгебраических уравнений с квадратной матрицей коэффициентов, состоящую из двух независимо друг от друга поэтапно проортонормированных матричных краевых условий, которая решается методом Гаусса с выделением главного элемента для получения решения Y(x*) в рассматриваемой точке x*:
.
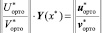Вместо формулы для вычисления вектора частного решения неоднородной системы дифференциальных уравнений в виде [5]
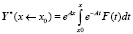
предлагается использовать следующую формулу для каждого отдельного участка интервала интегрирования:
.
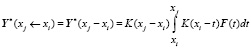Правильность приведенной формулы подтверждается следующим:
,
,
.
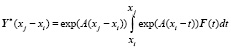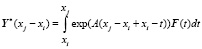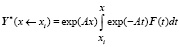Вычисление вектора частного решения системы дифференциальных уравнений производится при помощи представления матрицы Коши под знаком интеграла в виде ряда и интегрирования этого ряда поэлементно:
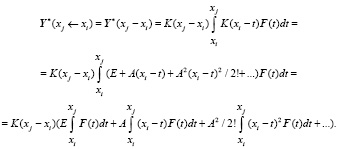
Эта формула справедлива для случая системы дифференциальных уравнений с постоянной матрицей коэффициентов A = const.
Рассмотрим вариант, когда шаги интервала интегрирования выбираются достаточно малыми, что позволяет рассматривать вектор F(t) на участке (xj – xi) приближенно в виде постоянной величины F(xi) = constant, что позволяет вынести этот вектор из-под знаков интегралов:
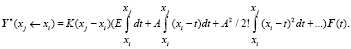
Известно, что при T = (at + b) имеем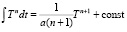 
(при n ≠ –1).
В нашем случае имеем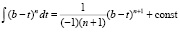 
(при n ≠ –1).
Тогда получаем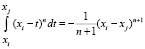 
.
Тогда получаем ряд для вычисления вектора частного решения неоднородной системы дифференциальных уравнений на малом участке (xj – xi):
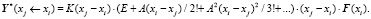
Для случая дифференциальных уравнений с переменными коэффициентами для каждого участка может использоваться осредненная матрица Ai =A(xi) коэффициентов системы дифференциальных уравнений. Если рассматриваемый участок интервала интегрирования не мал, то предлагаются следующие итерационные (рекуррентные) формулы. Приведем формулы вычисления вектора частного решения, например,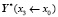 
на рассматриваемом участке 
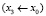через векторы частного решения 
, 
, 
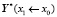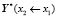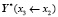соответствующих подучастков 
, 
, 
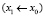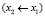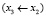. Имеем 
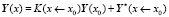. Также имеем формулу для отдельного подучастка:
.
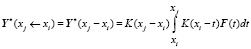Можем записать
,
.
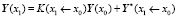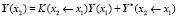Подставим Y(x1) в Y(x2) и получим
.
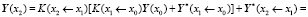
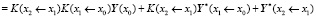Сравним полученное выражение с формулой
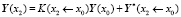
и получим, очевидно, что
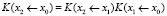
и для частного вектора получаем формулу
.
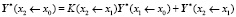То есть вектора подучастков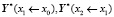 
не просто складываются друг с другом, а с участием матрицы Коши подучастка. Аналогично запишем 
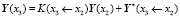и подставим сюда формулу для Y(x2) и т.д.:
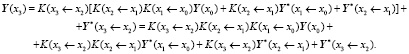
Сравнив полученное выражение с формулой
,
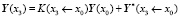очевидно, получаем, что
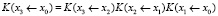
и вместе с этим получаем формулу для частного вектора:
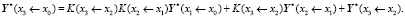
То есть именно так и вычисляется частный вектор – вектор частного решения неоднородной системы дифференциальных уравнений, то есть так вычисляется, например, частный вектор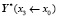 
на рассматриваемом участке 
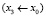через вычисленные частные вектора 
, 
, 
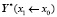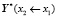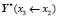соответствующих подучастков 
, 
, 
.
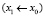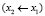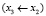Взято из [2]. Пусть дана система линейных алгебраических уравнений порядка n: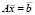 
. Здесь над векторами (как в первоисточнике) поставим черточки вместо их обозначения жирным шрифтом. Будем рассматривать строки матрицы A системы как векторы:
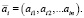
Ортонормируем эту систему векторов. Первое уравнение системы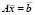 
делим на 
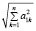. При этом получим
,
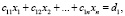
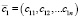где
, 
, 
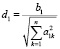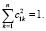
Второе уравнение системы заменяется на
,
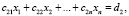
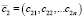где
, 
,
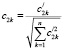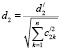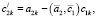
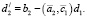
Аналогично поступаем дальше. Уравнение с номером i примет вид
,
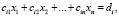
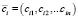где
, 
,
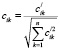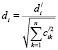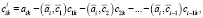
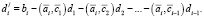
Процесс будет осуществим, если система линейных алгебраических уравнений линейно независима. В результате мы придем к новой системе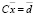 
, где матрица C будет с ортонормированными строками, то есть обладает свойством 
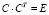, где E – это единичная матрица.
Уточнены формулы метода Виноградовых переноса краевых условий. Изложение выполнено так, что оно достаточно для выполнения программирования без необходимости получать матричные формулы из других источников. Изложенные формулы проверены расчетами тонкостенных оболочек вращения, в частности цилиндрической и сферической оболочек. Результаты проверочных расчетов совпали с результатами другого известного метода Виноградовых для решения жестких краевых задач. В ракетно-космической отрасли данный метод позволяет устранить известные сложности, связанные с проведением многопараметрического вычислительного процесса решения краевых задач. классическими методами и тем самым значительно сократить затраты расчетного времени. Следует отметить, что движение космического аппарата на активном участке, как правило, осуществляется с использованием заранее рассчитанной и заложенной в бортовой компьютер программы изменения вектора тяги двигательной установки по времени. Вместе с тем разработанный метод может быть положен в основу создаваемых адаптивных бортовых алгоритмов, позволяющих оперативно вносить коррекции в программу управления в зависимости от значений текущих параметров движения космического аппарата.