Главной задачей обучения специалистов на сегодняшний день является то, что теоретические и практические знания, полученные студентами в вузе, находили максимальное применение в их профессиональной деятельности. В век информационных технологий, когда объем информации с каждым днем увеличивается, ее невозможно усвоить за годы обучения в школе, а в дальнейшем и в вузе, если не найти новые подходы по методике обучения [7]. Основную нагрузку в этом направлении несут школы, так как на знаниях и умениях, закладываемых в средней школе, опирается обучение в вузе.
Не секрет, что физика является одной из самых сложных дисциплин в школе.
На сегодняшний день актуальна разработка новых технологий в преподавании физики в связи с введением федерального государственного образовательного стандарта (ФГОС) второго поколения. ФГОС нового поколения содержит системные обновления, которые касаются целей образования, его содержания и структуры, системы оценивания и технологий обучения [9].
Основной задачей обучения являются получение новых знаний в рамках учебного предмета и по их преобразованию и применению в учебно-исследовательской и проектной деятельности формирование научного типа мышления, способность к решению учебно-практических и учебно-познавательных задач, к самостоятельному поиску методов решения практических задач. Необходимо развивать у учащихся способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников.
И одним из ключевых моментов в этом направлении является решение физических задач в средней школе, т.к. решение задач позволяет понять и запомнить основные законы и формулы физики, развивает у учащихся навыки в использовании общих физических законов для решения конкретных задач, имеющих практическое применение.
Очевидно, что умение решать задачи является одним из главных критериев оценки усвоения программного материала. Основной проблемой при изучении физики в средней школе является неумение применять учениками теорию к решению задач, что является существенным пробелом в методике физического образования школ.
Целью данной работы является выработать единый «алгоритмический» подход к решению задач по механике.
Приведем основные принципы, без которых невозможно научить решать физические задачи:
1. Знание теоретического материала по данной теме, т.е.определения всех физических величин, их единиц измерения, формулировки законов физики и их запись в виде формул.
2. Умение проводить анализ задачи и выстраивать логическую цепочку исследуемых законов и понятий.
3. Хорошее владение математическим аппаратом.
Мы счиатем основной ошибкой при обучении физике требование в заучивании формул и определений. Теория должна запоминаться при её применении, либо при решении задач, либо при выполнении практических и лабораторных работ. Если у учащегося создается представление о физике как о предмете с огромным набором формул и определений, который невозможно запомнить, то такой подход к обучению физике в корне разрушает творческие способности учащихся и, кроме вреда такое обучение ничего не дает.
Основная методическая ошибка, которую допускают учащиеся, приступая к решению задач, это то, что они заостряют внимание на искомой величине и начинают записывать формулы, где искомая величина записывается через другие, дальше записывают очередные формулы, которые входят в исходную и.т.д. В итоге получается нагромождение формул, и чаще всего решение заходит в тупик.
Правильный подход к решению задачи состоит в том, что необходимо сначала проанализировать задачу, исходя из основных определений и законов физики, и текстовое условие задачи записать в виде математических соотношений [1, 2, 4]. Решение практически любой физической задачи состоит из трех этапов:
1. Физический.
Записать основные законы физики, необходимые для решения данной задачи, составив для них математические соотношения.
2. Математический.
Решение полученных уравнений для нахождения искомой величины.
3. Проверка размерности полученной физической величины и достоверности конечного результата.
По возможности эти этапы должны быть разделены. Например на первом этапе нежелательно начинать проводить математические преобразования и расчеты, здесь необходимо сосредоточиться на законах физики, которые следует применять для решения конкретной задачи, и применить алгоритм её решения и только после этого приступать к математичеким преобразованиям и расчетам. Получив расчетную формулу, необходимо проанализировать ее, что расширяет представление о рассматриваемом явлении. Задачу можно считать решенной только после третьего этапа.
Приведем общий алгоритм решения задач по физике, который мы будем конкретизировать в дальнейшем изложении для различных разделов физики.
Алгоритм решения задач по физике
1. Внимательно прочитать условие задачи.
2. Записать данные задачи с помощью общепринятых буквенных обозначений в системе СИ.
3. При необходимости выполнить рисунки или чертежи задачи.
4. Записать основные уравнения и законы, необходимые для решения конкретной задачи.
5. Найти решение в общем виде, выразив искомые величины через заданные.
6. Проверить правильность решения задачи в общем виде.
7. Произвести вычисления и проверить размерность.
8. Произвести оценку реальности полученного решения.
9. Записать ответ.
Кинематика равнопеременного движения
Основной подход к решению задач по кинематике равнопеременного движения состоит в записи уравнений движения применительно к условию конкретной задачи:
; 
; 
,
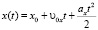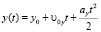
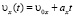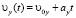где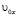 
и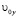 
– проекции начальной скорости на оси x и y соответственно, ax и ay – проекции ускорения на оси x и y соответственно.
Записанные уравнения являются основными уравнениями кинематики, и их использование достаточно, чтобы решить любую задачу кинематики равномерного и равнопеременного движения [6, 8].
Приведем алгоритм решения задач по кинематике.
1. Дано. СИ.
2. Выбрать тело отсчета, систему координат, изобразить траекторию движения материальной точки.
3. Определить вид движения и написать кинематические уравнения для координаты (и скорости) движения вдоль каждой оси.
4. Спроецировать записанные уравнения на оси координат.
5. Решить полученную систему уравнений.
6. Произвести вычисления и проверить размерность.
7. Записать ответ.
Рассмотрим две задачи разных уровней сложности и применим к ним единый алгоритм решения задач.
Задача средней сложности [3]
Небольшой камень, брошенный с ровной горизонтальной поверхности земли под углом 30 градусов к горизонту, упал обратно на землю в 86,6 м от места броска. Какой максимальной высоты он достиг за время полета?
Физический этап решения
1) Дано: S = 86,6 м; α = 30 °
Найти: h.
2) Выберем тело отсчета и систему координат (рис. 1).
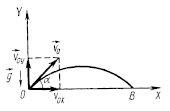
Рис. 1
3) Запишем кинематические уравнения для координат вдоль каждой оси:
; 
.
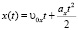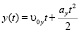4) Спроецируем записанные уравнения на оси координат:
; 
.
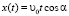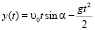Математический этап решения
5) Решаем полученную систему уравнений.
Из условия y = 0 получаем время полета:
,
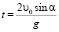подставляя полученное выражение в уравнение движения для x(t) и y(t) с учетом того, что при падении
; 
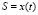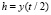
для максимальной дальности полета и максимальной высоты подъема, получаем
; 
.
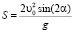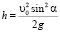Поделив h на S, получим расчетную формулу
.
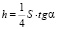Расчет и проверка размерности полученной физической величины.
6) 
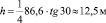[h] = [м]
7) ответ: 12,5 м.
Задача повышенной сложности [5]
На крышу дома высотой h с расстояния l от него мальчик хочет забросить мяч (рис. 2). Каково минимальное значение начальной скорости мяча для такого броска?
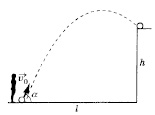
Рис. 2
Физический этап решения
1) Дано: h, l
Найти: ν0.
2) Выберем тело отсчета и систему координат (рис. 3).
3) Запишем кинематические уравнения для координат вдоль каждой оси:
; 
.
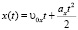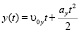4) Спроецируем записанные уравнения на оси координат:
;
.
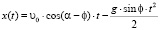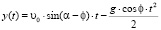Запишем дополнительные условия
; 
.
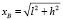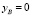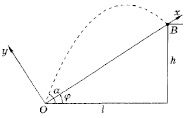
Рис. 3
Математический этап решения
5) Решаем полученную систему уравнений.
Из условия yВ = 0 получаем время полета:
,
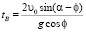подставляя полученное выражение в уравнение движения для x(t) с учетом того, что
,
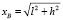получаем выражение для начальной скорости в виде
.
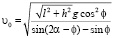Т.к. по условию задачи скорость должна быть минимальной, то
,
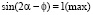и окончательный результат для минимальной скорости после несложных математических преобразований записывается в виде
.
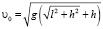Проверка размерности полученной физической величины
6) 
;
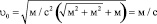7) ответ: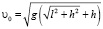 
.
Как видим, из рассмотренных примеров данный алгоритм позволяет решать задачи по кинематике разных уровней сложности по единому алгоритму, что поможет учащимся при решении практически любой задачи по кинематике.