На сегодняшний день к электрогенерирующему оборудованию предъявляются всё более высокие требования по эксплуатационной надежности, при этом большое значение приобретают меры по предупреждению и раннему обнаружению дефектов средствами технической диагностики. В тоже время современные средства цифровой обработки информации дают возможность проектировать новые чувствительные устройства технической диагностики крупных синхронных генераторов [1, 2, 5–8], способные достоверно выявлять сложные дефекты на ранней стадии их развития, что оправдывает любые затраты на их разработку. В ряде устройств [3, 9, 10, 13] диагностики повреждений межвитковой изоляции обмотки ротора, требуется разработка специфического фильтра, которому необходимо качественно выделить гармоническую с частотой равной частоте вращения машины из однополярного сигнала на выходе магнитометрического датчика.
Целью данной работы является синтез оптимального цифрового фильтра, способного качественно выделить полезный сигнал, и разработка методики настройки параметров проектируемого фильтра.
Постановка задачи
Для реализации устройства диагностики синхронной электрической машины необходимо синтезировать фильтр, способный качественно выделить полезный гармонический сигнал с частотой fv = f1/p, где f1 – частота сети, p – число пар полюсов. При этом основными паразитными компонентами сигнала выступает постоянная составляющая, гармоническая с частотой 2fv, а также посторонние шумы [4]. Разработать методику настройки фильтра.
Способ диагностики базируется на анализе сигнала ЭДС с выхода магнитометрического датчика, установленного в торцевой зоне синхронной электрической машины рис. 1, а.
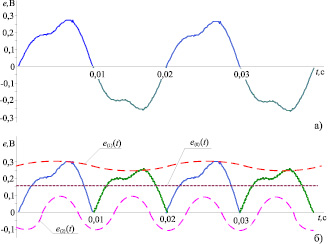
Рис. 1. Сигнал ЭДС на выходе магнитометрического датчика
Анализ кривой выпрямленного значения ЭДС показывает, что при витковом замыкании в обмотке явнополюсного ротора с числом пар полюсов p = 1 в выпрямленном сигнале, помимо постоянной и 100 Гц составляющей, появляется огибающая с частотой, равной частоте вращения машины (50 Гц) – рис. 1, б. Полезной информацией о наличии виткового замыкания является появление в выпрямленном сигнале частоты fv = f1/p, где f1 – частота сети.
Способ построения диагностической системы [1, 2, 5–8] заключается в том, что измеренный электрический сигнал ЭДС с выхода магнитометрического датчика, установленного в торцевой зоне синхронной электрической машины, преобразуют в однополярный, из которого затем выделяют гармоническую с частотой fv = f1/p. Если она превысит установленную величину, то это воспринимают как сигнал о наличии виткового замыкания в обмотке ротора синхронной машины.
Очевидно, что основным элементом устройства диагностики выступает фильтр, способный с минимальными потерями выделить полезный сигнал с частотой fv, например, для системы диагностики синхронной машины с частотой вращения 3000 об/мин это будет частота равная 50 Гц. Фильтр должен максимально подавить частоту 2fv, для данного типа машины это частота 100 Гц. Особенностью работы данного фильтра является сверхмалое расстояние между частотами fv и 2fv, составляющее всего одну октаву, поэтому в данном случае нецелесообразно использование стандартной методики его настройки. Поскольку паразитной частотой является всего одна гармоническая 2fv, то при синтезе фильтра ставилось не использовать комбинацию фильтров высоких и низких частот для формирования полосно-пропускающего фильтра, а использовать характерные локальные неоднородности амплитудно-частотные характеристики (АЧХ) цифрового рекурсивного фильтра. Тип фильтра определялся из анализа АХЧ наиболее известных фильтров: Баттерворта, Чебышева I рода, Чебышева II рода и Кауэра.
На рис. 2 представлены АЧХ анализируемых цифровых фильтров. Использование фильтра Баттерворта (линия 2 (синяя)), является одним из худших вариантов. Он значительно подавляет полезную гармоническую составляющую ΔБ.(fv) и слабо подавляет «паразитную» гармоническую составляющую с частотой 2fv – ΔAБ.(2fv). Фильтр Чебышева I рода (линия 1 (зелёная)), минимально подавляет сигнал с частотой fv ΔAЧ.I(fv), но при этом подавляет слабее фильтра Баттерворта паразитную гармоническую с частотой 2fv ΔAЧ.I(2fv). Фильтр Чебышева II рода (линия 3 (оранжевая)) отлично подавляет гармонику с частотой 2fv ΔAЧ.II(2fv), однако он имеет самый высокий уровень ослабления полезного сигнала с частотой fv ΔAЧ.II(fv). Как видно из рис. 1, АЧХ эллиптического фильтра (линия 4 (красная)) является наилучшей по критерию пропускания и подавления.
Как видно из анализа АХЧ эллиптического фильтра (рис. 3), для поставленной задачи целесообразно использовать при настройке фильтра локальные неоднородности АХЧ.
Передаточная функция эллиптического фильтра имеет два варианта записи [14, 15]. Для четного порядка фильтра
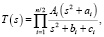
для нечетного порядка фильтра
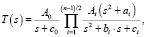
где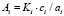 
; Ki – коэффициент усиления; ai, bi, ci, c0 – табличные значения параметров эллиптического фильтра, приведенные в [10].
АЧХ эллиптического фильтра низких частот имеет пульсации, как в полосе пропускания, так и в полосе подавления (рис. 3).
При настройке параметров эллиптического фильтра по стандартной методике [14, 15] принято использование следующих обозначений:
– неравномерность передачи в полосе пропускания (PRW), дБ, равна
PRW = – 20 log10А1, (1)
где А1 – нижняя граница предельно допустимой неравномерности АЧХ в полосе пропускания.
– минимальное затухание в полосе подавления (MSL), дБ, равное
MSL = – 20 log10А2, (2)
где А2 – верхняя граница предельно допустимой неравномерности АЧХ в полосе подавления.
– ширина переходной области TW, которая в нашем случае составляет
TW = 2fv – fv (3)
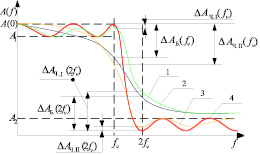
Рис. 2. Амплитудно-частотные характеристики рекурсивных фильтров: 1 – АЧХ фильтра Чебышева I рода; 2 – АЧХ фильтра Баттерворта; 3 – АЧХ фильтра Чебышева II рода; 4 – АЧХ эллиптического фильтра
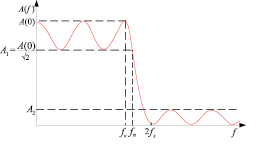
Рис. 3. Амплитудно-частотная характеристика эллиптического фильтра низких частот
Для заданных значений PRW и MSL повышение порядка приводит к увеличению числа пульсации в полосах пропускания и подавления и уменьшению TW.
Согласно [14] передаточная функция эллиптического фильтра по форме идентична передаточной функции фильтра Чебышева [15]. Постоянные параметры ai, bi, ci, c0, которые отличаются от параметров инверсного фильтра Чебышева, вычисляются крайне сложно, поскольку процесс вычисления требует знания эллиптических Якоби [14]. Потому следует использовать стандартные настройки эллиптического фильтра при фиксированных значениях PRW. В [14] приведены таблицы коэффициентов ai, bi, ci, c0, соответствующие различным величинам неравномерности передачи в полосе пропускания PRW = 0,1 дБ; 0,5 дБ; 1 дБ; 2 дБ; 3 дБ.
Если выбрать PRW = 3 дБ и нанести на ось ординат АЧХ соответствующее ей значение А1, то на оси частот получим величину fп – граничную частоту полосы пропускания эллиптического ФНЧ (рис. 3).
Учитывая все вышесказанное, настройку фильтра предлагается производить таким образом, чтобы максимальный коэффициент передачи соответствовал частоте fv = 50 Гц. Также для настройки фильтра воспользуемся еще одной его особенностью – в полосе подавления имеются точки минимума. Поэтому вторым критерием настройки фильтра предлагается настройка на минимальный коэффициент усиления в полосе подавления частоты 2fv = 100 Гц (рис. 3).
Настройка фильтра производится в следующем порядке:
1. Определить значение коэффициента ai как отношение основной несущей частоты к частоте fv:
.
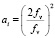2. Производим уточнение коэффициента ai по таблице [10] и из таблицы определяем остальные коэффициенты фильтра.
3. Определяем граничную частоту полосы пропускания fп такой, которая будет обеспечивать совпадение fv с частотой ближайшего максимума полосы пропускания fmax.
4. Производим уточнение частоты, соответствующей максимальному коэффициенту усиления:
.
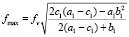5. Строим амплитудно-частотную характеристику.
Блок-схема алгоритма расчета эллиптического фильтра представлена на рис. 4.
По вышеприведенной методике произведем расчет эллиптического фильтра при работе генератора на сеть с частотой 50 Гц:
1. Определим, каким должен быть коэффициент ai по формуле
.
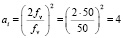2. Минимальный порядок эллиптического фильтра, который имеет коэффициент ai является третий. Принимаем эллиптический фильтр третьего порядка со следующими параметрами:
a1 = 3,611302; b1 = 0,253951; c1 = 0,873882; c0 = 0,0335021.
3. Принимаем граничную частоту полосы пропускания fп = 56 Гц, которая будет обеспечивать совпадение fv = 50 Гц с частотой ближайшего максимума полосы пропускания fmax = fv.
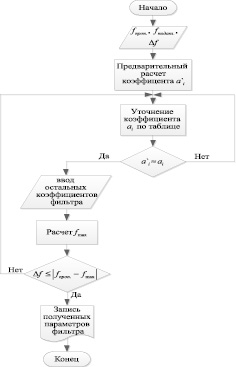
Рис. 4. Блок-схема алгоритма расчета эллиптического фильтра
4. Произведем расчет частоты, соответствующей максимальному коэффициенту усиления:
.
Для настройки устройства был смоделирован тестовый сигнал, состоящий из пяти частей: низкий нормальный сигнал (полуволны симметричны), полуволны отличаются на 1,5 %, участок роста полуволн (имитация переходного процесса), высокий сигнал с разницей амплитуд полуволн в 1,5 %, высокий нормальный сигнал. Устройство диагностики достоверно срабатывало при разнице полуволн в 1,5 % и выше, что говорит о качественном выделении фильтром полезной гармонической и способности устройства диагностики выявлять замыкание одного и более витка в обмотке ротора у синхронных машин средней и большой мощности.
Заключение
В результате сопоставительного анализа амплитудно-частотных характеристик наилучшим по качеству выделения требуемой гармонической определен фильтр Кауэра. Разработана методика расчета параметров эллиптического фильтра с учетом локальных неоднородностей амплитудно-частотной характеристики, позволяющая минимизировать потери полезного сигнала и максимально подавить паразитную частоту.