Моделирование поведения дискретных многомассовых виброударных систем возникает в различных областях науки и техники. Примерами могут служить устройство для вибрационного транспортирования сыпучей среды, виброразгрузка сыпучих грузов из железнодорожных вагонов, вибросепарация, виброперемещение, виброгрохоты, виброизмельчение, а также технологии виброударного упрочнения [2].
В настоящее время моделирование сложных виброударных систем осуществляют на суперкомпьютерах, которые представляют собой большое число высокопроизводительных серверных компьютеров, соединённых друг с другом локальной высокоскоростной магистралью для достижения максимальной производительности, в рамках подхода распараллеливания вычислительной задачи. В то же время продолжительность моделирования рассматриваемых виброударных систем на персональных компьютерах занимает от 2 часов и выше.
В данной работе предлагается создать специальный метод исследования многомассовых виброударных систем с распараллеливанием вычислений на графических процессорах NVIDIA с использованием технологии CUDA [1] для ускорения результатов моделирования и их оперативного отображения.
Достоинством метода является возможность проведения моделирования оператором производства на портативном ПК продолжительностью от 25 мин, для оперативного получения технологических параметров исследуемой системы.
В исследуемой работе в качестве частного случая двумерной многомассовой системы выступает технология виброударного упрочнения и виброабразивной обработки, широко применяемая в современном машиностроении для финишной обработки деталей различной формы.
Рассматриваемая последовательная программа моделирования исследования двумерной многомассовой динамической системы с распределенными параметрами реализована в среде Delphi [3,5]. Компилятор nvcc (NVidia CUDA compiler) с поддержкой технологии CUDA для распараллеливания вычислений базируется на языке С++ со специальными расширениями для написания кода для GPU [4]. Он встраивается в пакет Microsoft Visual Studio и участвует в раздельной компиляции исходных файлов. В связи с этим необходимо реализовать функции с распараллеливанием в виде динамической библиотеки, а затем вызывать их из программы на Delphi.
Для корректного взаимодействия программных платформ необходимо описать в С++ все необходимые структуры данных, используемых в Delphi. При описании типов в C++ необходимо следить за их выравниванием и размером – размеры соответствующих типов в C++ и Delphi должны совпадать.
При реализации программы моделирования технологии виброударного упрочнения все структуры данных создаются в заголовочном файле, содержащем описание каждого из типов используемых структур:
- fgranulprop – структура, используемая для описания каждой частицы ансамбля инструментальной среды, содержащая в себе свойства, не изменяющиеся во времени моделирования (диаметр, материал, масса, момент инерции);
- fgranulstate – структура, используемая для хранения текущего состояния частицы инструментальной среды (позиция, скорость, угловая скорость, фаза);
- dynamictech – динамические параметры инструментальной среды (момент начала контакта, продолжительность контакта, угол соударения, скорость соударения, сила контакта, динамический коэффициент восстановления и т.д.);
- fspline – структура, содержащая информацию о сегменте сплайна границы в некоторый момент времени (точки начала и конца сегмента сплайна, номер следующего и предыдущего сегмента сплайна, его длина и т.д.);
- ffriction – структура, содержащая описание моделей трения для контакта сегмента сплайна с каждым типом частиц в ансамбле;
- Fcinematics – структура, описывающая кинематику материальной точки в одномерном пространстве, содержащая в себе ссылку на закон движения материальной точки, а также массив параметров, которые задаются по-разному, в зависимости от закона движения;
- Ftechparam – структура, содержащая технологические параметры детали (шероховатость, степень наклепа, глубина наклепа, остаточные напряжения, съем);
- Ftraectory – структура, описывающая траекторию поступательного движения материальной точки на плоскости, а также ее вращательное движение вокруг начала координат;
- Fsplineprop – структура, описывающая свойства группы сегментов сплайнов (траектория движения группы сегментов сплайнов, закон трения, дескриптор материала и т.д.);
- simParams – структура, описывающая саму систему для моделирования (центр области моделирования, размер ячейки области моделирования, количество сегментов сплайнов и др.).
Также в заголовочном файле определяются вспомогательные перечислимые типы, такие как:
- fmaterial – тип, содержащий имена материалов инструментальной среды и контейнера;
- fcinematictype – тип, содержащий законы движения групп сегментов сплайнов (гармоническая осцилляция, дельта – осцилляция).
В программе моделирования, созданной в среде Delphi, объявляются функции, реализованные в динамической библиотеке:
- Функция инициализации глобальных переменных моделирования в константной памяти графического процессора – InitSimParams.
- Функция, определяющая самое производительное из устройств графического процессора CUDA init_GP.
- Функция инициализации всех рабочих массивов системы частиц инструментальной среды в динамической библиотеке и глобальной памяти устройства InitParticleSystem.
- Функция инициализации сегментов сплайновой границы области в памяти устройства InitBoundary.
- Функция интегрирования, полностью выполняющаяся на графическом процессоре в динамической библиотеке Integrate_CUDA.
- Функция освобождения памяти ресурсов, выделенных под данные в динамической библиотеке – FreeDeviceResources().
Взаимодействие программных платформ Delphi и C++ в рамках распараллеливания вычислительных задач состоит из нескольких этапов. На первом этапе (рис. 1) программа, реализованная в среде разработки Delphi, создает экземпляр Solver класса TSolver, который вызывает при начале моделирования свой метод Initialize. Данный метод инициализирует динамические массивы и общие переменные: массы и размеры для пар частиц, текущую сплайновую границу, карту сил для сплайновой границы, кэш сегментов сплайнов (а). Также здесь происходит вызов CUDA_Initialize (б) из динамической библиотеки, которая инициализирует по отдельности общие параметры (в) (simParams, количество частиц инструментальной среды, временной шаг и т.д.), параметры системы частиц в виде еще нескольких массивов (г).
Второй этап – получение первых трех временных слоев в памяти центрального процессора, обозначаемого термином «хост», средствами программы из среды Delphi, посредством вызова метода WarmUp экземпляра Solver (рис. 2).
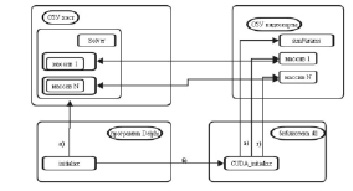
Рис. 1. Инициализация данных
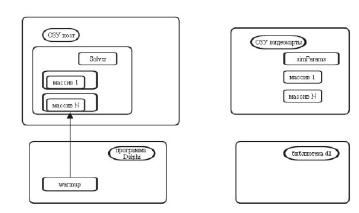
Рис. 2. Процедура разгонки системы
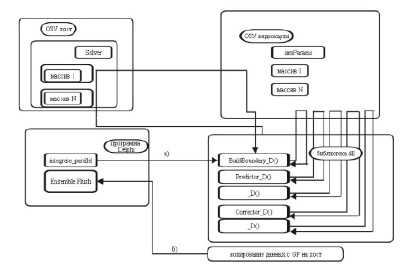
Рис. 3. Интегрирование системы
На следующем этапе в программе, реализованной в среде Delphi, процедура Integrate_Parallel класса TSolver, которая определяет текущий момент времени интегрирования системы, а затем из динамической библиотеки вызывает функцию интегрирования Integrate_CUDA(а), параметрами которой являются количество шагов и начальный момент времени. Функция Integrate_CUDA состоит из последовательно вызываемых функций BuildBoundary_D, Predictor_D, _D, Corrector_D, каждая из которых реализована с распараллеливанием вычислений на основе применения многоядерных параллельных вычислительных устройств и 3D-видеокарт на базе программно-аппаратной платформы NVidia CUDA. В завершение данного этапа происходит копирование данных в ОЗУ хоста (б). Очень важным является то, что копирование данных происходит в ту область хоста, где расположены данные экземпляра TSolver (рис. 3).
На заключительном этапе взаимодействия двух описанных сред разработки осуществляется очищение памяти хоста из программы, реализованной в среде Delphi путем вызова процедуры Utilize класса TSolver, которая освобождает память, выделенную под массивы данных в ОЗУ, а затем вызывает функцию FreeDeviceResources() из динамической библиотеки, освобождающую память под массивы данных на графическом процессоре.
В настоящей работе исследовались контейнеры с числом сегментов сплайнов в диапазоне от 200 до 800 и числом частиц инструментальной среды в диапазоне от 500 до 10000. Для исключения влияния формы контейнера и детали на ускорение вычислений были рассмотрены контейнер и деталь круглой формы.
В результате анализа выявлено, что эффект сокращения времени увеличивается с ростом частиц инструментальной среды и максимальное значение сокращения времени моделирования в 17 раз наблюдается на моделях при 10000 частиц инструментальной среды.
Также проводилось исследование влияния числа сегментов сплайнов при одинаковом числе частиц инструментальной среды на ускорение процедуры моделирования.
На рис. 4 представлено время выполнения последовательной и параллельной программы моделирования (сек) в зависимости от частиц инструментальной среды. Последовательная программа выполнялась на персональном компьютере ЦП Intel Xeon x5675 3.1 GHz, параллельная – на этом же ПК с использованием видеокарты Nvidia GeForce 970.
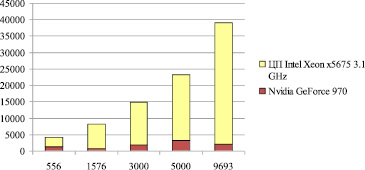
Рис. 4. Время моделирования системы в зависимости от количества частиц инструментальной среды
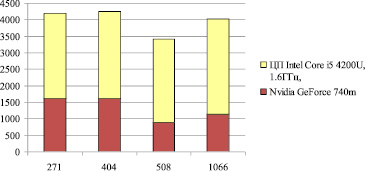
Рис. 5. Время моделирования системы в зависимости от количества сегментов сплайна при 500 частицах инструментальной среды
На рис. 5 представлено время выполнения последовательной и параллельной программы моделирования (сек) в зависимости от количества сегментов сплайна при 500 частицах инструментальной среды. Последовательная программа выполнялась на портативном компьютере ЦП Intel Core i5 4200U, 1.6ГГц, параллельная – на этом же ПК с использованием видеокарты Nvidia GeForce 740m.



