Технологической контроль процесса изготовления пропорциональных электромагнитов начинается с получения характеристики, содержащей информацию о технических параметрах, зависящих от режимов технологического процесса. Определение такой характеристики должно осуществляться на полностью собранном изделии и быть малозатратным с точки зрения времени и технических ресурсов. Такой интегральной характеристикой является динамическая характеристика намагничивания (ДХН) [1]. В работах [2, 4, 7] показано, что имея ДХН электромагнитного привода (рис. 1) можно рассчитать ряд характеристик, регламентированных ГОСТ [3]: статическую и динамическую тяговые характеристики F = f(δ) и Fд = f(δ), характеристики движения якоря δ = f(t) и изменение тока в обмотке во времени i = f(t).
После подачи питания ток в обмотке достигает значения тока трогания, которому соответствует точка 1. В это мгновение якорь приходит в движение, в процессе которого рабочий зазор d уменьшается, индуктивность обмотки растет, а ток в ней падает до тех пор, пока якорь не притянется к сердечнику, чему соответствует точка 2. Во время движения якоря связь между магнитным потоком Ф и током I определяется кривой 1–2.
По окончании движения якоря ток опять начинает возрастать, достигая установившегося значения в точке 3. После отключения питания электромагнита ток в обмотке падает и при достижении значения тока отпускания Iотп (точка 4) якорь приходит в движение, а рабочий зазор увеличивается от минимального δmin до максимального δmax. Точка 5 соответствует окончанию движения якоря электромагнита. Далее ток спадает до нуля, чему соответствует точка 6. Из-за остаточной намагниченности магнитопровода поток, соответствующий точке 6, больше нуля.
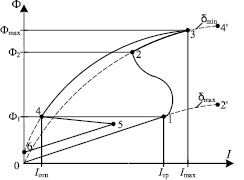
Рис. 1. ДХН электромагнитного привода
Динамическая характеристика намагничивания электромагнитного привода несет информацию о магнитных, электрических, тяговых и динамических свойствах пропорциональных электромагнитов, а для ее получения могут быть использованы так называемые «беcсенсорные» устройства [8]. При этом не требуется разборка испытуемого изделия и по рабочей обмотке протекают токи соответствующие номинальным.
Использование ДХН в виде массива пар точек магнитный поток ток для дальнейшей обработки затруднительно. Большой объем данных (одна ДХН, измеренная с погрешностью до 3 %, содержит порядка 15000 пар точек) предъявляет высокие требования к производительности средств обработки и увеличивает время расчетов. В связи с этим часто применяют аппроксимацию этой характеристики выражениями, описывающими каждый участок ДХН. Метод кусочной аппроксимации заключается в замене участков 0–1, 1–2, 2–3, 3–4, 4–5, 5–6 ДХН аппроксимирующими кривыми, описываемыми полиномами вида
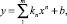
где kn – коэффициенты, описывающие наклон и изгибы кривой; b – коэффициент, описывающий смешение кривой относительно оси абцисс; m – максимальная степень полинома.
Такая замена ДХН позволяет вести расчет аналитически с помощью линейных уравнений, а в случае необходимости определять требуемое количество точек ДХН.
Типы дефектов в исследуемых пропорциональных электромагнитах
|
Номер ДХН |
Вид технологического отступления от номинала |
Максимальное значение магнитного потока, Вб |
|
1 |
Без технологических отступлений |
0,147 |
|
2 |
На 10 % от номинала уменьшено количество витков рабочей обмотки |
0,129 |
|
3 |
На 10 % от номинала увеличено количество витков рабочей обмотки |
0,166 |
|
4 |
На 10 % от номинала уменьшена индукция насыщения магнитного материала якоря |
0,136 |
|
5 |
На 10 % от номинала увеличена индукция насыщения магнитного материала якоря |
0,158 |
|
6 |
На 10 % от номинала уменьшена индукция насыщения магнитного материала ярма |
0,146 |
|
7 |
На 10 % от номинала увеличена индукция насыщения магнитного материала ярма |
0,148 |
|
8 |
На 10 % от номинала уменьшена индукция насыщения магнитного материала корпуса |
0,146 |
|
9 |
На 10 % от номинала увеличена индукция насыщения магнитного материала корпуса |
0,148 |
Проведена аппроксимация ДХН, измеренных с помощью прибора MagHyst [9] для ряда пропорциональных электромагнитов. При этом взяты характеристики как кондиционных устройств (ДХН1), так и электромагнитов с различными технологическими отступлениями (ДХН2 - ДХН9) (таблица).
Для наглядности далее будем рассматривать только восходящую ветвь ДХН, т.е. участки 0–1, 1–2, 2–3.
Из-за неоднозначности ДХН (при одном значении тока характеристика может принимать несколько значений магнитного потока), рассмотрим не зависимость Ф(i) (рис. 2), а обратную характеристику i(Ф) (рис. 3).
Первый и второй участки ДХН можно описать полиномом первой степени. Первый выходит из начала координат по этому коэффициент b(1) = 0:
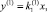
второй участок ДХН имеет вид
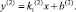
Третий участок можно описать полиномом второй или третьей степени:
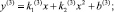
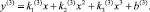
На рис. 4 приведена ДХН 1, с аппроксимациями третьего участка второй и третьей степенью.
Погрешность при применении полинома второй степени составила 8 %, а при применении полинома третьей степени не превысила приемлемые для магнитных измерений 3 %. Для определения погрешности аппроксимации находят различия между исходной и аппроксимирующей характеристиками. Метод нахождения погрешности аппроксимации [1, 5, 6] поясняет рис. 5. На исходной Ф1(I) задаются рядом точек, в которых строят перпендикуляры до пересечения с аппроксимирующей характеристикой Ф2(I).
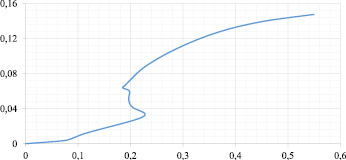
Рис. 2. ДХН вида Ф(i) кондиционного пропорционального электромагнита
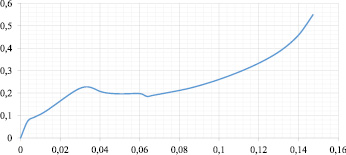
Рис. 3. ДХН вида i(Ф) кондиционного пропорционального электромагнита
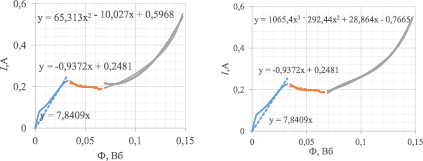
Рис. 4. Аппроксимированная ДХН 1 вида i(Ф)
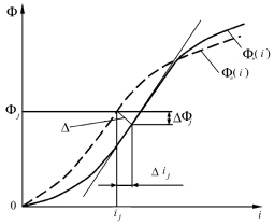
Рис. 5. Метод нахождения погрешности аппроксимации
Абсолютные погрешности по магнитному потоку Ф и току I в каждой исследуемой точке определяют как проекции отрезков заключенных между образцовой и измеренной характеристиками ΔФ и ΔI на оси координат. Относительные погрешности по току I и потоку Ф, а также полная погрешность измерения характеристики определяются выражениями
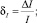
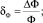
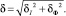
Из полученных результатов выбирается максимальный и принимается в качестве погрешности аппроксимации.
На рис. 6 представлены ДХН2 - ДХН9 пропорциональных электромагнитов с различными технологическими отступлениями от номинала.
В результате исследований можно сделать вывод о целесообразности применения аппроксимирующих выражений для описания динамических характеристик намагничивания. Применение данного подхода позволит сократить объем измерительной информации без ее потери, что положительно скажется на скорости обработки данных. Например, для описания каждой из исследуемых характеристик использовался массив из 15000 пар точек, а после применения аппроксимации требуется семь значений коэффициентов аппроксимирующих полиномов и четыре значения, задающие точки соединения участков 0–1, 1–2, 2–3.
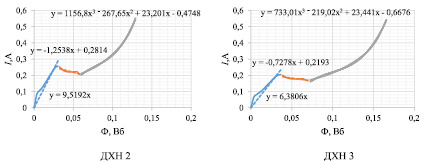
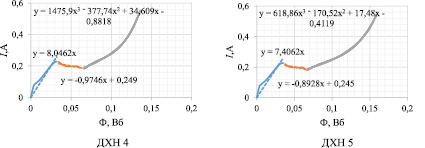
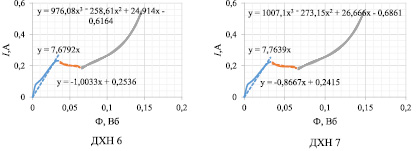
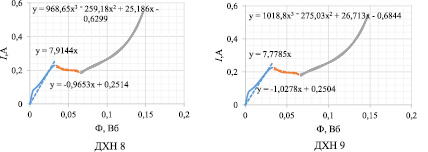
Рис. 6. ДХН пропорциональных электромагнитов с технологическими отступлениями от номинала
Результаты работы получены при поддержке гранта РФФИ № 15-38-20652 «Развитие теории бессенсорных прогнозирующих методов управления и диагностики электроприводов» с использованием оборудования ЦКП «Диагностика и энергоэффективное электрооборудование» ЮРГПУ (НПИ).



