В большинстве случаев расписание множества независимых друг от друга векторов действий является транспортным расписанием [1]. «Одним из представителей транспортных систем с достаточно жесткими ограничениями является железнодорожный транспорт с постоянным сезонным расписанием пассажирских поездов» [4]. Задача формирования расписания поездов в европейских публикациях рассматривается в двух видах: цикличном [9] и нецикличном [7].
Цикличные расписания характерны для западноевропейских стран с высокой плотностью населения и большими пассажиропотоками. Цикличные расписания обеспечивают строгую периодичность в пределах суток или части суток. В российских условиях при значительных расстояниях между крупными городами цикличные расписания пассажирских перевозок пока не применимы.
К нецикличным расписаниям относят расписания пассажирских поездов дальнего следования и расписания грузовых поездов. Большинство моделей формирования нецикличных расписаний основаны на процедурах линейного программирования и приводят к задачам большой размерности, для решения которых используют эвристики, такие как релаксация по Лагранжу [8], генерация колонок [6], задача цеха [5].
В процессе алгоритмизации и разработки программного обеспечения для формирования расписаний использованы следующие концепции [1]: программное решение задачи в рамках СУБД; двухэтапный процесс решения; идеология жадного алгоритма; концепции загруженности и равномерности; использование методов ранжирования.
Двухэтапный процесс решения задачи включает формирование начального расписания и последующую его оптимизацию. Под начальным расписанием понимается программно сформированное расписание при соблюдении обязательных ограничений.
Целью статьи является представление эвристических методов формирования начального расписания движения пассажирского железнодорожного транспорта дальнего следования.
Для расписаний пунктов остановок и перегонов использованы представления (рис. 1), в которых спираль является осью времени с отсчетом от ее начала, а длина спирали соответствует интервалу расписания [3]. Виток спирали – наименьший период расписания. Пометками на спирали фиксируется прибытие/отправление транспортного средства.
Задача формирования начального расписания решается последовательным выбором очередного маршрута и последующим его включением в расписание в определяемое время отправления с начальной станции. Выбор маршрута базируется на концепции загруженности, то есть на каждом шаге определяется наиболее загруженный по требуемым ресурсам маршрут. Выбор времени включения этого маршрута базируется на концепции равномерности использования ресурсов системы. То есть на каждом шаге формирования начального расписания присутствуют две операции выбора.
Такой подход характерен для жадных алгоритмов и применим для задач формирования расписаний и связанных с этим задач распределения ресурсов. Использование идеологии жадных алгоритмов требует цикличности процедур задачи формирования расписания.
Операции выбора в представляемых алгоритмах являются многокритериальными и для их реализации привлечен аппарат методов ранжирования [2].
Введем необходимые в математическом моделировании расписания обозначения.
Исходные данные задачи:
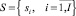 – множество станций железнодорожной сети;
– множество станций железнодорожной сети;
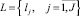 – множество перегонов железнодорожной сети;
– множество перегонов железнодорожной сети;
pli – количество платформ для высадки/посадки пассажиров i-ой станции;
Δti,j – минимальный интервал времени между двумя последующими поездами при выезде/въезде с j-го перегона на i-ю станцию;
F = {(s, l), s ∈ S, l ∈ L} – множество инцидентных пар – станция s является одной из двух граничных станций перегона l. Количество элементов множества F составляет nf = 2•J;
nr – количество маршрутов железнодорожной сети;
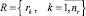 – множество векторов заявок маршрутов;
– множество векторов заявок маршрутов;
nk,s – количество станций маршрута rk;
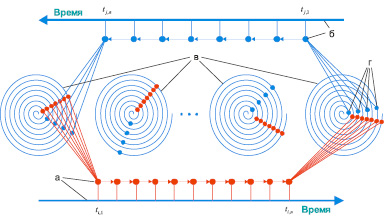
Рис. 1. Схема расписаний для векторов заявок: а – расписание (вектор) i-го маршрута; б – расписание (вектор) j-го маршрута: в – спиральные представления расписаний пунктов остановок; г – события периодов расписания пункта остановки
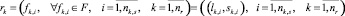 (1)
(1)
– вектор заявок маршрута; rk – последовательность пар – перегон/станция от начальной станции до конечной;
nd – количество суток интервала расписания;
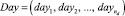 – упорядоченный во времени вектор суток;
– упорядоченный во времени вектор суток;
Interval = 24•nd – интервал расписания, часы;
nk – количество суток отправления поездов k-го маршрута;
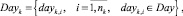
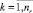 – множество суток отправления поездов маршрутов;
– множество суток отправления поездов маршрутов;
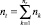 – количество поездов расписания;
– количество поездов расписания;
 – множество инцидентных пар, частично формирующих заявки поездов маршрутов – поезд маршрута r отправляется с начальной станции в день day;
– множество инцидентных пар, частично формирующих заявки поездов маршрутов – поезд маршрута r отправляется с начальной станции в день day;
используя (1), получаем множество заявок поездов маршрутов:
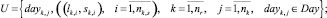 (2)
(2)
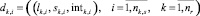 – заявка на прохождение маршрута k по i-му перегону на i-ую станцию, где intk,i – интервал времени движения от i – 1-й до i-й станции;
– заявка на прохождение маршрута k по i-му перегону на i-ую станцию, где intk,i – интервал времени движения от i – 1-й до i-й станции;
заявка на прохождение поезда uk,i по i-му перегону на i-ую станцию
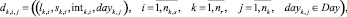 (3)
(3)
где dayk,j принимается равным дню отправления поезда маршрута.
Исходные расчетные данные задачи:
nti, 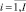 – количество поездов, проходящих через i-ую станцию;
– количество поездов, проходящих через i-ую станцию;
nlj, 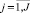 – количество поездов, проходящих через j-й перегон.
– количество поездов, проходящих через j-й перегон.
Переменные задачи:
ni – количество включенных в начальное расписание маршрутов;
nr – количество не включенных в начальное расписание маршрутов;
nit – количество включенных в начальное расписание поездов;
niti – количество поездов начального расписания, проходящих через i-ую станцию;
nilj – количество поездов начального расписания, проходящих через j-й перегон;
ti, tf – время прибытия/отправления поездов на станцию;
til, tfl – время выезда поездов на перегон и с перегона;
TIk – время отправления поездов маршрута rk с начальной станции, TIk = tik,1;
событие расписания, порождаемое заявкой (3), по прохождению поезда uk,j маршрута rk по i-му перегону на i-ую станцию будет определяться следующим выражением:
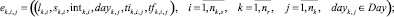 (4)
(4)
dayk,j; tik,i,j и tfk,i,j в (4) определяются на каждом шаге формирования расписания;
оценка загруженности i-й станции по проходящим через нее поездам
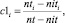
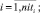 (5)
(5)
оценка загруженности j-го перегона по проходящим через него поездам
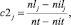
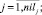 (6)
(6)
скалярная оценка загруженности k-го маршрута по суткам расписания
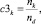
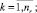 (7)
(7)
оценка равномерности события расписания i-й станции k1k,i,j
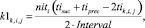
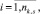
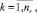
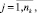 (8)
(8)
где tiprec и tisuc – времена прибытия на i-ую станцию поездов, предшествующих и последующих по отношению ко времени tik,i,j в интервале расписания (рис. 2);
оценка равномерности распределения события ek,i,j в периодах расписания i-й станции
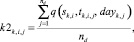 (9)
(9)
где
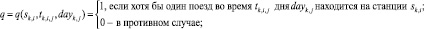
q ∈ Qs – множество булевых обозначений событий станций;
оценка равномерности события расписания i-го перегона k3k,i,j
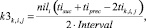
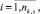
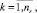
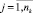 (10)
(10)
где tiprec и tisuc – времена начала движения поездов на i-м перегоне, предшествующие и последующие по отношению ко времени tik,i,j;
оценка равномерности распределения события ek,i,j в периодах расписания i-го перегона на въезде/выезде со станции
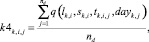 (11)
(11)
где

q ∈ Ql – множество булевых обозначений событий перегона.
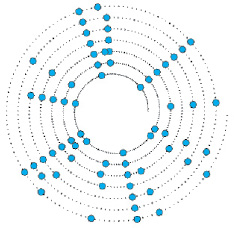
Рис. 2. Расписание событий расписания i-й станции/i-го перегона (въезд/выезд)
Задача формирования начального расписания состоит в цикличном выборе очередного маршрута rni+1 и формировании расписания 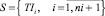 , которое минимизирует векторы оценок равномерности событий станций и перегонов выбранного маршрута
, которое минимизирует векторы оценок равномерности событий станций и перегонов выбранного маршрута
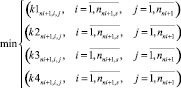 (12)
(12)
при обязательных ограничениях
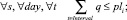 (13)
(13)
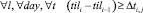
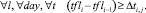 (14)
(14)
Целевая функция (12) обеспечивает многокритериальную минимизацию оценок равномерности. Ограничения (13) предотвращают одновременное нахождение поездов на станции более количества путей с пассажирскими платформами. Ограничения (14) отражают соблюдение интервала между последовательными выездами/въездами поездов.
Оценки загруженности станций (5) и перегонов (6) формируют множества первых и вторых векторных компонент загруженности маршрутов
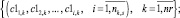 (15)
(15)
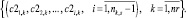 (16)
(16)
Многокритериальное ранжирование векторов (15) и (16) порождает множества рангов маршрутов по загруженности станций и перегонов
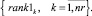 (17)
(17)
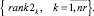 (18)
(18)
Обратная сортировка выражений (7) порождает множество рангов маршрутов по загруженности суток интервала расписания:
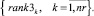 (19)
(19)
Ранги (17), (18), (19) формируют множество векторов маршрутов:
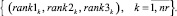 (20)
(20)
Старший по рангу маршрут, полученный многокритериальным ранжированием векторов (20), является самым загруженным и становится очередным кандидатом rni+1 на включение в начальное расписание.
Для определения времени отправления с начальной станции TIni+1 поездов маршрута rni+1 циклично выполняются следующие действия:
для tini+1,1 = 0 с шагом = 0,1 ч до 24 ч определение значений оценок (8)–(11) для перегонов и станций маршрута с накоплением множеств векторов с учетом ограничений (13), (14)
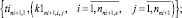 (21)
(21)
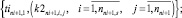 (22)
(22)
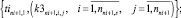 (23)
(23)
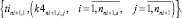 (24)
(24)
Многокритериальные ранжирования векторов (21), (22), (23), (24) формируют множества векторов рангов для начальных времен движения поездов маршрута rni+1
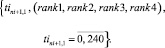 (25)
(25)
Многокритериальное ранжирование векторов (25) определяет начальное время TIni+1 движения поездов маршрута rni+1 в начальном расписании.
Для проверки корректности предлагаемых решений было разработано тестовое задание для пассажирского железнодорожного транспорта. Структура железнодорожной сети тестового задания (рис. 3) содержит сетевидные, паутинообразные и магистральные фрагменты сети. Нумерация станций и перегонов осуществлена случайным образом, поэтому можно положить эти номера их идентификаторами в базе данных. Тестовое задание имеет следующие характеристики: количество станций – 100; количество перегонов – 128; общее количество маршрутов – 100; количество поездов маршрутов – 471 в неделю.
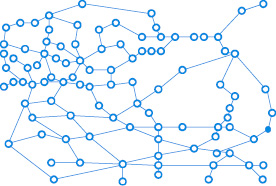
Рис. 3. Железнодорожная сеть тестового задания
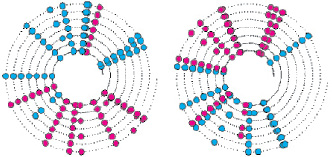
Рис. 4. Расписания въезда/выезда с перегона на граничные станции:  – выезд на перегон;
– выезд на перегон;  – въезд на станцию
– въезд на станцию
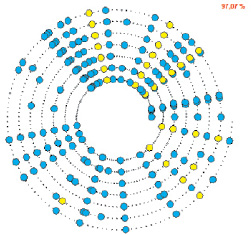
Рис. 5. Расписание въезда поездов на станцию:  – с одного перегона ;
– с одного перегона ;  – двух поездов с разных перегонов
– двух поездов с разных перегонов
На рис. 4 и 5 представлены визуализированные результаты формирования начального расписания железнодорожной сети для самых загруженных перегона и станции.
На рис. 5 в верхнем правом углу указано среднеквадратичное отклонение интервала между событиями станции от среднего значения в процентах.
Заключение
Авторы считают, что в данной работе новыми являются следующие положения и результаты:
осуществлена формализация задачи формирования транспортного расписания;
представлены общие подходы и алгоритмы решения задач формирования железнодорожных расписаний пассажирских поездов дальнего следования с использованием методов ранжирования теории принятия решений.



