Автоматизация поиска цифровой информации является необходимостью, обусловленной большим количеством информации в электронном (оцифрованном) виде. С ростом объемов электронных библиотек, полнотекстовых баз данных, фондов информации различного вида возникает проблема ускорения поиска информации [9, 10]. В качестве алгоритмической основы разработки быстродействующих систем поиска можно рассматривать разрядное распараллеливание операций сравнения слов и элементов строкового типа. С этой целью ниже излагается метод поразрядно-параллельного сравнения чисел и данных строкового типа. Метод возникает в результате переноса на рассматриваемый случай поразрядно-параллельного алгебраического сложения чисел, который не включает операций вычисления переноса. Целью переноса является разработка основы для максимально параллельного выполнения базовых операций поиска, включая сравнение, сортировку и распространение метода одновременно на поиск чисел и строк.
В рамках данной задачи требуется выполнять поразрядно-параллельную идентификацию знака старшего ненулевого разряда в знакоразрядном коде. Для этой цели синтезируется алгоритм, который может быть реализован как программно, так и аппаратно, при этом требуется такое его представление, которое допускало бы обобщение в аспекте поразрядно-параллельной обработки слов. Обобщение строится как способ параллельной идентификации всех совпадающих частей сравниваемых слов.
Метод поразрядно-параллельного алгебраического сложения заимствуется из [1, 2]. Пусть два двоичных полинома
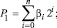
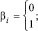
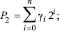
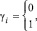(1)
условно расположены в двух входных разрядных сетках (РС),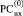 
и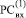 
, номера клеток которых совпадают с индексами коэффициентов из (1).
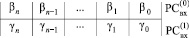(2)
Синхронно и взаимно независимо по всем номерам разрядов j из (2) выполняется операция βj + γj суммирования двоичных коэффициентов равного веса по вертикали (CBj). Результат CBj представляется в двоичном коде
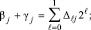
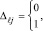j = 0, 1, ..., n. (3)
Коэффициенты из (3) располагаются по диагонали двух выходных РС, –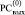 
и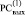 
, образуя диагональную от j-го разряда запись (Дj – запись) вида
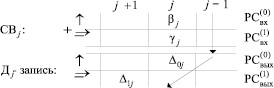. (4)
Предварительный результат сложения:
, (5)
где Δj = Δ0j; ∇j = Δ1(j–1) из (4), j = 0, 1, ..., n, n + 1.
Все переносы в (5) оказываются взаимно отделенными вертикальными парами нулей [2]:
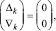k = const,
где Δk, ∇k из (5), 0 ≤ k ≤ n + 1, поскольку при любом j из (4) складываются не более двух единиц одинакового веса. Аналогично, в (4) по диагонали Дj-записи от 1 в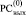 
не может располагаться 1 в 
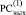. На этой основе корректным является следующее преобразование промежуточного набора (5) [2]. Все разряды, имеющие значение Δj ≠ 0, из 
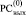(и только из 
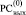) в (5) подвергаются тождественному преобразованию:
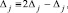j = 0, 1, ..., n. (6)
При этом правая часть (6) размещается в j-й клетке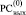 
и в (j + 1)-й клетке 
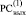в порядке Дj-записи для всех номеров j преобразуемых разрядов:
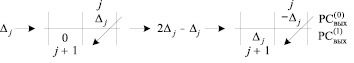. (7)
Преобразование (7) корректно, поскольку в (j + 1)-й клетке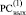 
всегда находится ноль – до применения (6) – при условии, что в 
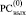Δj ≠ 0, иначе Дj-запись означала бы результат сложения трех единиц веса j-го разряда, тогда как их число не больше двух [1, 2].
Вслед за тем параллельно по всем j = 0, 1, ..., n, n + 1 выполняется шаг вертикального сложения, результатом которого в каждом разряде всегда будет либо 0, либо +1, либо –1 [1, 2]. При этом значение знакоразрядного кода расположится в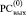 
, где, таким образом, сформируется окончательное значение вычисляемой суммы P1 и P2 из (1).
Временная сложность T параллельного сложения в знакоразрядном коде составит ≈ 2τ при количестве элементов Sl сумматора пропорциональном числу разрядов слагаемых:
T ≈ 2τ = O(1); Sl ≈ 4(n +1) = O(n).
Сравнение двоичных чисел
Предполагается, что сравниваемые числа имеют формат (1) с нумерацией разрядов справа налево. Пусть число A принимается за уменьшаемое, B – за вычитаемое, тогда B записывается в обратном коде (единицы заменяются нулями, нули – единицами), затем используется тождественное преобразование [2]:
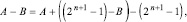(8)
с учетом
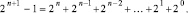(9)
или, в позиционной системе,
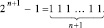(10)
Над числом A и числом B, взятым в обратном коде, параллельно по всем номерам разрядов выполняется операция CBj, затем A и B (в обратном коде) суммируются по схеме (2)–(7). Для восстановления правильного результата вычитания учитывается (8)–(10): от однорядного знакоразрядного двоичного кода полученного результата следует вычесть 2n+1 – 1. Это равносильно тому, что с полученным результатом складывается –2n+1 + 1 – к младшему разряду добавляется +1, а к разряду веса 2n+1 добавляется –1.
Знак сравнения A и B определяется знаком старшего ненулевого разряда однорядного знакоразрядного двоичного числа, полученного в скорректированном окончательном результате. Если знак этого разряда отрицательный, то A < B, если положительный, то A > B, если все разряды нулевые, то A = B.
Разрядное распараллеливание сравнения строк
Метод переносится [5] на сравнение элементов строкового типа, для краткости – строк. Все символы представляются в ASCII-коде в двоичной форме. Набор двоичных кодов всех символов строки в порядке расположения интерпретируется как единое числовое значение. Сравнение полученных двоичных кодов выполняется путем алгебраического сложения, изложенным поразрядно-параллельным способом, однако при этом, в соответствии с лексикографическим упорядочением слов, выравнивание весов разрядов выполняется по старшим разрядам, недостающие младшие разряды дополняются нулями. Например, сравниваются слова ‘poisk’ и ‘primer’. Их двоичный код с выравниваем старших разрядов соответственно примет вид
0 1 1 1 0 0 0 0 0 1 1 0 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 1 0 0 1 1 0 1 1 0 1 0 1 1 0 0 0 0 0 0 0 0
0 1 1 1 0 0 0 0 0 1 1 1 0 0 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 1 0 1 0 1 1 0 0 1 0 1 0 1 1 1 0 0 1 0
Слово «poisk» интерпретируется как уменьшаемое, «primer» – как вычитаемое. После перевода вычитаемого в обратный код алгебраическому сложению подлежат
0 1 1 1 0 0 0 0 0 1 1 0 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 1 0 0 1 1 0 1 1 0 1 0 1 1 0 0 0 0 0 0 0 0
1 0 0 0 1 1 1 1 1 0 0 0 1 1 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 0 1 0 1 0 0 1 1 0 1 0 1 0 0 0 1 1 0 1
Параллельно по всем номерам разрядов выполняется операция CBj:
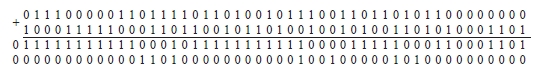
Согласно (5)–(7) выполняется преобразование:
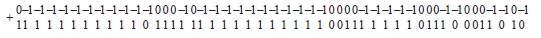
Параллельное по всем разрядам суммирование по вертикали влечет
1 0 0 0 0 0 0 0 0 0 0 –1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 –1 0 0 1 0 –1 1 –1
Результат корректируется в соответствии с (8)–(11), что влечет окончательное значение алгебраической суммы
0 0 0 0 0 0 0 0 0 0 0 –1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 –1 0 0 1 0 –1 1 0
Старший ненулевой разряд отрицателен, следовательно, первое слово лексикографически меньше второго: ‘poisk’ < ‘primer’.
Численное и программное моделирование способа представлено в [3, 4].
Без учета временной сложности идентификации старшего ненулевого разряда изложенное сравнение независимо от числа разрядов занимает время одной бинарной операции над двоичными коэффициентами одного веса –
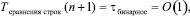
где n + 1 – число разрядов двоичного представления строки.
Алгоритм идентификации знака старшего ненулевого разряда
Поразрядно-параллельное нахождение старшего ненулевого разряда в знакоразрядном коде – самостоятельная схемотехническая задача. Такой разряд можно выделить программно или аппаратно, например, при помощи схемы, представленной в [8]. Можно, с другой стороны, выделить старший ненулевой разряд аналогично нормализации мантиссы числа с плавающей точкой с помощью параллельного сдвигателя, описанного в [2].
Ниже для выполнения идентификации знака старшего ненулевого разряда предлагается использовать схему сдваивания для всей последовательности n + 1 разрядов следующего вида.
Сдваивание начинается от старшего разряда (рис. 1)
На рис. 1 под операцией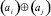 
(аналогично, 
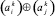) понимается следующий способ выбора и сохранения знака в зависимости от знака операндов: если ai ≠ 0, то выбирается и сохраняется знак ai, причем независимо от знака и значения aj; если ai = 0 и aj ≠ 0, то выбирается и сохраняется знак aj; если ai = 0 и aj = 0, то в качестве значения 
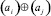(аналогично, 
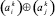) выбирается и сохраняется значение 0.
Ниже дана формализация алгоритма идентификации знака старшего ненулевого разряда на основе схемы сдваивания с представленной выше интерпретацией операции в узлах схемы.
Алгоритм 1
Шаг 1. Если старший разряд an ≠ 0, то по его значению идентифицируется знак старшего разряда и результат сравнения, иначе положить j = 1,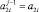 
, 
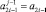и перейти на шаг 2.
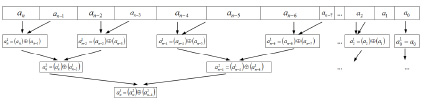
Рис 1. Схема сдваивания для идентификации знака старшего ненулевого разряда
Шаг 2. По схеме сдваивания на вход узла текущего уровня поступают значения разрядов. Для каждой пары с номером i (нумерация от нуля справа налево) происходит передача значения на следующий уровень по правилу:
2.1. Если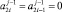 
, на уровень с номером j передается значение 0.
2.2. Если один из элементов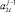 
или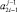 
имеет нулевое значение, а другой элемент – ненулевое значение, то на уровень с номером j передается значение ненулевого элемента.
2.3. Если элементы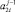 
или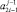 
имеют ненулевое значение, то на уровень с номером j передается значение старшего в паре ненулевого элемента 
.
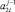Перейти на шаг 3.
Шаг 3. Если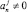 
, то по его значению идентифицируется знак старшего разряда и результат сравнения, выполнить переход на шаг 4, или, если 
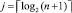, то выполнить переход на шаг 4. Иначе положить j = j + 1 и выполнить переход на шаг 2.
Шаг 4. Конец. Алгоритм заканчивает работу по следующему условию: крайняя слева ветвь (путь значения старшего разряда) при сдваивании встречает в узле ненулевое значение (пример 1, 2), или на шаге с номером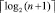 
в узле этой ветви (в корне двоичного дерева, пример 3) оказывается разряд с нулевым значением.
Иными словами, отслеживание знака старшего ненулевого разряда выполняется по шагам пути старшего разряда схемы сдваивания (левые узлы схемы сдваивания) до первого уровня с ненулевым значением узла, которое и явится идентификатором знака (пример 1). Если ненулевое значение не появилось, то на шаге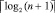 
алгоритм останавливает свою работу, идентифицируя совпадение слов (равенство двоичных кодов).
Пример 1. Сравнить слова ‘Anna’ и ‘Alla’.
Двоичный код сравниваемых слов с выравниванием старших разрядов соответственно примет вид
0 1 0 0 0 0 0 1 0 1 1 0 1 1 1 0 0 1 1 0 1 1 1 0 0 1 1 0 0 0 0 1
0 1 0 0 0 0 0 1 0 1 1 0 1 1 0 0 0 1 1 0 1 1 0 0 0 1 1 0 0 0 0 1
Применяя схему, описанную в п. II, получаем
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0
Знак старшего ненулевого разряда определяется по алгоритму 1 на рис. 2.
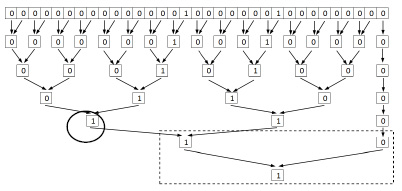
Рис. 2. Пример идентификации знака старшего ненулевого разряда
Временная сложность схемы идентификации знака старшего ненулевого разряда определяется числом уровней двоичного дерева, которое не больше логарифма от числа двоичных разрядов строки, поэтому
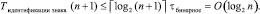(11)
Способ поразрядно-параллельной идентификации всех совпадающих фрагментов двух строк
Аналог изложенного способа идентификации старшего ненулевого разряда можно распространить на поразрядно-параллельную идентификацию всех совпадающих фрагментов двух строк. Главная особенность в отличие от прототипа состоит в том, что выполняется только один – первый – шаг поразрядно-параллельного вертикального сложения CBj двоичных кодов двух сравниваемых строк.
Очевидно, что все совпадающие по номерам разрядов биты в результате первого шага поразрядно-параллельного вертикального сложения CBj двоичных кодов сравниваемых слов дадут в верхней разрядной сетке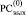 
нули: согласно (4) Δ0j = 0 тогда и только тогда, когда либо βj = 0 ∧ γj = 0, либо βj = 1 ∧ γj = 1.
Замечание 1. Нетрудно видеть, что в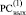 
при этом Δ1j = 0, если βj = 0 ∧ γj = 0, и Δ1j = 1, если βj = 1 ∧ γj = 1, хотя непосредственно ниже сам этот факт нигде не будет использоваться.
Количество таких нулей, идентифицирующих в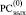 
совпавшие фрагменты, равно числу бит двоичного представления каждого из пары совпавших фрагментов, а расположение этих нулей соответствует весам разрядов их двоичного представления.
Каждая в отдельности группа подряд идущих нулей (совпадающих бит) может быть идентифицирована по аналогии с алгоритмом 1 для выделения старшего ненулевого разряда (рис. 2). Именно идентификация цепочки подряд идущих нулей в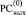 
будет начинаться с первого слева направо нуля после каждого единичного бита, схема сдваивания будет заканчиваться первым слева направо единичным (см. замечание 2) битом после нуля вдоль пути исходного (первого слева направо) нуля по шагам схемы сдваивания.
Замечание 2. Слева от старшего разряда всегда формально полагается еще один единичный разряд за границей разрядной сетки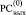 
для правильного формального начала алгоритма – справа от единицы. С целью правильного формального окончания алгоритма первым слева направо единичным значением за границей разрядной сетки 
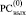справа формально дописывается еще один единичный разряд.
Данный аналог алгоритма 1 поясняется на следующем примере.
Пример 2. Идентифицировать все совпадающие части в словах ‘Май’ и ‘Мой’.
Двоичный код сравниваемых слов с выравниванием старших разрядов соответственно примет вид
1 1 0 0 1 1 0 0 1 1 1 0 0 0 0 0 1 1 1 0 1 0 0 1
1 1 0 0 1 1 0 0 1 1 1 0 1 1 1 0 1 1 1 0 1 0 0 1
Поразрядно-параллельное сложение (3)–(5) влечет
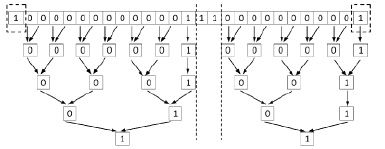
Рис. 3. Пример идентификации групп подряд идущих нулей в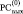 
Для идентификации группы подряд идущих нулей в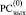 
применяется рассматриваемый аналог алгоритма 1 (рис. 3).
Согласно замечанию 2 слева от старшего разряда за границей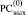 
всегда формально полагается еще один единичный разряд (пунктир слева на рис. 3), за границей справа также формально полагается еще один единичный разряд (пунктир справа на рис. 3).
Идентификацию совпадающих частей формализует следующий алгоритм.
Алгоритм 2
Шаг 1. Слева от старшего разряда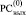 
всегда формально полагается еще один единичный разряд для правильного формального начала алгоритма справа от единицы. Перейти на шаг 2.
Шаг 2. За границей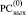 
справа формально дописывается еще один единичный разряд (пунктир справа на рис. 3) – для правильного формального окончания алгоритма. Перейти на шаг 3.
Шаг 3. Идентификация каждой группы начинается с первого слева направо нуля, после ненулевого бита. При этом идентификация первого слева направо от цепочки нулей единичного бита выполняется по алгоритму 1. Перейти на шаг 4.
4. Если идентифицирован единичный разряд за границей разрядной сетки (справа), то идентификация совпадающих частей завершена (единица в идентифицированное совпадение не входит), иначе перейти на шаг 3.
Число нулей идентифицированной группы равно числу бит двоичного представления совпавших фрагментов. Это число, равно как и местоположение идентифицированных промежуточных нулей, определяется весами (номерами) начального и конечного единичного разрядов в схеме сдваивания, выполняемой по алгоритму 2.
Анализ выполняется параллельно по всем группам подряд идущих нулей. При этом в каждой группе данный анализ выполняется по алгоритму 2 от соответственного анализируемой группе первого слева направо ненулевого разряда вдоль пути, который проходит значение соседнего справа нулевого разряда по схеме сдваивания сверху вниз к корню двоичного дерева. Алгоритм останавливает работу на том шаге вдоль этого пути, где в узле первый раз встретилось ненулевое значение. В анализ по алгоритму 2 необходимо включать все подряд младшие разряды справа от первого нулевого.
На рис. 4 обведенный кружочком узел идентифицирует старший ненулевой разряд, поэтому обведенную пунктиром часть схемы выполнять уже излишне.
Параллелизм заключается в синхронной работе по алгоритму 2 одновременно от каждого первого слева направо нулевого разряда соответственной группы. Так вторая группа нулей идентифицируется одновременно с первой (рис. 5).
Рис. 3 является условным, полную и правильную иллюстрацию способа дает его декомпозиция на рис. 4, 5.
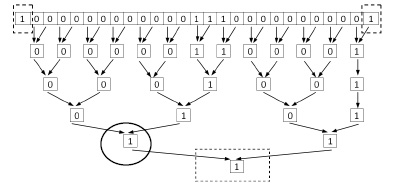
Рис. 4. Идентификация первой слева направо группы подряд идущих нулей по алгоритму 2
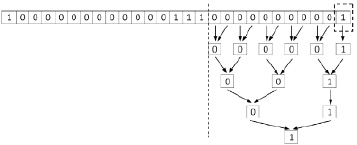
Рис. 5. Идентификация второй слева направо группы подряд идущих нулей по алгоритму 2
Временная сложность схемы параллельной идентификации всех групп подряд идущих нулей по алгоритму 2 в двоичном представлении любой строки (любого элемента строкового типа) определяется числом уровней двоичного дерева, которое не больше логарифма от числа нулевых двоичных разрядов группы, а также количеством таких параллельно обрабатываемых деревьев. В результате
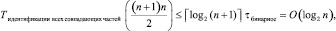(12)
где по-прежнему n + 1 – число разрядов двоичного представления строки, выражение в скобках левой части неравенства – количество процессорных (логических) элементов.
Области применения
Предложенная схема позволяет выполнить поразрядно-параллельный поиск в строке одновременно по нескольким маскам, параллельно идентифицировать полное и частичное совпадение с одной или несколькими масками поиска с временной сложностью (12). Схема распространяется на выявление совпадающих частей любой информации в двоичном коде, включая числовую. Без принципиальных изменений схема переносится на параллельную идентификацию значений условных выражений. С применением максимально параллельной сортировки [6, 7] схема применима для ускорения операций поиска, вставки, замены в двоичных и декартовых деревьях структуры баз данных. Кроме того, схема может быть применена к идентификации бинарных двоично закодированных изображений или их фрагментов. Для этого достаточно матрицу изображения перевести в одномерный массив. Аналогично, могут идентифицироваться графы в матричном представлении. Схема позволяет идентифицировать участки несовпадения (совпадения) с эталоном, что целесообразно при идентификации биометрических данных.
Заключение
Изложен метод разрядного распараллеливания операций сравнения для информационного поиска. Метод основан на бинарном алгебраическом сложении полноразрядных чисел без вычислений переноса. Представлено видоизменение метода для параллельной идентификации совпадающих фрагментов строк с логарифмической временной сложностью. Одно из возможных применений заключается в ускорении операций поиска, вставки, замены в двоичных и декартовых деревьях структур баз данных. Возможно также применение для идентификации бинарных изображений и их фрагментов.