Особенностью сложных производственных систем является многостадийный процесс превращения сырья и исходных материалов в готовую продукцию. Каждый этап обработки накладывает свой отпечаток на регламентируемые стандартом показатели качества и определяет экономическую эффективность производства [10–14].
Одним из основных путей повышения эффективности работы таких производств являются разработка современных методов моделирования и создание соответствующего математического, алгоритмического и программного обеспечения. Важным является получение эффективных методов клеточно-иерархической идентификации и анализа сложных производств. Клеточно-иерархический подход основан на клеточной интерпретации и используется для описания сложных пространственно-распределенных производственных систем, характеризующихся многостадийностью обработки. Процесс обработки представляется в виде систем, образованных иерархией клеток, каждая из которых соответствует отдельному технологическому агрегату или стадии обработки. Описание в виде входов, состояний и выходов характеристик сырья, технологических параметров и свойств готовой продукции дает возможность моделировать технологии обработки любых видов продукции. Использование конечных, клеточных и вероятностных автоматов, итеративных цепей и сетей дает возможность описывать сложные пространственно-распределенные производственные системы. Подходы, основанные на формировании математических образов сложных промышленных систем, методы и алгоритмы обработки ретроспективной, текущей и экспертной информации о пространственно-распределенных объектах позволяют адекватно описывать сложные производственные системы. Отсутствие однозначных функциональных зависимостей между факторами технологии и свойствами готовой продукции, наличие случайных величин, влияющих на процесс обработки и показатели качества, привели к необходимости разработки методов оптимизации режимов функционирования сложных производственных систем и построению алгоритмов их реализации. Так как осуществляемые в них режимы обработки отличаются стохастическим характером протекающих процессов, разработаны методы моделирования, характеризующиеся учетом зависимости текущих состояний от всей предыстории.
Особенностью сложных пространственно-распределенных производственных систем является многостадийный процесс превращения сырья и исходных материалов в готовую продукцию. Каждый этап обработки накладывает свой отпечаток на регламентируемые стандартом показатели качества и определяет экономическую эффективность производства. Сложные системы, для которых принимаются решения, представляют собой совокупность взаимосвязанных объектов (стадий обработки, агрегатов, операций). Методология структурной клеточно-иерархической идентификации подходит для моделирования сложных пространственно-распределенных многостадийных промышленных объектов со стохастическим характером производства.
Для описания сложных промышленных объектов, базирующихся на клеточной интерпретации процессов, создается дерево технологических операций, формируются технологические цепочки с указанием необходимых агрегатов, определяются усредненные технологические режимы.
Использование сетей Петри позволяет моделировать сложную пространственно-распределенную производственную систему [1–9]. Процесс моделирования начинается с формирования функциональных блоков, соответствующих отдельным стадиям обработки. Задание информации при дискретном подходе сводится к заданию конечных множеств входов, состояний и выходов. Алфавиты входов, состояний и выходов могут иметь различную размерность. Сочетания алфавитов случайных величин формируют возможные позиции сети Петри.
При моделировании формируется сеть Петри, состоящая из нескольких «слоев», соответствующих этапам обработки. Этап состоит из нескольких переходов и позиций и отвечает за реализацию отдельного этапа.
Пример сети Петри, моделирующей процесс, состоящий из 4 стадий, приведен на рис. 1.
Отдельная стадия описывается двумя случайными величинами. Для простоты каждая величина имеет двоичный алфавит. В итоге на каждой стадии рассматриваются 4 сочетания алфавитов {(0,0), (0,1), (1,0), (1,1)}.
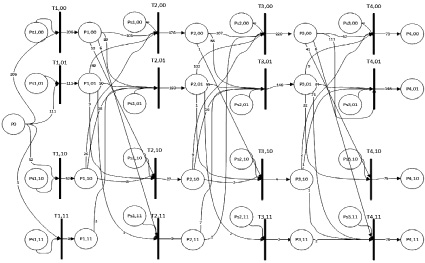
Рис. 1. Сеть Петри сложной пространственно-распределенной производственной системы
Отдельное сочетание алфавитов будет определять одну позицию, пометка в которой означает количество статистических данных, попавших в данный набор. Из указанной позиции исходят дуги в переходы к сочетаниям алфавитов следующего этапа производственного процесса. Для того, чтобы фишки из позиции перемещались только однократно через каждый переход, задается позиция-селектор Рsi.
Построим описанную сеть Петри. Обозначим:
– В первом слое:
- начальную позицию Р0.
- позиции-селекторы, определяющие распределение по наборам первого этапа Рs0,00, Рs0,01 Рs0,10, Рs0,11;
- переходы Т1,00, Т1,01, Т1,10, Т1,11.
– Во втором слое:
- входные позиции Р1,00, Р1,01, Р1,10, Р1,11;
- позиции-селекторы, определяющие распределение по наборам второго этапа Рs1,00, Рs1,01, Рs1,10, Рs1,11;
- переходы Т2,00, Т2,01, Т2,10, Т2,11.
– В третьем слое:
- входные позиции Р2,00, Р2,01 Р2,10, Р2,11;
- позиции-селекторы, определяющие распределение по наборам второго этапа Рs2,00, Рs2,01, Рs2,10, Рs2,11;
- переходы Т3,00, Т3,01, Т3,10, Т3,11.
– В четвертом слое:
- входные позиции Р3,00, Р3,01, Р3,10, Р3,11;
- позиции-селекторы, определяющие распределение по наборам второго этапа Рs3,00, Рs3,01, Рs3,10, Рs3,11;
- переходы Т4,00, Т4,01, Т4,10, Т4,11.
– Заключительные позиции, отвечающие за результаты работы многоэтапного процесса Р4,00, Р4,01, Р4,10, Р4,11.
Определим входные и выходные комплекты для переходов:
I(T1,00) = {Рs0,00, 206*Р0}; I(T1,01) = {Рs0,01, 111*Р0};
I(T1,10) = {Рs0,10, 52*Р0}; ; I(T1,11) = {Рs0,11, 3*Р0};
О(T1,00) = {206*Р1,00}; О(T1,01) = {111*Р1,01};
О(T1,10) = {52*Р1,10};;; О(T1,11) = {3*Р1,11};
I(T2,00) = {Рs1,00, 101*Р1,00, 89*Р1,01, 10*Р1,10, 6*Р1,11};
I(T2,01) = {Рs1,01, 49*Р1,00, 50*Р1,01, 9*Р1,10, 3*Р1,11};
I(T2,10) = {Рs1,10, 26*Р1,00, 18*Р1,01, 8*Р1,10, 0*Р1,11};
I(T2,11) = {Рs1,11, 0*Р1,00, 3*Р1,01, 0*Р1,10, 0*Р1,11};
О(T2,00) = {176*Р2,00}; О(T2,01) = {160*Р2,01};
О(T2,10) = {27*Р2,10}; О(T2,11) = {9*Р2,11};
I(T3,00) = {Рs2,00, 107*Р2,00, 68*Р2,01, 1*Р2,10, 0*Р2,11};
I(T3,01) = {Рs2,01, 102*Р2,00, 55*Р2,01, 1*Р2,10, 2*Р2,11};
I(T3,10) = {Рs2,10, 9*Р2,00, 16*Р2,01, 2*Р2,10, 0*Р2,11};
I(T3,11) = {Рs2,11, 2*Р2,00, 7*Р2,01, 0*Р2,10, 0*Р2,11};
О(T3,00) = {220*Р3,00}, О(T3,01) = {146*Р3,01};
О(T3,10) = {4*Р3,10}, О(T3,11) = {2*Р3,11};
I(T4,00) = {Рs3,00, 62*Р3,00, 111*Р3,01, 41*Р3,10, 6*Р3,11};
I(T4,01) = {Рs3,01, 9*Р3,00, 34*Р3,01, 32*Р3,10, 71*Р3,11};
I(T4,10) = {Рs3,10, 2*Р3,00, 1*Р3,01, 0*Р3,10, 1*Р3,11};
I(T4,11) = {Рs3,11, 0*Р3,00, 0*Р3,01, 2*Р3,10, 0*Р3,11};
О(T4,00) = {73*Р4,00}, О(T4,01) = {146*Р4,01};
О(T4,10) = {75*Р4,10}, О(T4,11) = {78*Р4,11}.
Здесь запись вида 73*Р4,00 означает, что в позицию Р4,00 осуществлено 73 перехода. Такие записи позволяют отразить частоты реализации переходов исследуемого процесса.
Рассмотрено 372 опыта. Начальная маркировка для рассматриваемой задачи будет: М(Р0) = 372,
М(Рs1,00) = М(Рs1,01) = М(Рs1,10) = М(Рs1,11) = = М(Рs2,00) = М(Рs2,01) = М(Рs3,10) = М(Рs3,11) = = М(Рs3,00) = М(Рs3,01) = М(Рs3,10) = М(Рs3,11) = 1,
для остальных позиций значение равно 0.
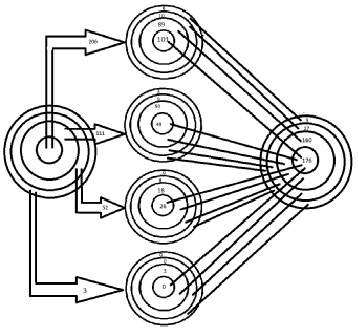
Рис. 2. Переходы первого слоя сети Петри
Пояснение переходов первого слоя сети Петри приведено на рис 2. В обобщённом виде переходы могут быть представлены в виде связи n-мерных шаров (где n – количество сочетаний алфавитов). Внутренний шар соответствует сочетанию (0,0), а внешний – сочетанию (1,1) (рис. 1).
Левый круг отражает возможные переходы изначальной позиции Р0, количество наблюдений в которых указано на исходящих стрелках. Средние четыре окружности отражают переходы из позиций первого слоя (этапа обработки) в позиции второго слоя. Правый круг показывает суммарные входы в позиции второго слоя.
Для моделирования сети Петри используется ее матричное представление. Матрица сети Петри размера m×n:
R = R+–R–,
где
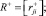
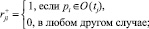
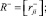
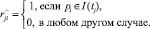
Выводы
Сети Петри позволяют моделировать параллельные процессы, протекающие в системе независимо один от другого. Параллельным процессам соответствуют состояния сетей Петри, описывающие отдельные стадии обработки в сложных производственных системах. Сети Петри позволяют наглядно отразить и смоделировать процессы, протекающие в таких системах.



