Известно, что математические понятия характеризуются высоким уровнем абстракции. В силу этого эффективное освоение, развитие и применение математических понятий учащимися может быть получено только в результате сложного, длительного, многоуровневого и многоэтапного учебного процесса. В таком процессе качественное освоение теоретической системы понятий возможно только при субъектности учащихся, их активной и напряженной познавательной деятельности. Однако, как показывает анализ школьной практики, существующая система обучения математике далеко не всегда обеспечивает подобную активность школьников. Часто имеет место низкое качество усвоения таких понятий, как «уравнение», «неравенство», «тождество», «функция», а также умений оперировать ими [5, с. 21].
Обновление школьного образования, направленное на формирование умений учащихся самостоятельно искать, извлекать и получать новые, необходимые знания, сталкивается с различными проблемами. Они связаны не только с несовершенством методик обучения, но и с механизмами, которые обеспечивают познавательную активность учащихся.
Многочисленные исследования констатируют, что система образования в целом не удовлетворяет современным требованиям и вследствие этого находится в состоянии кризиса. «Этот кризис развился на глазах практически одного поколения… О нем свидетельствуют: дальнейшее увеличение числа неграмотных в мире … разрастание такого сравнительно нового явления, как функциональная неграмотность… очевидные дисфункции систем образования, породившие повсеместное снижение его качества» [2, с. 3].
Во многом такое положение дел обязано тому, что по-прежнему в основной и старшей школе теоретические знания (и прежде всего, понятия) изучаются рядоположенно. При этом, как правило, используется индуктивно-эмпирическая схема обобщения [5]. Такой подход обычно подразумевает, что ученики должны понять материал, предложенный им в готовом виде. В результате не актуализируется и не поддерживается процесс формирования умений учащихся самостоятельно искать новые знания.
К тому же отметим, что в практике освоения математики не уделяется должное внимание развитию пространственного мышления – одного из видов образного мышления учащихся. Такое мышление формируется как специфический вид мыслительной деятельности, который необходим при решении разнообразных вопросов, связанных:
– с ориентацией в пространстве (и в реальном физическом пространстве, объекты которого нас окружают, и в воображаемом виртуальном пространстве);
– с анализом пространственных свойств и отношений реальных объектов, а также их представлений теми или иными пространственными образами (моделями);
– с мысленной трансформацией исходного пространственного образа, в том числе путем перегруппировки его составляющих, их наложением, совмещением, добавлением, усечением и т.п. [6].
Таким образом, актуален поиск новых образовательных средств, позволяющих учащимся активно овладевать базовыми понятиями и ведущими идеями математики, обеспечивая необходимое познание новых достижений науки и практики. При этом должны формироваться умения учащихся адекватно реагировать на новые ситуации, моделировать и прогнозировать результаты своей деятельности, делать аргументированные выводы.
В традиционной образовательной парадигме подразумевается, что учитель и учебник – это источники информации, предлагаемой к освоению, а учащиеся – это получатели и потребители этой информации. Такие роли эффективны только при высокой мотивации учащихся к учебной деятельности. Если же мотивация недостаточна, то возникает потребность в специальных методах ее «формирования» и «усиления». К ним относятся:
- обеспечение позитивной психологической атмосферы в классе, гуманные отношения учителя и учащихся, «принятие» учеников независимо от их учебных успехов и т.п.;
- личностно-ориентированный подход, при котором деятельность учителя ориентирована на личность учащегося, учитывает ее самобытность, самоценность, субъектный опыт;
- активные методы обучения, обеспечивающие инициативность учащихся, разнообразие их мыслительной и практической деятельности в процессе освоения учебного материала и т.д.
Принципиально новые возможности возникают в инновационной образовательной парадигме, целью которых является субъектное развитие учащихся, использование и обогащение ими собственного опыта, своих знаний и умений. В указанной парадигме учащиеся – это не столько получатели и потребители готовой учебной информации, сколько активные участники порождения и освоения такой информации. К тому же механизмы субъектности включают: оценку результатов и анализ условий, способствовавших достижению поставленных целей, а также накопление индивидуального опыта, фиксация результатов и способов своего саморазвития [4]. При этом обеспечиваются приоритеты математического образования – «развитие способностей:
- к логическому мышлению, коммуникации и взаимодействию на широком математическом материале (от геометрии до программирования);
- реальной математике: математическому моделированию (построению модели и интерпретации результатов), применению математики, в том числе с использованием ИКТ» [1, с. 5].
Отметим, что при системной реализации данной парадигмы формирование мотивации перестает быть отдельной и трудноразрешимой проблемой. Обновленная образовательная деятельность, в которой преобладает не традиционная учебная деятельность, а доминируют иные виды активности (производственно-учебная, исследовательско-учебная, проектно-учебная, имитационно-игровая и т.п.) становится для учащихся мощным фактором, естественно формирующим высокую мотивацию участия в ней, причем без использования дополнительных методов стимулирования.
Еще один существенный фактор усиления интереса учащихся заключается в полном и комплексном использовании возможностей зрительных каналов получения информации, которые способны «пропустить» в мозг почти в 5 раз больше информации, чем органы слуха, и почти в 13 раз больше, чем тактильные органы.
Что касается использования новых концептуальных подходов при освоении понятий школьной математики, то их можно обеспечить, используя дидактические возможности когнитивных динамичных компьютерных визуализаций. Известно, что для человека, воспринимающего зрительные образы, визуализация – это его мыследеятельность, направленная на формирование субъективного представления о конкретных событиях и на переживание этих событий. Следовательно, педагогически осмысленные и адекватно реализованные динамичные компьютерные визуализации содействуют формированию, развитию или восстановлению когнитивных структур личности в ходе образовательной активности [3]. Это означает, что зрительные образы способны играть роль не только подручного стимульного материала, инициирующего активность учащихся. Они являются наглядно представляемыми объектами, исследуя которые сами учащиеся могут вводить соответствующие математические понятия, характеризовать их и интерпретировать. В ходе такой деятельности учитель не обучает, он организует и педагогически сопровождает.
Проиллюстрируем сказанное на примере освоения понятий «линейная функция» и «угловой коэффициент уравнения линейной функции» в 7 классе. Ниже описана методика, пригодная для работы с различными классами (по составу учащихся и по уровню их знаний).
Возможны различные варианты организации работы учащихся. По нашему мнению, высокую производительность описанной ниже деятельности обеспечивает групповой метод.
Учащиеся в классе разбиваются на малые группы по 4–6 человек.
На первом шаге всем группам предъявляется следующая анимация. В одной и той же системе координат, периодически сменяя друг друга, возникают графики трех линейных функций. При этом аналитические выражения этих функций (y = 0,5x, y = 2x, y = –x) не предъявляются учащимся.
Учитель просит участников групп, чтобы они в группах посовещались и решили, какие это объекты – одинаковые или разные. Тем группам, которые выбрали ответ «разные», учитель предлагает указать, в чем состоят различия. Учащиеся сами определяют, что объекты не совпадают, что они по-разному расположены. А тем группам, которые выбрали ответ «одинаковые», учитель предлагает определить, что объединяет показываемые объекты. Учащиеся сами отмечают, что все объекты – это прямые линии.
Если же все группы выбрали один и тот же вариант ответа, то учитель для всех групп ставит вопрос, альтернативный сделанному выбору. Например, при выбранном ответе «одинаковые» учитель задает вопрос: «Есть ли какие-либо различия между этими объектами?».
Заметим, что уже на первом шаге учитель, не акцентируя внимание учащихся, готовит материал для содержательной рефлексии на тему: «На все ли вопросы о реальных объектах существует один-единственный верный ответ?»
На втором шаге одной трети групп предъявляется анимация функции y = 0,5x, еще одной трети групп – анимация функции y = 2x, оставшейся одной трети групп – анимация функции y = –x. На анимации точка движется по линии, фиксируясь в положениях x = –4; –3; –2; –1; 0; 1; 2; 3; 4. Появляются пунктирные линии, обеспечивающие соответствующие проекции текущего положения точки на координатные оси.
После первого демонстрационного просмотра учитель просит каждую группу составить таблицу пар значений y и x. После того, как такая таблица составлена, учитель предлагает проанализировать ее и определить, что общее у всех пар значений. Ведь эти пары получены для одной и той же линии.
Возможно, в одной группе или в нескольких в ходе обсуждения учащиеся обнаружат, что отношение 
для всех точек одинаковое. Тогда остается записать это в виде, например,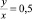 
или y = 0,5x.
Если же ни одна из групп не выявит общего свойства, то учитель предлагает исследовать, можно ли с помощью какого-либо из четырех действий арифметики так связать значения y и x, чтобы получилось общее свойство.
Теперь на третьем шаге учитель говорит учащимся о том, что выражение y = 0,5x (или другое конкретное выражение) получено на основании анализа координат нескольких точек, принадлежащих рассматриваемой прямой. По сути, оно является предположением (гипотезой) о том, что такая запись справедлива для всех точек этой прямой. Учитель просит учащихся дома подумать о том, как доказать справедливость такой гипотезы (первая часть домашнего задания).
На четвертом шаге в демонстрационной анимации последовательно появляются и остаются на экране изображения трех рассматриваемых прямых. Одновременно с появлением каждой прямой появляется ее уравнение, найденное учащимися. Учитель предлагает по группам определить, что общее в этих уравнениях и чем они отличаются.
Учащиеся формулируют, что y и x во всех уравнениях входят одинаково (это общее) и что числовые коэффициенты в уравнениях разные. Учитель просит подумать, можно ли ввести единое название для этих уравнений.
Опираясь на вид графика, учащиеся предлагают название «прямолинейная функция». Учитель принимает ответ как верный и уточняет, что в науке закрепилась укороченная версия названия «линейная функция».
Если же учащиеся сами не формируют название, то учитель задает уточняющий вопрос: «Нельзя ли придумать название, исходя из вида графика этих функций?»
На пятом шаге учитель снова обращает внимание учащихся на то, что, хотя все графики описывают функцию одного и того же вида (линейную), но они имеют разную аналитическую форму. «Подумайте, как обобщить эти формы и одним выражением описать эти функции» – говорит учитель. Одна или несколько групп предлагают запись: y = k•x.
Если ученики не догадываются ввести буквенное обозначение для коэффициента, то учитель предлагает на любом графике описать конкретную точку (например, для x = 1). «А что мы делаем, чтобы описать произвольную точку на том же графике?» – «Используем буквенное обозначение x, которое может принимать любое нужное значение». – «Нельзя ли сделать что-то подобное и с уравнениями?»
На шестом шаге учитель предъявляет анимацию, в которой две точки скользят по двум прямым слева направо: одна точка движется по прямой (а), а вторая точка – по прямой (b). Учитель спрашивает, что общего у функций (a) и (b). После обсуждения в группах ученики сообщают, что обе функции возрастающие.
Если обсуждение не приводит к результату, учитель просит определить, как меняются при движении значения x. Затем он предлагает определить, как меняются при движении значения y. «Какой вывод можно сделать из того, что при движении значения x растут, и значения y растут?» – спрашивает учитель.
На седьмом шаге учитель предъявляет анимацию, на которой точка движется слева направо по прямой (c). Учитель спрашивает, как ведут себя значения x и y в этом случае. Какой вывод можно сделать из того, что при движении значения x растут, а значения y уменьшаются? – спрашивает учитель. После обсуждения ученики сообщают, что функция (c) убывающая.
На восьмом шаге учитель предлагает учащимся поэкспериментировать с другими возрастающими (а затем и убывающими) линейными функциями (по их выбору). Учащиеся выбирают 2–3 целочисленные точки в первом квадранте координатной плоскости (для возрастающих функций) и 2–3 целочисленные точки во втором квадранте (для убывающих функций). Через каждую выбранную точку и начало координат проводят соответствующую прямую линию и определяют ее уравнение.
Результатом экспериментов становятся 4–5 уравнений для возрастающих линейных функций и столько же уравнений для убывающих линейных функций. Учитель просит сравнить первую группу уравнений со второй группой уравнений и определить, что общего у уравнений для возрастающих функций и чем они отличаются от уравнений для убывающих функций. Учащиеся высказывают догадку о том, что, возможно, дело в том, положителен или отрицателен коэффициент k.
Если такая догадка учащимися не высказывается, учитель предлагает определить тот признак, который объединяет все возрастающие функции в одну группу, а все убывающие функции – в другую группу.
Учитель просит учащихся дома подумать о том, как доказать справедливость догадки о том, что при k > 0 уравнение y = k•x описывает возрастающую линейную функцию, а при k < 0 – убывающую линейную функцию (вторая часть домашнего задания).
На заключительном девятом шаге учитель обращает внимание учащихся на все рассмотренные графики. Он просит определить, что изменяется при переходе от одной прямой к любой другой. В ходе обсуждения учащиеся приходят к выводу, что изменяется угол между прямой и осью x. Теперь учитель предлагает обратить внимание на уравнения этих прямых и задает вопрос о том, что изменяется в уравнениях при переходе от одного из них к любому другому. В ходе обсуждения учащиеся приходят к выводу, что изменяется численное значение коэффициента k.
Учитель просит подумать, как можно назвать коэффициент k. Учащиеся предлагают название «коэффициент угла графика». Учитель принимает ответ как верный и уточняет, что в науке закрепилось название «угловой коэффициент».
Общая рефлексия класса позволяет учащимся осмыслить процедуры своей работы. Учащиеся легко осознают, что выполняли сравнение объектов, устанавливали признаки, по которым эти объекты можно объединять, и признаки, по которым они различаются. Учащиеся экспериментировали, создавая новые объекты того же класса. Строили классификацию объектов (возрастающие функции; убывающие функции). Определяли признаки, с помощью которых объекты можно отнести к классу возрастающих функций или к классу убывающих функций.
По сути, в ходе занятия шло активное освоение участниками операций классификации, анализа и синтеза, поиска и выделения необходимой информации. Вырабатывалось умение анализировать ход и способ своих и совместных действий. В то же время работа в малых группах и общие обсуждения создавали реальные условия для формирования умений вступать в диалог, договариваться несиловыми методами, создавать устные и письменные высказывания, выражать свои мысли, строить высказывания в соответствии с задачами коммуникации. Развивались умения слушать и слышать.
Таким образом, реализация описанного подхода органично и естественно обеспечивает ориентацию и на достижение предметных (математических) образовательных результатов, и на овладение универсальными способами деятельности, обеспечивающими успешность в различных видах целенаправленной человеческой активности. А достаточно продолжительная практика такого рода способна существенно изменить и отношение учащихся к математике.