Сложные производственные процессы характеризуются многостадийностью обработки, при которой на каждом агрегате или стадии обработки существует свой набор технологических параметров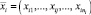 
, где i = 1, 2, ..., N – индекс агрегата или стадии обработки; N – количество стадий; j = 1, 2, ..., ni – индекс технологического параметра для i-го агрегата или стадии обработки; ni – количество технологических факторов на данном переделе. Набор выходных свойств продукции (показателей качества) можно описать как y = (y1, ..., ym). Тогда производственные процессы можно представить (рис. 1) в виде цепочки стадий обработки или агрегатов [1–10].
Каждая случайная технологическая величина изменяется в определенных границах: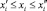 
. Для идентификации технологии осуществляется выбор исходных границ, образующих подпространство 
:
,
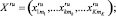
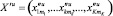где k – номер стадии обработки; jk – j-я случайная технологическая величина k-й стадии обработки.
На первом этапе для каждой случайной технологической величины определяются минимальные и максимальные значения по исследуемой выборке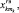 
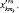Затем этот диапазон изменения входной величины разбивается на ряд составляющих алфавитов:
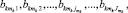
где k – номер стадии обработки; mk – случайная величина k-й стадии обработки;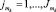 
– номера составляющих алфавита данной величины.
Рис. 1. Схема многостадийной обработки
Каждая выделенная составляющая алфавита
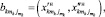
где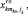 
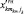– границы выделенной 
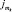-й составляющей алфавита; н – начальная установка:
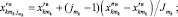
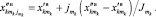
Для каждой составляющей алфавита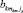 
определяется свое 
.
Задача дискретной оптимизации сводится к определению такого технологического подпространства Ξ* (таких границ случайных величин
(
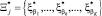
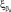– вариант сочетания алфавитов на k-м агрегате), для которого целевая функция (критерий оценки эффективности режимов функционирования сложных систем) принимает максимальное значение:
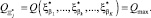
Критерий оценки эффективности режимов функционирования сложных систем представляется в виде
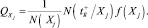
Определяется количество, попавших в оптимальное подпространство свойств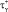 
, т.е. 
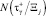, из общего количества точек в исследуемом подпространстве N(Ξj).
Для того чтобы суммарный критерий учитывал число точек, удовлетворяющих технологии (Ξ*), его необходимо также помножить на штрафной коэффициент, который понижает критерий при малом числе попавших точек и повышает – при большом. В качестве такого «штрафа» использована функция
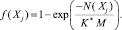
Насыщение (значение стремится к 1,0) данной функции происходит примерно в точке –K*M, где M – количество экспериментальных значений (объем выборки); K – доля объема выборки (например, K = 0,1).
Данное соотношение можно продемонстрировать на графике.
Таким образом, можно выделить сочетания алфавитов технологических параметров ξβ, которые позволяют получать оптимальное сочетание выходных алфавитов
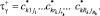
Необходимо подобрать технологическую цепочку Ξ* из набора сочетаний алфавитов технологических величин, обеспечивающую максимальную вероятность попадания в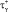 
. Используется метод сеток, состоящий в построении сетки подмножеств, вычислении значений целевой функции в каждом из них и выборе лучшего.
Пример формирования сетки подмножеств приведен в табл. 1. Рассматриваются четыре случайных величины, алфавит каждой из которых равен двум или трем.
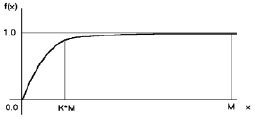
Рис. 2. График распределения штрафной функции
Таблица 1
Пример формирования сетки подмножеств для первых четырех технологических факторов
|
X1X2X3X4 |
N(Xj) |
|
|
QXj |
X1X2X3X4 |
N(Xj) |
|
|
QXj |
|
K = 2 |
K = 3 |
||||||||
|
0000 |
36 |
13 |
36,111 |
0,184 |
0000 |
0100 |
44 |
36,364 |
0,211 |
|
0001 |
2 |
0 |
0,00 |
0 |
0001 |
0110 |
6 |
33,333 |
0,037 |
|
0100 |
110 |
61 |
55,455 |
0,492 |
0100 |
0122 |
1 |
100 |
0,019 |
|
0101 |
42 |
22 |
52,381 |
0,296 |
… |
… |
… |
… |
… |
|
0111 |
1 |
1 |
100 |
0,019 |
0111 |
1100 |
176 |
52,273 |
0,506 |
|
1000 |
59 |
22 |
37,288 |
0,257 |
… |
… |
… |
… |
… |
|
1001 |
8 |
2 |
25,000 |
0,036 |
2200 |
39 |
18 |
46,154 |
0,248 |
|
1100 |
221 |
101 |
45,701 |
0,451 |
2201 |
7 |
7 |
100,000 |
0,129 |
|
1101 |
25 |
20 |
80,000 |
0,312 |
2202 |
2 |
1 |
50,000 |
0,019 |
, %
, %Процедуры поиска границ очень сложно реализовать для всех факторов многостадийной технологии. Если стадий обработки много, то необходимо процедуры выбора оптимальных границ проводить по отдельным агрегатам. Если начать процедуру поиска с первого агрегата, то полученные оптимальные диапазоны изменения его факторов, как правило, оказываются уже диапазонами изменения по выборке.
В рассмотренном примере для технологических факторов X1X2X3X4 лучшим является сочетание (0111) для K = 3 при значении критерия оценки эффективности режимов функционирования сложных систем, равном 0,506. В данное подмножество попало 176 опытов. Как видно, при K = 2 максимальное значение критерия наблюдается для 0,492 и сочетания факторов (0100), что меньше, чем при K = 2, что говорит о том, что для факторов X1X2X3X4 увеличение размерности алфавита приводит к увеличению значения критерия и оптимизации технологии. В общем случае увеличение размерности алфавита не может гарантировать увеличение значения критерия, как будет видно из следующего примера, однако есть возможности выбора иных алгоритмов построения сетки (например, с использованием достаточно сложной формы подпространств сетки разбиения), которые могут позволить получить более точное решение рассматриваемой задачи оптимизации сложной многостадийной технологии.
Далее выполняется поиск оптимальных границ на следующем этапе со «сжатием» диапазонов факторов из-за уменьшения исследуемого объема выборки.
Пример формирования сетки для следующих четырех переменных приведен в табл. 2.
Таблица 2
Пример формирования сетки подмножеств для следующих четырех технологических факторов
|
X5X6X7X8 |
N(Xj) |
|
|
QXj |
X5X6X7X8 |
N(Xj) |
|
|
QXj |
|
K = 2 |
K = 3 |
||||||||
|
0000 |
9 |
8 |
88,889 |
0,355 |
0010 |
5 |
5 |
100,000 |
0,247 |
|
0010 |
2 |
2 |
100,000 |
0,107 |
0100 |
4 |
4 |
100,000 |
0,203 |
|
0100 |
30 |
20 |
66,667 |
0,545 |
0110 |
4 |
3 |
75,000 |
0,152 |
|
0101 |
2 |
1 |
50,000 |
0,053 |
… |
… |
… |
… |
… |
|
0111 |
36 |
5 |
13,889 |
0,120 |
1110 |
20 |
14 |
70,000 |
0,475 |
|
1000 |
27 |
14 |
51,852 |
0,406 |
… |
… |
… |
… |
… |
|
1011 |
1 |
1 |
99,999 |
0,055 |
2212 |
1 |
0 |
0 |
0 |
|
1100 |
36 |
23 |
63,889 |
0,556 |
2221 |
5 |
3 |
60,000 |
0,148 |
|
1101 |
1 |
1 |
100 |
0,055 |
2222 |
10 |
6 |
60,000 |
0,260 |
, %
, %В результате проведения всех расчетов и сравнения между собой критериев оценки эффективности режимов функционирования сложных систем, рассчитанных для подпространств, полученных в результате разбиения пространства качества с различными алфавитами K, определяется оптимальное сочетание факторов, представляющее из себя оптимальную технологию производства продукции заданного качества.
Для технологических факторов X5X6X7X8 при алфавите для каждого фактора, равном двум (K = 2), максимальное значение критерия 0,556 достигается для сочетания (1100), при K = 3 значение критерия максимально (0,475) для (1110). Как видно, в данном случае применение алфавита, равного двум, дало лучшие результаты оптимизации технологии для факторов X5X6X7X8, и увеличение размерности алфавита не привело к увеличению значения критерия, т.е. оптимальная технология определяется сочетанием (1100) для K = 2.
Итоговая оптимальная технология для двух переделов определяется сочетанием (01111100), где сочетание (0111) – оптимальная технология на первом переделе для факторов X1X2X3X4, достигаемое при алфавите K = 3, и сочетание (1100) – оптимальная технология для факторов X5X6X7X8 на втором переделе, достигаемое при K = 2.
Поскольку оптимизация на втором этапе производилась со «сжатием» диапазонов факторов из-за уменьшения исследуемого объема выборки, можно сказать, что на втором этапе производилась условная оптимизация, в качестве дополнительного условия выступало условие реализации на первом переделе оптимальной технологии, т.е. сочетания (0111) технологических факторов X1X2X3X4. Это условие иллюстрирует статистическую связь переделов в методах оптимизации многоступенчатой технологии.
Таким образом, в настоящей работе:
1) разработаны алгоритмы поиска оптимальных режимов сложных промышленных систем с использованием в качестве параметров оптимизации подпространств, образованных случайными величинами;
2) предложен метод выбора оптимальных подпространств на отдельных этапах обработки с учетом поиска оптимальных режимов на предыдущих этапах.
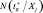
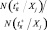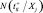
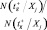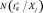
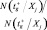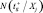
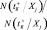