Методы идентификации наночастиц серебра, рассмотренные в работах [3–7], не дают достаточной чувствительности при определении режимов нанесения наночастиц на поверхность полиэфирных волокон. Поэтому в работе предлагается способ повышения чувствительности идентификации наночастиц с использованием метода составления системы уравнений в векторно-матричной форме записи системы нелинейных квадратических выражений с оценкой плотности вероятности пересечения эллипсов распределения пиков рамановского поляризационного спектра на основе корреляционных данных об обьекте системы наночастицы – полиэфирное волокно.
Цель работы – повышение достоверности распознавания наночастиц серебра на поверхности текстильных материалов на основе проведения статистического моделирования корреляционных параметров интенсивности спектров полиэфирного волокна.
Материалы и методы исследования
Для проведения эксперимента были выбраны полиэфирные волокна (ПЭ), на которые нанесли коллоидный раствор, содержащий наночастицы серебра. В региональном центре нанотехнологий при ЮЗГУ с использованием сканирующего зондового микроскопа (СЗМ) с конфокальным рамановским и флуоресцентным спектрометром OmegaScope™ – были получены рамановские спектры полиэфирных волокон, покрытых и не покрытых наночастицами серебра. Всего для исследования было выделено девять информативных пиков.
В ходе предварительного исследования были определены корреляционные матрицы и параметры распределений (математические ожидания и средние квадратические отклонения) рамановских спектрограмм с учетом поляризации излучения поперек и вдоль волокон одновременно за одно измерение [9, 10].
На следующем этапе осуществлено моделирование статистических данных для выявления пересечений эллипсов распределений значений интенсивностей пиков спектрограмм [1–2]. Генерация заданного количества случайных значений проводилась по нормальному закону с использованием встроенных функций математического редактора MathCad Edition 14, а также методике, предложенной авторами статьи и изложенной в работе [8].
Для выявления R – радиуса кривизны пересечения эллипсов распределения необходимо записать его в векторно-матричных аналитических выражениях по координатам точек пересечения. В данной работе рассматривается система только двух векторно-матричных аналитических выражений R2 = XT·Σ–1·X для p0 и p1.
Реализованное решение в общем виде с использованием встроенных функций программного продукта MathCad Edition 14 представлено выражениями (1)–(3). При этом использованы следующие обозначения: rXY, rXYAg – корреляционные матрицы рамановских поляризационных спектров полиэфирных волокон без наночастиц серебра и с наночастицами серебра соответственно; MENX, MENXAg – математические ожидания интенсивности пиков спектров с поляризацией поперек волокон Х без наночастиц серебра и с наночастицами серебра соответственно; MENY, MENYAg математические ожидания интенсивности пиков спектров с поляризацией вдоль волокон Y без наночастиц серебра и с наночастицами серебра соответственно; σΔX, σΔXAg – средние квадратические отклонения интенсивности пиков спектров с поляризацией поперек волокон Х без наночастиц серебра и с наночастицами серебра соответственно; σΔY σΔYAg – средние квадратические отклонения интенсивности пиков спектров с поляризацией вдоль волокон Y без наночастиц серебра и с наночастицами серебра соответственно; i – номер пика спектрограммы.
Аналитическая оценка p0 и p1 – плотностей вероятностей по точкам пересечения эллипсов распределений производится по векторно-матричным аналитическим выражениям:
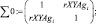
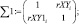 (1)
(1)
р: = –4.6366281 i: = 0;
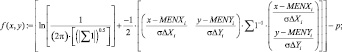 (2)
(2)
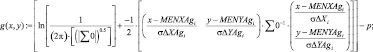 (3)
(3)
x: = 470.0 y: = 470.0
Given
f(x, y) = 0 g(x, y) = 0
v2: = Find(x, y)

f(v20, v21) = –4.532×10–4
g(v20, v21) = –9.999×10–4 (4)
Радиус кривизны для точки пересечения эллипсов распределения интенсивностей переизлучения рамановских спектров приведен в выражениях
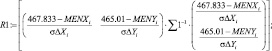 (5)
(5)
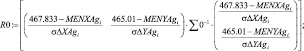 (6)
(6)
R1 = 2.953136 R2 = 2.442229
Плотность вероятности для точки пересечения эллипсов распределения интенсивностей переизлучения рамановских спектров приведена в выражениях
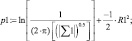 (7)
(7)
p1 = –4.637101 ep1 = 9.6857363×10–3 1 – 9.6857363×10–3 = 0.990314;
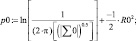 (8)
(8)
p0 : = –4.637619 ep0 = 9.68071879×10–3 1 – 9.68071879×10–3 = 0.990319.
Результаты исследования и их обсуждение
При векторно-матричном моделировании аналитического пересечения эллипсов распределения с решением системы уравнений при равенстве плотностей вероятностей эллипсов распределения p1 = p0 получены координаты по девяти пикам:
для поперечной поляризации Х
XLnT = (467.833 185.989 258.451 394.003 448.954 557.808 614.384 346.974 692.274); (9)
для продольной поляризации Y
YLnT = (465.010 367.542 748.514 1975.35 2554.92 1047.91 1102.10 103.662 152.334). (10)
Критериями пересечения эллипсов распределения при решении уравнений являются плотности вероятности p1 = p0 = р.
pT = (9.69•10–3 0.0699 0.0113 5.289•10–4 0.0207 1.139•10–3 0.0331 1.057•10–3 1.625•10–3), (11)
а вероятности пересечения эллипсов будут
QT = (0.99031 0.93011 0.98866 0.99947 0.97927 0.99886 0.96689 0.99894 0.99837). (12)
Эквивалентный радиус эллипсов (6) при пересечении для волокна без наночастиц
R0LnT = (2.442 1.285 2.317 3.413 2.023 3.196 1.773 3.168 3.029) (13)
и эквивалентный радиус эллипсов (5) при пересечении для волокна с наночастицами
R1LnT = (2.953 1.588 2.767 3.815 2.733 3.455 2.700 3.399 3.274). (14)
Средний эквивалентный радиус эллипсов (2) при пересечении для волокна без наночастиц и с наночастицами
RсрLnT = (2.697 1.437 2.542 3.614 2.378 3.325 2.236 3.284 3.151). (15)
Для точки пересечения эллипсов распределения оценены по плотности вероятностей (7) и (8)
p1T = (9.6857•10–3 0.069816 0.0113263 5.2857•10–4 0.020717 1.1375•10–3 0.033087 1.056346•10–3 1.62383•10–3), (16)
p0T = (9.6807•10–3 0.069826 0.0113234 5.2835•10–4 0.020713 1.1376•10–3 0.033073 1.055722•10–3 1.62317•10–3). (17)
Выводы
В работе предложен векторно-матричный метод повышения достоверности распознавания наночастиц серебра на поверхности полиэфирных волокон при приведении моделирования по многомерным корреляционным составляющим рамановских спектров. Проведена оценка достоверности идентификации наносеребра на волокнах полиэфира с учетом поляризации луча. На рисунке представлены графические результаты повышения информативности оценки определения достоверности.
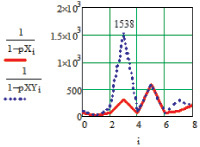 а
а 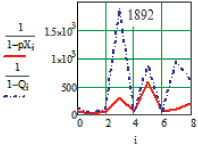 б
б
Повышение информативности оценки достоверности при применении двухмерного измерения
При этом на данных графиках используются следующие обозначения: на рисунке а, б сплошной линией ---- представлены измерения при поперечной поляризации Х с генерацией многомерных корреляционных данных; на рисунке а, б линиями …. и -.-.- соответственно показаны измерения в поперечном Х и продольном Y направлениях с учетом коэффициентов корреляции и эквивалентного радиуса эллипса в точке пересечения эллипсов распределения.
Таким образом, можно сделать вывод, что предложенный метод дает существенный выигрыш в оценке достоверности определения режимов нанесения наночастиц серебра на волокна. Например, для 4 пика увеличение произошло в 1892 раза.



