Для выбора рациональных алгоритмов управления системами отопления зданий и сооружений необходимы математические модели нестационарных тепловых процессов в ограждающих конструкциях. Использование математических моделей ограждающих конструкций как объектов с сосредоточенными параметрами, когда решаются обычные дифференциальные уравнения, позволяет разрабатывать только упрощенные алгоритмы управления системами теплоснабжения зданий и сооружений [4]. Для оптимального управления температурным режимом каждого объекта требуется знать характеристики, получить которые можно математическим моделированием процессов переноса тепла через ограждения здания решением дифференциальных уравнения в частных производных.
Для исследования процессов теплопередачи через ограждение решается уравнение теплопроводности при граничных условиях 3-го рода, когда задаются температуры среды и коэффициенты теплоотдачи [2, 5]. В условиях несимметричного теплообмена плоская стенка здания толщиной d (рис. 1) с коэффициентом теплопроводности l, удельной теплоемкостью с и плотностью r омывается с внутренней поверхности средой с температурой Т1, с внешней поверхности - средой с температурой Т2. При этом Т2 ≠ Т1.
Передача тепла от воздуха в помещении к внутренней поверхности стенки характеризуется коэффициентом теплоотдачи a1. Передача тепла от внешней поверхности стенки к наружному воздуху характеризуется коэффициентом теплоотдачи a2. В общем случае несимметричного теплообмена α1 ≠ α2 [2, 5].
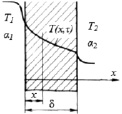
Рис. 1. Теплопередача через плоскую стенку
Для одномерного нестационарного температурного поля в области 0 < х < δ при τ > 0 температурное поле описывается уравнением
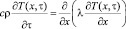. (1)
Начальное условие 0 ≤ х ≤ δ и τ = 0
Т(х,0) = f(x). (2)
Граничные условия:
при х = 0
;
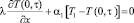при х = δ
.
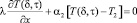Для решения дифференциального уравнения с несимметричными граничными условиями используется принцип суперпозиции, согласно которому решение представляется в виде суммы решения стационарной задачи для функции V(х) с заданными граничными условиями и нестационарной задачи для функции W(х, t) с нулевыми граничными условиями [2, 5, 6]:
Т(х, t) = V(х) + W(х, t). (3)
Функция V(х) описывает установившийся стационарный режим, а функция W(х, t) – переходный тепловой процесс, по окончании которого функция W(х, τ) стремится к нулю.
При допущении однородности среды нестационарное температурное поле в области 0 < х < δ при τ > 0 описывается уравнением
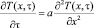, (4)
где a – коэффициент температуропроводности.
Функция V(x) является решением уравнения
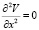. (5)
При граничных условиях
при х = 0
,
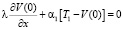при х = δ
.
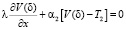Функция V(x) имеет вид
. (6)
Решение стационарной задачи позволяет рассчитывать тепловое поле в стенке в установившемся режиме. Коэффициент A в формуле (6) численно равен температуре на наружной поверхности стенки, коэффициент B – градиенту температуры в объеме стенки.
Коэффициенты А и В в формуле (6) определяются по выражениям
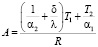(7)
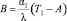, (8)
где R – тепловое сопротивление теплопередачи в стационарном режиме,
.
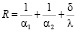Если тепловой переходный процесс начинается с установившегося режима при температурах внутреннего и наружного воздуха соответственно T1нач и T2нач, то коэффициенты Aнач и Bнач определяются по формулам
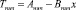, (9)
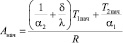, (10)
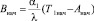. (11)
При изменении температуры наружного воздуха в стенке наступает переходный тепловой процесс, по окончании которого температура по сечению распределяется по линейному закону.
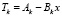, (12)
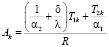, (13)
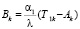. (14)
При изменении условий теплообмена, когда меняются температуры наружного воздуха или (и) температуры воздуха внутри помещения, происходит переход от одного установившегося состояния к другому. Тепловой переходный процесс описывается функцией W(х, τ), которая находится решением уравнения
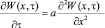. (15)
Начальное условие 0 ≤ х ≤ δ и τ = 0
W(х,0) = f(x) – V(x). (16)
Граничные условия:
при х = 0
,
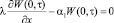при х = δ
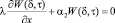. (17)
Граничные условия (17) выполняются, если функция W(x, τ) имеет вид
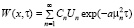, (18)
где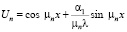 
,
μn – корни характеристического уравнения [2]
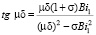, (19)
где s = a2/a1 – критерий несимметричности теплообмена;
Вi1 = a1d/l – критерий Био для внутренней поверхности стенки.
Коэффициенты Cn определяются из начальных условий. Теоретическое решение имеет вид бесконечного ряда [2, 5, 6]:
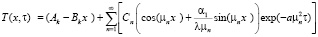. (20)
Для реализации начальных условий функция W(х, 0) = f(x) – V(x) теоретически может быть представлена в виде ряда (20), однако для несимметричных граничных условий третьего рода применение метода разделения переменных Фурье и других аналитических методов наталкивается на серьезные трудности [1]. Решения получаются в виде бесконечных рядов, которые плохо сходятся в начальный период времени, поскольку для реализации начальных условий применяется разложение в ряд Фурье разрывных функций. При этом наблюдается явление Гиббса, когда представленная тригонометрическим рядом функция, проходя через точку разрыва, делает скачок [1]. Теоретически точное решение на практике оказывается приближенным. Поэтому вместо нахождения точных аналитических решений применяются приближенные аналитические решения краевых задач, которые отличаются от точных решений на некоторую малую величину Р(х) погрешности [3].
Для расчета нестационарного температурного поля в стенке при несимметричных граничных условиях третьего рода и любых начальных условиях наиболее целесообразно искать решение уравнения (1) по методу Треффтца [3] в виде конечной суммы, каждое слагаемое которой удовлетворяет уравнению (1) и граничным условиям третьего рода.
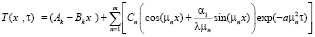. (21)
При этом функция W(x,τ) имеет вид
.
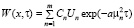Для реализации начального условия коэффициенты Cn определяются решением системы линейных уравнений, полученной приравниванием значений функции Т(хm, 0) и значений заданных начальных условий f(xm) в определенных точках xm.
Для реализации начального условия (16) в общем случае должно выполняться равенство:
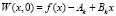. (22)
Если начальным условием является линейное распределение температуры по толщине стенки
,
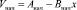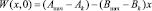. (23)
Для нахождения коэффициентов Сn решается система линейных уравнений
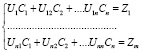, (24)
где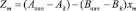 
.
Система (35) представляется в матричном виде:
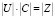. (25)
Эта система легко решается через обратную матрицу [1]
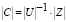. (26)
Для расчета изменения во времени теплосодержания стенки в течение переходного процесса необходима среднеинтегральная температура стенки [2]:
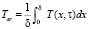, (27)
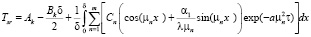. (28)
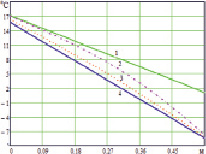
Рис. 2. Распределение температуры по толщине стенки для различных моментов времени при похолодании: 1 – начальное стационарное распределение температуры перед началом теплового переходного процесса, 2 – распределение температуры через 4 часа после начала теплового переходного процесса, 3 – распределение температуры через 12 часов после начала теплового переходного процесса, 4 – конечное стационарное распределение температуры после окончания теплового переходного процесса
По формулам (21) и (28) рассчитаны распределения по температуры по толщине стены здания (рис. 2) и зависимости от времени температуры на внутренней поверхности стены, среднеинтегральной температуры, средней температуры стены и температуры на наружной поверхности стены (рис. 3).
При похолодании, когда температура наружного воздуха изменяется от 0 °С до – 10 °С, температура на внутренней поверхности выходит на установившееся значение более двух суток (рис. 3), температура на внешней поверхности за 12 часов уже практически достигает установившегося значения. Из приведенных на рис. 3 зависимостей от времени среднеинтегральной температуры Tsr при протекании теплового переходного процесса видно, что в процессе перехода от одного установившегося режима к другому среднеинтегральная температура и соответственно теплосодержание стенки меняются в течение более двух суток. Постоянная времени для среднеинтегральной температуры – 27 часов. Вследствие нелинейного закона распределения температуры по сечению в начале переходного процесса средняя и среднеинтегральная температура стены различаются и становятся одинаковыми по окончании переходного процесса. В течение теплового переходного процесса меняются температуры внутренней и наружной поверхностей стены, вследствие этого удельные тепловые потоки от воздуха в помещении к внутренней поверхности стенки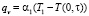 
и от наружной поверхности стены к наружному воздуху 
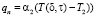также меняются во времени (рис. 4), причем до окончания переходного процесса эти потоки резко различаются и становятся одинаковыми только по окончании переходного процесса. Поэтому понятия тепловое сопротивление стены и коэффициент теплопередачи могут применяться только в установившемся режиме, который наступает через десятки часов после изменения теплового режима.
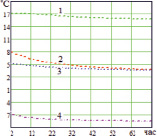
Рис. 3. Зависимости от времени температуры на внутренней поверхности стенки (1), среднеинтегральной температуры (2), средней температуры стенки (3) и температуры на наружной поверхности стенки (4)
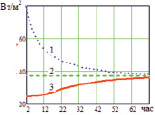
Рис. 4. Зависимость от времени удельных тепловых потоков через наружную поверхность стены (1), внутреннюю поверхность (3) и при установившемся режиме (2)
Выводы
Разработана математическая модель нестационарных тепловых процессов в ограждающих конструкциях при несимметричных граничных условиях третьего рода и различных начальных условиях. Решением дифференциального уравнения в частных производных получены зависимости от времени распределения температуры по объему наружной стены здания при изменении температуры наружного воздуха. Показано, что стена является объектом с распределенными параметрами, температура на внешней поверхности стены достигает установившегося значения через несколько часов, на внутренней поверхности через десятки часов после начала теплового переходного процесса. Коэффициент теплопередачи ограждения может быть определен только для установившегося теплового режима.
Работа выполнена при поддержке Фонда содействия развитию малых форм предприятий в научно-технической сфере, грант УМНИК 2015.