Для современных направлений производства, например, промышленной робототехники, актуальным является использование новых типов мультикоординатных электродвигателей, позволяющих преодолеть ограничения подвижности конструкции, вызванные наличием только одной степени свободы у традиционных источников движения [2]. Идея использования мультикоординатного электродвигателя (МКД) заключается в управлении положением ротора посредством изменения конфигурации магнитного поля статора [8, 9].
К конструкции МКД (рис. 1, а) предъявляются следующие требования. Во-первых, это обеспечение управляемого углового перемещения ротора с тремя степенями свободы (рис. 1, б) с высокой точностью позиционирования [1]. Во-вторых, ротор должен обладать полной управляемостью и плавностью хода, а также развивать требуемый момент на валу [7]. Этим требованиям отвечает конструкция, предложенная в статье [4] и являющаяся развитием идеи, изложенной в работе [10]. В рассматриваемом МКД число полюсов ротора и их расположение определяется вписанным правильным многогранником, а для распределения электромагнитов по поверхности статора предполагается использовать либо тот же принцип, либо условно-равномерное распределение [3, 5].
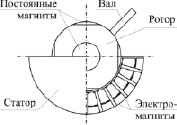
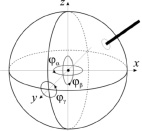
а) б)
Рис. 1. Мультикоординатный электродвигатель: а) конструкция; б) координаты
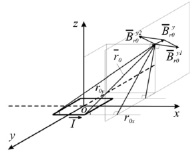
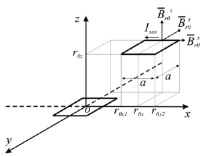
а) б)
Рис. 2. Векторные диаграммы
Математическое описание такой системы является необходимым условием для построения систем управления МКД [6], а также их внедрения в автоматизированные производства. Построение требуемого математического описания состоит из составления трех математических моделей. Первая модель описывает взаимодействия электромагнита и постоянного магнита для определения оптимальной конфигурации полюсов ротора и статора, а также определения сил взаимодействия между ними. Вторая модель описывает процессы, протекающие в отдельной катушке статора для формирования требуемых сил взаимодействия между статором и ротором. Третья модель описывает динамику изменения угловых координат ротора при заданных силовых воздействиях и требуется для управления движением МКД.
Математическая модель взаимодействия постоянного магнита и электромагнита
Магнитное поле, создаваемое электромагнитом, неоднородно, поэтому для создания необходимой модели была выведена формула расчета магнитной индукции, создаваемой прямоугольным витком в произвольной точке пространства на основе закона Био-Саварра-Лапласа. В ходе преобразований получены две составляющие результирующего вектора магнитной индукции, на основе которых получены проекции составляющих вектора магнитной индукции по трем осям (рис. 2, а):
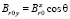 ;
; 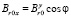 ;
;
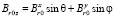 , (1)
, (1)
где 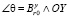 ,
, 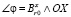 .
.
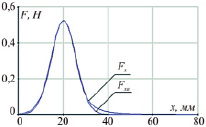
Рис. 3. Зависимость силы взаимодействия от расстояния смещения
Адекватность (1) была подтверждена экспериментально. Индукция магнитного поля была измерена при помощи цифрового датчика Холла марки 435G TO92. При его прямолинейном перемещении над поверхностью электромагнита, с датчика снимались данные о модуле магнитной индукции. Электромагнит был изготовлен специально для эксперимента число витков и номинальный ток соответствуют расчетным. Отклонение между расчетными и экспериментальными данными не превысило 8 %.
Описание взаимодействия электромагнита и постоянного магнита с использованием (1) требует замены постоянного магнита одновитковым контуром с эквивалентным током Iэкв согласно методу эквивалентного соленоида (рис. 2, б). Применив указанное допущение на основе закона Ампера рассчитаны составляющие силы взаимодействия Fx и Fy по соответствующим осям. Следует отметить, что пока центр эквивалентного контура находится непосредственно над центром контура электромагнита, силы в плоскости XOY скомпенсированы, суммарная сила взаимодействия направлена вдоль оси Z. Но при смещении возникает сдвигающий момент, формирующий полезное усилие, обеспечивающее угловое перемещение ротора. Для составляющей силы, действующей на круглый магнит вдоль прямой, соединяющей центр электромагнита и проекцию центра постоянного магнита на ось ОХ, была получена зависимость от расстояния смещения Fx = f(x) (рис. 3). Уравнение Fx достаточно громоздко, однако данная зависимость с высокой точностью аппроксимируется функцией Гаусса:
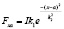 , (2)
, (2)
где k1, k2 – коэффициенты аппроксимации.
Математическая модель электромагнитных процессов в электромагните статора
Описание процессов, протекающих в каждой катушке статора, и сил взаимодействия между статором и ротором опирается на условие, что катушки распределены равномерно и, соответственно, каждая из них окружена шестью соседними, образуя гексогональный базовый сегмент. Влияние на центральную катушку катушек за пределами базового сегмента пренебрежимо мало. Учитывая, что расстояние между центрами катушек одинаково, а следовательно, равна их взаимная индуктивность, составлено уравнение Кирхгоффа:
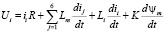 , (3)
, (3)
где Li – индуктивность i-й катушки; ii – ток i-й катушки; Lm – взаимная индуктивность расположенных рядом катушек; K – конструктивный коэффициент, определяемый параметрами сферического двигателя и величиной воздушного зазора; ψm – потокосцепление постоянного магнита.
Для низких скоростей ротора (в работе принято значение 6 рад/с и менее) можно сделать допущение dψm/dt = 0, с учетом которого, а также принимая, что магнитная система не насыщена, а положение постоянных магнитов полюсов ротора не влияет на собственную индуктивность полюсов статора, т.е. Li = const = L, на основе (3) в форме Коши, с помощью метода Гаусса получено выражение
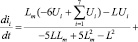
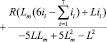 . (4)
. (4)
Так как влияние электромагнитов за пределами базового сегмента на его центральный электромагнит, обозначенный в (3) и (4) номером 1, принято пренебрежимо малым, током статора, формирующим силу F, действующую на полюс ротора, принят ток i1. Именно этот ток подстановкой в (4) используется для расчета F.
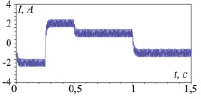
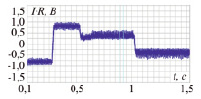
Корректность такого подхода обосновывается адекватностью (4), подтвержденной экспериментально. Моделирование (4) выполнялось в программной среде ScicosLab, где на входы модели в качестве напряжений U1-U7, подводимых к катушкам базового сегмента, были поданы сигналы, соответствующие напряжениям экспериментальной установки, представляющей собой физическую модель базового сегмента. Результаты моделирования и эксперимента приведены на рис. 4, средневзвешенное расхождение между моделью и экспериментальными данными не превышает 10 %.
Математическая модель движения в угловых координатах
Модель перемещения ротора описывает динамику изменения углов φα, φβ и φγ (рис. 1, б) в условиях ограничений, накладываемых поверхностью сферы:
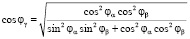 ;
;
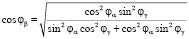 .
.
Учитывая особенности конструкции (рис. 1, а), при составлении модели было сделано допущение, что присоединенный к ротору вал описывается стержнем массой m и длиной l. Ротор массой М и радиусом R образуют с валом систему, для которой можно записать уравнения движения:
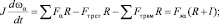
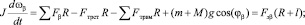
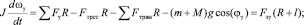 (5)
(5)
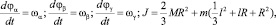
где J – суммарный момент инерции системы; Fα, Fβ, Fγ – суммарная сила, прикладываемая ко всем полюсам ротора по касательной к поверхности ротора в плоскости XOY, ZOY и XOZ соответственно; Fтрст, Fтрвм – составляющая силы трения, определяемая соответственно силой тяжести и взаимодействием постоянных магнитов и железа статора; Fэ – эквивалентная результирующая сила на конце стержня; ωα, ωβ, ωγ – угловые скорости.
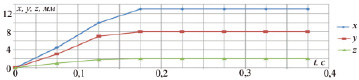
Уравнение (5) совместно с (2) и (4) составляет полное математическое описание электромеханических процессов в мультикоординатном электродвигателе с постоянными магнитами. Адекватность этого описания была подтверждена с использованием опытного образца МКД. В ходе исследований моделировался один шаг ротора, являющийся реакцией на конкретные управляющие воздействия, эквивалентные воздействиям, совершаемым с опытным образцом МКД. Результаты исследования, представленные на рис. 5, демонстрируют, что максимальное расхождение по координатам x, y и z составило 11 %, 10 % и 11 % соответственно.
а) б)
Рис. 4. Переходные процессы: а) ток i1, полученный методом моделирования; б) напряжение i1Rш, снятое с измерительного шунта тока

а)
б)
Рис. 5. Переходные процессы: а) моделирование; б) эксперимент
Таким образом, в работе предложено решение задачи математического описания электромагнитных процессов, протекающих в катушке статора трехкоординатного электродвигателя, получена зависимость полезной составляющей силы взаимодействия полюсов ротора и электромагнитов статора, а также составлено и проверено на адекватность полное математическое описание МКД. Полученные результаты могут использоваться в робототехнике, а также исследованиях, посвященных дальнейшему совершенствованию электромеханических преобразователей, осуществляющих движение одновременно в трех координатах.



