Современная вычислительная математика связана с решением разного рода математических задач с применением ЭВМ. Решаемые математические задачи могут быть классифицированы на следующие основные группы:
- алгебраические (решение уравнений (линейных и нелинейных) и их систем, поиск собственных значений, обращение матриц);
- дифференциальные уравнения (задачи дифференцирования и интегрирования функций одной и нескольких переменных, решение обыкновенных дифференциальных уравнений);
- задачи оптимизации (поиск максимального и минимального значений функции на определенном множестве);
- задачи математического программирования – аппроксимации, интерполяции функций и т.д.
Безусловно, возрастающий объем задач требует автоматизации их решения. В этой связи становится весьма актуальным применение для их решения функциональных программных средств. К их числу относятся математические пакеты Matlab, Mathematica, Scilab и др. Все они содержат необходимый набор методов решения математических задач, а также средства для визуализации и отображения полученных результатов. Наиболее известным среди вышеперечисленных программных средств является математический пакет Matlab. Он позволяет производить различной сложности технические вычисления, содержит одноименный язык программирования, предоставляет большое количество функций анализа данных, связанных практически со всеми областями математики, используется более чем 1 000 000 инженерных работников, поддерживается большинством операционных систем. Однако данный пакет является коммерческим. Разумеется, этот факт затрудняет широкое использование пакета Matlab. Но существуют свободно распространяемые альтернативы данного пакета. В качестве примера можно привести программную систему Scilab.
Scilab – это система компьютерной математики, являющаяся самым полным аналогом пакета Matlab, предназначенная для выполнения научных и инженерных вычислений. В системе Scilab реализованы следующие методы решения вычислительных задач:
- задачи линейной алгебры;
- нелинейные уравнения и системы уравнений;
- обработка экспериментальных данных;
- задачи оптимизации;
- интегрирование и дифференцирование;
- обыкновенные дифференциальные уравнения и их системы.
Scilab позволяет работать с большим числом специальных функций (Бесселя, Неймана и т.д.), имеет средства для построения и работы с графиками. Для выполнения численных расчётов могут использоваться библиотеки Lapack, LINPACK, Atlas и другие. Для решения нестандартных задач имеется встроенный объектно ориентированный язык программирования, sci-язык, с помощью которого пользователь может создавать свое визуальное приложение в виде отдельной программы. Кроме того, в состав Scilab входит утилита, осуществляющая конвертирование документов из Matlab в Scilab, что немаловажно при разработке программ в системе Scilab, использующих готовые модули пакета Matlab.
Рассмотрим более подробно основные возможности программной системы Scilab при решении различных задач вычислительной математики.
1. Решение задач линейной и нелинейной алгебры.
Система Scilab позволяет решать многие задачи линейной алгебры, к которым относятся операции над матрицами (сложение, вычитание, умножение матриц, умножение матрицы на число, возведение в степень, определение определителя, ранга, ядра матрицы, нормы квадратной матрицы, нахождение обратной и псевдообратной матриц, вычисление собственных значений и собственных векторов квадратной матрицы, треугольное разложение матрицы), решение систем линейных уравнений и др. Также Scilab предоставляет возможность решения задач нелинейной алгебры. Это задачи определения корней полинома, решения трансцендентных уравнений, решения систем нелинейных уравнений. Приведем примеры некоторых задач.
Стандартной задачей линейной алгебры является поиск решения системы линейных уравнений.
Допустим, необходимо найти решение системы линейных уравнений
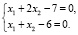
Решение системы линейных уравнений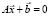 
в Scilab осуществляется по команде linsolve (A, b).
A = [1 2; 1 1]; b = [- 7; - 6].
Выполняем команду определения решения системы
x = linsolve(A,b)
и видим результат – значение вектора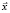 
:
x = (5, 1).
Безусловно, данная задача является одной из наиболее простых, но первоначальное знакомство с системой Scilab следует осуществлять на подобных задачах.
Рассмотрим задачу LU-разложения матрицы, т.е. представление матрицы А в виде А = C·L·U, где L и U – соответственно нижняя и верхняя треугольные матрицы, все четыре матрицы квадратные и одного порядка.
Пусть матрица А имеет вид
.
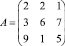A = [2 -1 5;3 2 -5;1 1 -2].
Выполним команду LU-разложения:
[L,U] = lu(A)
U =
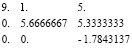
L =
Осуществим проверку:
LU = L*U
LU =
Достаточно распространенным заданием нелинейной алгебры является поиск корней полинома. В качестве примера рассмотрим полином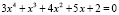 
.
Первоначально зададим вектор коэффициентов полинома (в порядке возрастания степеней):
v = [2 5 4 1 3].
Определим полином р:
p = poly(v,’x’,’c’)
p =
.
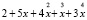Найдем корни полинома:
X = roots(p)
X = (0.3788210 + 1.2819084i, 0.3788210 – – 1.2819084i, – 0.5454877 + 0.2748651i, – 0.5454877 – 0.2748651i)
2. Дифференцирование и интегрирование функций.
В системе Scilab реализованы часто применяемые функции численного интегрирования и дифференцирования. Рассмотрим примеры некоторых заданий.
Пусть требуется вычислить значение производной функции f(x) = 2x4 – 8x3 + 8x2 –1 в точке x = 3. Для этого в Scilab реализована команда g = numdiff(fun,x).
Сначала задаем функцию f:
function f = my(x), f = 2*x^4-8*x^3 + + 8*x^2-1, endfunction.
Далее выполняем команду для вычисления производной функции в точке:
numdiff(my,3).
Получаем значение производной:
ans = 48.
Рассмотрим задачу вычисления определенного интеграла
.
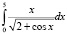Зададим подынтегральную функцию:
function y = f(x), y = x/sqrt(2 + cos(x)), endfunction.
Запишем команду вычисления определенного интеграла функции на отрезке от 0 до 5:
[I,er] = intg(0,5, f).
Значение определенного интеграла равно
I = 10.353601.
Величина ошибки при этом er = 3.264D-09.
3. Дифференциальные уравнения.
В Scilab существует возможность решения обыкновенных дифференциальных уравнений, а также дифференциальных уравнений в частных производных.
Рассмотрим решение дифференциального уравнения
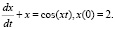
Отсюда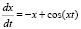 
.
Определим функцию, содержащуюся в правой части уравнения:
function yd = f(t, x), yd = – x + cos(t*x), endfunction.
Зададим начальное значение х, диапазон значений t.
x0 = 2; t0 = 0; t = 0:1:35.
Найдем решение дифференциального уравнения:
y = ode(x0, t0, t, f).
Построим график найденной функции – решения исходной задачи:
plot(t, y).
4. Обработка экспериментальных данных.
В системе Scilab реализованы сплайн-интерполяция, метод наименьших квадратов, расчет коэффициентов регрессии и другие функции, используемые для обработки результатов эксперимента.
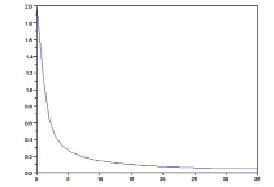
Рис. 1. Графическое решение дифференциального уравнения
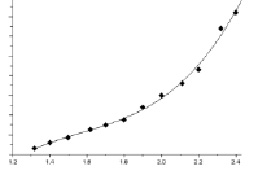
Рис. 2. Графическая интерпретация задачи
Рассмотрим решение задачи построения аналитической зависимости, наиболее точно описывающей результаты экспериментов, методом наименьших квадратов.
|
x |
1.32 |
1.40 |
1.50 |
1.62 |
1.70 |
1.80 |
1.90 |
2.00 |
2.11 |
2.20 |
2.32 |
2.40 |
|
y |
3.30 |
3.60 |
3.85 |
4.25 |
4.50 |
4.75 |
5.40 |
6.00 |
6.60 |
7.30 |
9.40 |
10.2 |
Будем искать аналитическую зависимость в виде
.
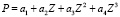Пусть a = [x; y] – матрица исходных данных, с – вектор начальных значений искомых коэффициентов функции P.
Введем функцию
.
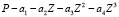function [zr] = G(c,a)
zr = a(2) – c(1) – c(2)*a(1) – c(3)*a(1)^2 – – c(4)*a(1)^3
endfunction.
Зададим значения исходных векторов Х и Y:
;
.
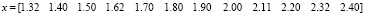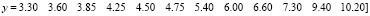Сформируем матрицу а и начальный вектор с:
а = [x;y];
c = [0;0;0;0].
Используем команду datafit для решения задачи:
[Р,err] = datafit(G,a,c)
err = 0.2486593
Р’ = (- 26.671045, 53.076245, - 31.966547, 6.7803653).
Таким образом, искомая аналитическая зависимость задается формулой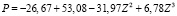 
. Построим график экспериментальных данных и в этой же системе координат график найденной аналитической зависимости:
plot2d(x,y,-4);
t = 1.32:0.01:2.40;
Ptc = Р(1) + Р(2)*t + Р(3)*t^2 + Р(4)*t^3;
plot2d(t,Ptc).
5. Задачи оптимизации
Важным направлением вычислительной математики является решение задач оптимизации. В программной системе Scilab реализована возможность поиска минимума функции одной (нескольких) переменной, решения задач линейного программирования.
Рассмотрим задачу линейного программирования.
Найти значения переменных x1, x2, x3, x4, при которых функция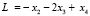 
достигает минимального значения и выполняются ограничения:
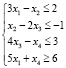
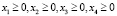
Первоначально задаем коэффициенты целевой функции:
c = [0;-1;-2;1].
Записываем матрицу коэффициентов системы ограничений и вектор свободных членов:
A = [3 -1 0 0;0 1 -2 0; 0 0 4 -1; -5 0 0 -1]; b = [2;-1;3;-6].
Задаем начальные значения x1, x2, x3, x4;
хi = [0;0;0;0].
Находим решение задачи:
[x,kl,f] = linpro(с,A,b,хi,[]).
Получаем: минимальное значение f = -2. При этом x = (1, 1, 1, 1).
Занятия по вычислительной математике охватывают огромный объем решаемых математических задач. Использование программной системы Scilab при этом упрощает изучение вычислительной математики. Первоначально студенты на практических занятиях решают типовые математические задачи на основе системы Scilab. Постепенно сложность решаемых задач увеличивается, происходит закрепление усвоенных методов. Далее каждому студенту предлагается индивидуальное задание, требующее применения разных вычислительных методов. Таким образом, практическое использование системы Scilab способствует лучшему усвоению методов решения вычислительных задач.
Заключение
Программная система Scilab является весьма полезным программным продуктом для решения разного рода вычислительных задач. Она обладает мощным функционалом для решения задач и позволяет визуально отображать результаты вычислений. Начиная с несложных заданий с использованием готовых численных методов, студенты постепенно могут переходить к написанию собственных программ, совмещающих встроенные методы и сложные программные коды. В этой связи Scilab может успешно применяться при обучении студентов решению задач вычислительной математики.