Холодная воронка – нижняя часть топки с твердым шлакоудалением, предназначенная для отвода твердого шлака в систему золошлакоудаления [2]. Холодная воронка обеспечивает организацию непрерывного сбора, перемещения и собственно отвода через нижнее отверстие в систему золоудаления золы и шлака за счет их собственного веса. Конструктивно холодная воронка – цельносварной бункер в виде перевёрнутой усеченной пирамиды. Обычно две противоположные фронтальные стенки имеют угол наклона, достаточный для свободного скольжения золы и шлака, а две другие – вертикальны. Холодная воронка с их опорной системой находится в сложном напряженном состоянии, на которое непосредственно влияют нагрузки от шлака, давления в топке и хлопка. Моделирование напряженно-деформированного состояния воронки, выбор и оптимизация её конструкции вместе с опорной системой – сложная задача для конструктора, требующая точного задания нагрузок.
В настоящее время нет достаточно полной методики расчёта нагрузок на экраны холодной воронки с учетом воздействия на экраны шлака как сыпучего тела. В связи с этим возникает проблема корректности задания усилий на экраны при проектировании холодной воронки и моделировании её напряженно-деформированного состояния. Проблема корректности задания усилий, воздействующих на экраны воронки, была решена путём дополнения нормативной методики следующим образом. Нормами [3, 4] определены следующие расчетные нагрузки: внутреннее давление, собственный вес и вес шлака, наддув или разряжение, нагрузки от неравномерного распределения температуры по сечению трубы, хлопок в топке (временная нагрузка), сейсмические нагрузки (особая нагрузка), поэтому задание этих нагрузок в модели не сложно. Так, например, в нормах нагрузок на каркасы котлов указано, что уровень заполнения шлаком холодной воронки следует принимать в 30 % её объёма для котлов производительностью до 1000 т/ч и 15 % объёма – при производительности свыше 1000 т/ч [3, 4]. Отметим, что некоторые из нагрузок (собственный вес) учитываются при моделировании в современных программных комплексах, таких как ANSYS, автоматически [1], другие (например, наддув) задаются при помощи стандартных средств программы. Но не определено распределение нагрузки от веса шлака по стенкам (экранам) холодной воронки, кроме того, не учитывается нагрузка от слоя шлака на стенки верхней (не заполненной шлаком) части воронки. На рис. 1 и 2 показаны расчётные схемы 1 и 2 с вариантами заполнения шлаком холодной воронки и воздействием его на наклонные экраны, показана половина симметричного разреза по осям фронтовых экранов.
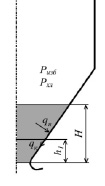
Рис. 1. Расчётная схема 1 – полное заполнение шлаком только нижней части воронки, qн и qк – соответственно, нормальное давление и касательное удельное усилие от шлака на наклонную поверхность фронтальных экранов воронки, pизб и pхл – соответственно, избыточное давление в топке и воронке и давление от хлопка топочных газов, h1 – текущее значение высоты столба шлака, H – высота верхней границы шлака в воронке
Шлак – сыпучий материал, поэтому определение нагрузок от веса шлака на стенки воронки проводили по аналогии с определением нагрузок от веса сыпучих материалов в призматических бункерах [5, С. 383–86]. Угол наклона стенок холодной воронки α выбирается с учетом угла естественного откоса шлака φ для обеспечения беспроблемного ссыпания и последующего непрерывного удаления шлака из выпускного отверстия воронки:
α = φ + c ,
где c – рекомендуемая нормативная добавка, c = 5÷10 °.
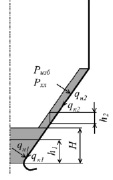
Рис. 2. Расчётная схема 2 – полное заполнение шлаком нижней части воронки и слой шлака на фронтальных экранах, qн1 и qн2 – соответственно, нормальное давление шлака на поверхность фронтальных экранов в нижней части воронки и слоя шлака в верхней части, qк1 и qк2 – соответственно, касательное удельное усилие от шлака на поверхность фронтальных экранов в нижней и верхней частях воронки, pизб и pхл – соответственно, избыточное давление в топке и воронке и давление от хлопка топочных газов, h1 и h2 – соответственно, текущее значение высоты столба шлака в нижней и высота столба шлака в верхней частях воронки, H – высота верхней границы шлака в воронке
Нормативное нормальное давление qн сыпучего тела на наклонную поверхность заполненной части бункера определяется по формуле [5, С. 384]:
qн = pнsin2α + qнcos2α ,
где горизонтальное (pн) и вертикальное (qн) нормативные давления сыпучего материала определяются по формулам:
pн = nkγh и qн = nγh ,
здесь γ – объемный вес шлака, h – высота столба шлака, принимается равной h1 или h2 для нижнего и верхнего участков нагружения (см. рис. 1 и 2), h1 изменяется от 0 до H, h2 задаётся постоянной или заданной функцией распределения шлака; k – отношение горизонтального давления к вертикальному, равное
k = pн/qн = tg2(45 – φ/2) ,
а коэффициент перегрузки n принимается равным 1,3.
Параметры сухого котельного шлака [5, С. 385]
|
Плотность, γ, кг/м3 |
Угол естественного откоса, φ, ° |
Параметр k |
Коэффициент трения f по стали |
|
600÷1000 |
35÷50 |
0,271÷0,132 |
0,4 |
Кроме нормального давления на стенки воронки действует удельное касательное усилие qк, равное
qк = (qн – pн)•sin α•cos α = = nγh•(1 – k)•sin α•cos α.
Нагрузки qн и qк рассчитываются отдельно для нижнего (индексы 1) и верхнего (индексы 2) участков нагружения (см. рис. 1 и 2).
В ходе моделирования напряженно-деформированного состояния холодной воронки задавали нормальное давление на стенки (экраны) от воздействия избыточного давления в топке, которое может быть как положительным при работе котла под наддувом, так и отрицательным при работе котла под разряжением. Задавали избыточное давление от хлопка в топке при расчете с учетом временных нагрузок или соответствующее разрежение от обратного хлопка. Для поверхностей экранов нижней части холодной воронки, заполненной шлаком, задавали нормальное давление и удельное касательное усилие, рассчитанное по вышеприведённой методике с учетом сыпучих свойств котельного шлака. При этом избыточное давление (разряжение) в топке pизб и давление от временного хлопка pхл прибавляются к вертикальному нормативному давлению от веса сыпучего материала, pизб и pхл постоянны для поверхностей экранов:
qн = nγh + pизб + pхл,
тогда
qн = qн•(k•sin2 α+ cos2α).
На поверхности экранов верхней части холодной воронки, покрытой слоем шлака заданной толщины, определяли и использовали в исходных данных моделирования нормативное нормальное давление qн и удельное касательное усилие qк. Нормальное давление от слоя шлака суммировали с избыточным давлением в топке pизб и давлением от временного хлопка pхл:
qн = nγh,
тогда
qн = qн•(k•sin2a + cos2a) + pизб + pхл ,
где t – толщина слоя шлака на поверхности экрана. Удельное касательное усилие определяли для движущегося слоя шлака как
qк = nγtf•cos α,
здесь f – коэффициент трения шлака по поверхности экрана, для неподвижного слоя как
qк = nγt•cos α.
На основе предложенной методики расчета нагрузок на экраны холодной воронки разработаны алгоритм расчета и программа – макрос для автоматизации расчета нагрузок на холодную воронку при моделировании её напряженно-деформированного состояния с помощью программного комплекса ANSYS.
МАКРОС
*DIM,hShlak,ARRAY,2 ! толщина шлака
hShlak(1) = 0.8
hShlak(2) = 0
pIzb = 0 ! избыточное давление в топке (наддув), Па
pHlop = 8730 ! давление хлопка, Па
mZola = 1400*9.81
nPere = 1.2 ! коэффициент запаса
kFi = 0.333 ! коэффициент к
alpha = 55 ! угол ската воронки
*DIM,pNorm,ARRAY,nZola (1,1)-nZola (3,1),4
*DIM,pKst, ARRAY,nZola (1,1)-nZola (3,1),4
*DO,i,1,4
*IF,i,EQ,1,OR,i,EQ,3,THEN $ k = 1 $ *ELSE $ k = 2 $ *ENDIF ! итерации по вариантам распределения золы
*IF,i,EQ,1,OR,i,EQ,2,THEN $ t = 0 $ *ELSE $ t = 1 $ *ENDIF ! итерации по нагрузкам
cy1 = ekrSt_C0+ekrSt_cy(nekrSt-1)+ekrSt_cy(nekrSt)
cy2 = cy1+ekrSt_cy(nZola (1,1))
*DO,j,1,nZola (1,1)-nZola (3,1)
*IF,j,GT,nZola (1,k)-nZola (2,k),THEN $ m=1 $ *ELSE $ m=0 $ *ENDIF
! итерации по 2-м зонам заполнения шлаком экрана (2-я – это шлак на стенке до верха ХВ)
jhZola = 0.5*(cy2-cy1)+hZola(k)-cy2
jhZola = jhZola – m*(jhZola – hShlak(k)/cos(PI*alpha/180))
pNorm(j,i) = (nPere*mZola*jhZola+(1-m)*pIzb+t*(1-m)*pHlop)*(kFi*sin(PI*alpha/180)*sin(PI*alpha/180)+cos(PI*alpha/180)*cos(PI*alpha/180))+m*pIzb+t*m*pHlop
pKst(j,i) = (nPere*mZola*jhZola+(1-m)*pIzb+t*(1-m)*pHlop)*(1-kFi)*sin(PI*alpha/180)*cos(PI*alpha/180)+m*pIzb+t*m*pHlop
*IF,k,EQ,2,AND,m,EQ,1,THEN
pKst(j,i) = 0
*ENDIF
cy1 = cy2
cy2 = cy2 + ekrSt_cy(nZola (1,k)-j)
*ENDDO
*ENDDO
В Макросе задаётся распределение нормального и касательного (массивы pNorm и pKst соответственно) давления шлака, избыточного давления и давления хлопка по высоте экрана по участкам. Формируется две комбинации нагрузок: вес золы и избыточное давление для 2 вариантов распределения золы (первый и второй индексы массивов) и вес золы, избыточное давление и давление хлопка для 2 вариантов распределения золы (третий и четвёртый индексы массивов). В нашем случае воронка разбита на участки длиной от 150 до 300 мм, отметки участков содержатся в массиве nZola, а длины участков – в массиве ekrSt_cy. В макросе для каждого участка определяются координаты верхней и нижней точек (cy1, cy2) и высота шлакового столба (jhZola) после чего вычисляются значения нормального и касательного давления по участкам. Вычисленные значения нагрузок задаются далее на конечные элементы участков (должны быть выбраны предварительно) следующим образом:
sfe,all,1,PRES, ,pNorm(j,i)
Касательные нагрузки задаются с помощью поверхностных элементов командами:
еsurf
sfe,all,3,PRES, ,pKst(j,i)
Предложенная методика расчета нагрузок на экраны холодной воронки апробирована при моделировании напряженно-деформированного состояния холодной воронки парового котла мощностью 600 МВт и паропроизводительностью 1710 тонн пара в час.
Выводы
1. Предложена методика расчета нагрузок на экраны холодной воронки, позволяющая учитывать распределение шлака на наклонных стенках воронки и его силовое воздействие на экраны, повысить точность моделирования напряженно-деформированного состояния экранов холодной воронки с их опорной системой и может служить одним из инструментов оптимизации конструкции опорной системы.
2. Предложенная методика расчета нагрузок на экраны холодной воронки позволяет учитывать воздействие на экраны от шлака как сыпучего тела с учетом его физико-механических характеристик, угла наклона стенок холодной воронки α и распределения шлака в воронке.
3. Разработанный на основе предложенной методики макрос для программного комплекса ANSYS позволяет автоматизировать расчет нагрузок на холодную воронку при моделировании её напряженно-деформированного состояния.



