Для повышения быстродействия всей вычислительной системы усложняются структура и архитектура современных микросхем полупроводниковой памяти. Микросхемы памяти DDR и QDR типов обеспечивают считывание или запись по одной команде пакетов данных длиной до 8 слов. Для выполнения тестового диагностирования быстродействующих микросхем памяти на этапе изготовления целесообразно применять устройства тестового диагностирования (УТД), имеющие мультипроцессорную структуру, содержащую несколько групп формирователей кода адреса, данных и компараторов.
Значительный вклад в формирование теоретических и практических основ диагностики полупроводниковых элементов памяти с привлечением тестовых методов внесли ученые А.А. Иванюк, В.И. Хаханов, В.Н. Ярмолик, D.S. Suk, S.M. Reddy, A.J. Van de Goor, Y.Y. Zorian и другие [8, 12, 13]. Однако в большинстве литературных источников приведены описания алгоритмов и свойства тестов, а принципы проектирования тестов и применяемые при этом средства излагаются недостаточно подробно [5]. Разработка программ тестов диагностирования быстродействующей оперативной памяти сопряжена с высокой трудоемкостью и связана со значительными затратами времени и материальных средств, поэтому требуется создание новых методов и средств, уменьшающих продолжительность проектирования тестов [1–3].
Целью данной статьи является разработка методов и средств автоматизированного проектирования тестов диагностирования быстродействующих запоминающих устройств.
Теоретические основы построения модели диагностируемой памяти и устройства диагностирования
Для проектирования алгоритмов и программ тестов быстродействующих запоминающих устройств предлагается программная модель объекта и устройства диагностирования, которая позволит сократить трудоемкость проектных операций [4]. Структурная схема взаимодействующих объекта и устройства диагностирования (рис. 1) содержит устройство управления (УУ), матрицу запоминающих ячеек и операционные процессоры (ОП).
В качестве объекта диагностирования в модели используется квадратная матрица запоминающих ячеек размером 16×16, при этом обеспечивается удобный вывод их состояния на экран монитора. Все запоминающие ячейки нумеруются цифрами, начиная от 0 до 255. Запись и считывание данных в ячейки обеспечивают операционные процессоры, число которых обычно кратно 2.
Последовательность формируемых тестов определяется УУ, которое может находиться в одном из конечного числа состояний, которое определяется номером текущей команды в программе. В соответствии с текущим состоянием УУ каждый ОП может записывать новые данные в выбранную ячейку и перемещаться независимо друг от друга влево или вправо либо остаться на месте. Для сканирования ячеек памяти при помощи нескольких ОП нужно определить их начальное состояние и набор микроопераций для изменения шага приращения их кода адреса.
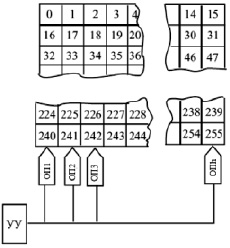
Рис. 1. Структура модели объекта и устройства диагностирования
Предлагаемая математическая модель задается пятеркой компонентов:
M = <Q, q0, S, рr, d>,
где Q – множество состояний УУ; q0 – начальное состояние УУ; S – множество символов алфавита; рr – величина приращения координаты r-го ОП; d – функция переходов, которая отображает некоторое подмножество множества Q×(Sr×pr), то есть для заданного состояния УУ и символов, обозреваемых ОП, выдает новое состояние, новые символы и приращения координат ОП.
Пусть
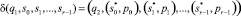
и УУ находится в состоянии q1, а i-й ОП обозревает символ si, тогда УУ перейдет в состояние q2, заменит символы si на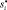 
и все ОП изменят свои позиции на pi.
Сформулированные ниже теоремы доказывают необходимость и достаточность набора микроопераций для разработки программ наиболее распространенных тестов диагностирования полупроводниковой памяти.
Теорема 1. Для обращения ко всем ячейкам памяти запоминающего устройства емкостью n = 2m бит, где m – целое положительное число больше 3, с увеличением кода адреса колонок устройством, имеющим h = 2k операционных процессоров и двухкоординатную систему адресации, где k ≤ m, достаточно следующего набора микроопераций формирования кода адреса:
m1 = {x := gx, y := gy, x := x + 1, ..., x := x + 2k, y := y + 1, y := y + 1*},
где gx – начальный адрес по координате Х; gy – начальный адрес по координате Y; символ * означает наличие переноса из координаты Х.
Доказательство. Рассмотрим случай, когда k = 2, m = 8, то есть память, имеющую 256 ячеек и h = 22 = 4 операционных процессора, формирующих коды адреса и обеспечивающих выбор ячеек памяти для записи или считывания. Для установки ОП в исходное состояние используем следующий набор микроопераций, представленный в виде матрицы, строки которой определяют положения ОП: первая для ОР0, вторая – ОП1, третья – ОП2, четвертая – ОП3:
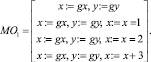
Для выбора всех остальных смежных ячеек с увеличением кода адреса колонок применим следующий набор микроопераций:
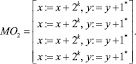
Так как емкость микросхемы памяти в модели n = 256 бит и кратна числу ОП h = 4, поэтому, циклически повторяя набор микроопераций MO2, можно выбрать все ячейки памяти для данного направления сканирования. Матрицы MO1 и MO2 содержат только микрооперации, приведенные в теореме 1, что подтверждает ее справедливость. Если емкость памяти и число операционных процессоров удовлетворяет условиям теоремы 1, то для любой допустимой их комбинации можно составить наборы микроопераций, аналогичные наборам MO1 и MO2 для выбора всех ячеек с возрастанием кода адреса колонок.
Теорема 2. Для обращения ко всем ячейкам памяти емкостью n = 2m бит, где m – целое положительное число больше 3, с увеличением кода адреса рядов устройством, имеющим h = 2k операционных процессоров и двухкоординатную систему адресации, где k ≤ m, достаточно следующего набора микроопераций для формирования кода адреса:
m2 = {x := gx, y := gy, y := y + 1, y := y + 2, ..., y := y + 2k, x := x + 1}.
Теорема 3. Для обращения ко всем ячейкам памяти емкостью n = 2m бит, где m – целое положительное число больше 3, с уменьшением кода адреса колонок устройством, имеющим h = 2k операционных процессоров и двухкоординатную систему адресации, где k ≤ m, достаточно следующего набора микроопераций для формирования кода адреса:
m3 = {x := nx, y := ny, x := x – 1, x := x – 2, ..., x := x – 2k, y := y – 1*}.
Здесь символ * означает наличие займа из координаты Х.
Теорема 4. Для обращения ко всем ячейкам памяти емкостью n = 2m бит, где m – целое положительное число больше 3, с уменьшением кода адреса рядов устройством, имеющим h = 2k операционных процессоров и двухкоординатную систему адресации, где k ≤ m, достаточно следующего набора микроопераций для формирования кода адреса:
m4 = {x := nx, y := ny, y := y – 1, y := y – 2, ..., y := y – 2k, x := x – 1}.
Аналогично приведенному доказательству теоремы 1 можно доказать справедливость теорем 2, 3 и 4. Для разработки программ тестов необходимо учитывать следствия, которые вытекают из данных теорем.
Следствие 1. Для циклического выполнения фрагментов программ тестов, функционирующих согласно условиям и указаниям, приведенным в теоремах 1 и 2, необходимо использовать флаг условного перехода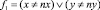 
, который формируется (h – 1)-м операционным процессором.
Следствие 2. Для циклического выполнения фрагментов программ тестов, функционирующих согласно условиям и указаниям, приведенным в теоремах 3 и 4, необходимо использовать флаг условного перехода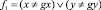 
, который формируется (h – 1)-м операционным процессором.
Применение матриц инциденций графов адресных переходов для автоматизации распараллеливания микроопераций в алгоритмах тестов
Значительного повышения быстродействия диагностических устройств можно достичь за счет распараллеливания микроопераций формирования кодов адреса, данных и обработки считанных реакций устройством диагностирования, имеющим мультипроцессорную структуру [1, 3]. Однако применение мультипроцессорной структуры диагностических устройств увеличивает сложность проектирования алгоритмов и программ тестов, так как необходимо управлять одновременной работой нескольких ОП.
Для определения элементов матриц инциденций используются следующие обозначения: а i,j = 1, если ребро j уходит из вершины i; a i,j = –1, если ребро j подходит к вершине i или в вершине i имеется петля; ai,j = 0, если ребро j не имеет общей точки с вершиной i.
Наличие петель в преобразуемых графах соответствует операциям многократного обращения к одной и той же ячейке памяти, что характерно для большинства применяемых тестов семейства march.
Пусть задана матрица инциденций М размером n×m элементов:
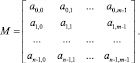
Требуется разбить её на k матриц размером (n×m/k) каждая. Для решения данной задачи выполним следующие преобразования:
(*)
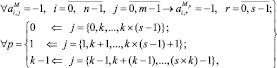где s = m/k – число столбцов в матрицах M0, M1, ..., Mk–1.
Таким образом, каждый j-й столбец матрицы М преобразуется в r-й столбец матрицы Мp. Дополним полученные матрицы единичными элементами:
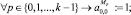(2)
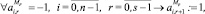
кроме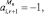 
причем (r + 1) не больше, чем (s – 1).
Например, пусть задана матрица инциденций, которая имеет вид: A = (aij)mn, содержит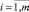 
строк и 
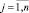столбцов. После выполнения преобразований, приведенных выше, получаем матрицы инциденций, которые отображают работу отдельных ОП:
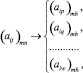
где aip, aiq, ..., aiw – элементы вновь сформированных матриц; h = n/l – число столбцов в данных матрицах.
Число сформированных матриц равно количеству ОП. На основании полученных матриц определяются микрооперации смены позиций для каждого ОП.
Рассмотренные выше матричные преобразования реализованы в программе Transfor.exe, осуществляющей разбиение и объединение матриц инциденций направленных графов [6, 7, 9]. Главное меню программы Transfor.exe приведено на рис. 2. Опция «Direct Transformation» обеспечивает объединение нескольких матриц в одну матрицу, а опция «Inverse Transformation» обеспечивает разбиение одной матрицы на несколько матриц.
Для отображения операций диагностирования запоминающих устройств используется операторная форма записи алгоритмов [3]. Операцию обращения для записи нуля в ячейку памяти с адресом (а) отображает оператор V(a), записи единицы – W(а), считывания данных – R(а). Операции записи единиц во все ячейки при возрастании кода адреса записываются в виде последовательности операторов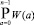 
. Здесь символ Р определяет последовательность выполняемых операций, нижний индекс определяет начальный адрес ячейки памяти, а верхний индекс – конечный адрес запоминающих ячеек.
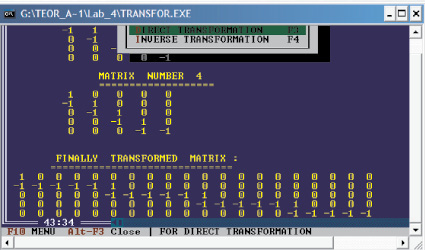
Рис. 2. Окно программы Transfor.exe при объединении матриц
Рассмотрим пример преобразования матрицы инциденций для теста march_Y, алгоритм которого в операторном виде имеет вид
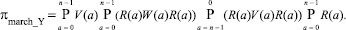
Граф адресных переходов сканирования ячеек памяти данным тестом с увеличением кода адреса приведен на рис. 3.
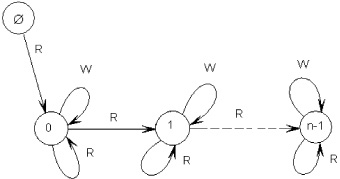
Рис. 3. Граф теста march_Y при увеличении кода адреса
Матрица инциденций данного теста для 8 ячеек памяти приведена ниже.
Для распараллеливания операций данного теста при функционировании устройства, имеющего четыре ОП, выполним преобразования данной матрицы при помощи программы Transfor и получаем 4 матрицы, которые отображают адресные переходы четырех ОП:
На основании анализа полученных матриц можно определить микрооперации изменения кода адреса для выполнения теста march_Y устройством диагностирования, имеющим 4 ОП.
Для разработки алгоритмов и программ тестов быстродействующих запоминающих устройств, а также для анализа выполняемых операций разработана интерпретирующая система Prover, в которой предусмотрены три режима работы: автоматический, пошаговый и графический [10, 11]. При достижении команды останова на экран выводится сообщение о корректности или об ошибках в программе теста.
Выводы
Разработанную программную модель взаимодействующих микросхемы памяти и устройства диагностирования можно использовать в конструкторских, научно-производственных объединениях и высших учебных заведениях для разработки новых диагностических систем. Предложенный метод распараллеливания микроопераций тестов полупроводниковой памяти, основанный на преобразованиях матриц инциденций графов адресных переходов, повышает производительность труда программистов в 3,8 раза при применении двух операционных процессоров, и в 4,2 раза при четырех параллельно работающих операционных процессорах.
Работа выполнена при финансовой поддержке гранта РФФИ (проект 16-08-00393).