Если говорить о специальностях и направлениях [1, 2] квалификационных работ, о которых в статье идет речь, то это педагогика, психология, экономика, менеджмент, а также технические науки. Имеются в виду будущие бакалавры, магистры, специалисты, а также аспиранты, докторанты и соискатели ученых степеней. В чем особенность, на наш взгляд, научных результатов в указанных выше областях? Для сравнения рассмотрим, во-первых, физико-математические и естественные науки, а во-вторых, чисто гуманитарные науки. В первых оценка результатов, как правило, не может быть субъективной, поэтому такие оценки обычно количественные, и они базируются почти исключительно на математических методах. Во вторых оценка результатов чаще всего не может быть объективной, поэтому такие оценки обычно качественные и они базируются почти исключительно на так называемых правдоподобных рассуждениях [5] в смысле Пойа.
Наши же области [2] занимают промежуточное положение между первыми и вторыми. Здесь полностью нельзя исключить ни объективности, ни субъективности. В частности, технические науки не могут не использовать эвристику, а следовательно, и правдоподобные рассуждения. Эвристика [1] точной наукой не является. А математика и физика служат обычно постфактум для точного описания уже имеющихся результатов деятельности творца (инженера, экономиста, менеджера, педагога, психолога). Если имеющиеся количественные показатели не дают возможности обосновать полученный результат, то исследователь может разработать новые показатели и целевые функции. Причем разработать их надо так, чтобы опытным (эмпирическим) путем можно было количественно показать, что полученный результат и именно он действительно способствует улучшению этих показателей. А это эвристическая задача.
Вот небольшой пример. Обычный путь при проведении педагогического эксперимента по обоснованию новой педагогической технологии – это считать средние баллы в контрольной и экспериментальной группах. Рассматриваемых в ходе эксперимента обучаемых делят на две группы: экспериментальную (где эта новая технология применялась) и контрольную (где она не применялось). И эти баллы ставят студентам сам изобретатель новой технологии или его ближайшие коллеги! Никакие математические методы не сделают обоснование такого результата объективным. Для исключения субъективного фактора обычно в этих группах не только работают несколько преподавателей, но и для выяснения мнения обучаемых или преподавателей по какому-либо вопросу, как правило, проводят анонимное анкетирование.
Можно планировать анонимные анкетирования обучаемых по таким, например, вопросам: «Сколько процентов учебного материала (по времени работы с ним) было Вами усвоено?»; «Сколько процентов учебного материала будет Вам полезно в будущей профессиональной деятельности?»; «Сколько процентов учебного материала были Вам интересны, познавательны?» Один из авторов данной статьи (Р.Р. Фокин) именно так и спланировал педагогический эксперимент [2] в своей докторской диссертации.
При анкетировании рекомендуется не использовать вопросы с открытой, т.е. с нерегламентированной формой ответа [1, 7], например: «Что Вам понравилось и не понравилось в прослушанном учебном курсе и почему?» Обработку ответов на такие вопросы трудно формализовать, а при отсутствии формализации мы целиком полагаемся на субъективность человека, обрабатывающего соответствующую информацию.
Для исключения субъективности обычно рекомендуется использовать вопросы с закрытой, т.е. с регламентированной формой ответа, например: «Понравился ли Вам прослушанный курс? Выберите ответ из вариантов: 1 – да; 2 – нет; 3 – не могу решить» или «На какую оценку 1, 2, 3, 4 или 5 Вы сами оценили бы свои знания по прослушанному курсу?» или «Сколько приблизительно процентов (0–100) времени, потраченного Вами для изучения материалов курса, заняла у Вас неинтересная, рутинная работа?»
В первых двух случаях ответы – это целые числа из небольшого множества {1...3} или {1...5}, т.е. мы имеем дискретные случайные величины. В третьем случае ответ – это действительное число из отрезка [0, 100], большинство будет писать целые числа кратные 5, например, 45, несколько испытуемых выберут целые числа не кратные 5, например, 37, в принципе отдельные оригиналы могут написать, например, 41,738, т.е. мы имеем непрерывную ограниченную случайную величину, распределение которой не является равномерным, не является нормальным и больше о нем сказать нечего.
Гипотеза – это утверждение, истинность которого следует обосновать. Гипотеза диссертационного исследования [7, 8] обычно имеет следующую структуру: если применять предложенную новацию, то качество каких-то процессов (социальных, личностных, педагогических, технических, экономических) улучшится. Такую гипотезу обычно невозможно полностью обосновать теоретически только точными рассуждениями, необходимы также правдоподобные рассуждения и эксперимент с математически корректной обработкой полученных данных. Именно разработанные исследователем показатели и целевые функции, о которых говорилось выше, должны фигурировать в гипотезе диссертационного исследования.
В наших работах для обоснования внедрения некоторой педагогической новации – сервисов обучения (СО) информационным технологиям (ИТ) студентов мы сформулировали гипотезу следующим образом: в результате внедрения предлагаемых СО может повыситься качество обучения студентов ИТ в результате: повышения доли усвоенных и освоенных ими знаний и навыков; повышения доли полезных в их будущей профессиональной деятельности знаний и навыков; повышения доли полезных им в учебе знаний и навыков; повышения доли полезных им в быту знаний и навыков; повышения доли интересных для них знаний и навыков. Имеются в виду доли знаний и навыков, относящихся к дисциплинам, связанным с ИТ.
В педагогических исследованиях принято качественно и количественно обосновывать гипотезу исследования. Качественно обосновывается возможность практического применения предложенного в данном исследовании, приводятся рабочие программы курсов, учебные планы и т.п. На основе полученных в ходе эксперимента численных данных количественно обосновывается то, что практически что-то улучшилось. Пусть мы имеем выборку {x1, x2, ..., xn} для экспериментальной группы и {y1, y2, ..., ym} – для контрольной.
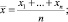
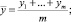(1)
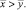
Допустим, по результатам эксперимента одно среднее получилось большим, чем другое среднее – формула (1). Есть основания говорить, что экспериментальная методика лучше классической или дело просто в случайности? Может быть, это просто случайно так получилось, а совсем не потому, что к генеральной случайной величине X применялась разработанная новация, а к Y – нет. Во многих дипломных работах и диссертациях обучаемые этот вопрос себе не задают. Делать выводы на основе статистических данных следует очень осторожно. В книге ученого-статистика В. Боровикова [3] на стр. 120 приводится следующий шуточный пример. Собранные за много лет данные говорят о том, что чем больше пожарных участвует в тушении пожара, тем больше, как правило, оказывается ущерб от пожара. Следовательно, только на основе этих статистических данных можно сделать вывод: для минимизации ущерба целесообразнее пожарных вообще не вызывать.
Для обоснования того, что одно среднее больше другого не случайно, некоторые исследователи используют t-критерий Стьюдента, а соответствующие статистические пакеты прикладных программ (ППП) позволяют при этом вычислить уровень значимости u, с которым гипотезу о равенстве средних можно отвергнуть. Обычно для исследований в областях педагогики и психологии считается приемлемым u ≤ 0,05. Вероятность ошибки первого рода (уровень значимости) u означает, что если мы отвергли гипотезу, а она на самом деле была верна, то вероятность такой ошибки не превосходит u. Следовательно, то, что одно среднее получилось большим, чем другое среднее – закономерно.
Если X и Y – независимы, то {x1, x2, …} и {y1, y2, …} – независимые выборки. Например, экспериментальная и контрольная группы студентов занимаются независимо друг от друга. X – какой-то показатель среднестатистического студента экспериментальной группы. Y – тот же показатель среднестатистического студента контрольной группы. Если X и Y – зависимы, то {x1, x2, …} и {y1, y2, …} – зависимые выборки. Например, речь идет об одной и той же группе студентов (n = m). Ко всем студентам группы применили некоторую новацию. Y – какой-то показатель среднестатистического студента группы до применения новации, X – тот же показатель того же студента после применения новации. Существуют разновидности t-критерия Стьюдента для независимых выборок и для зависимых выборок. При независимых выборках t-критерий Стьюдента требует равенства дисперсий (DX = DY). Для случая DX ≠ DY существует особый критерий, аналогичный t-критерию Стьюдента.
В случае DX ≠ DY актуально также применение однофакторного дисперсионного анализа и F-критерия. В этом случае, говоря, например, о полезности некоторых педагогических новаций, являющихся предметом научного исследования, можно не просто рассматривать фактор принадлежности-непринадлежности студента к экспериментальной группе, а дозировать эти новации по отношению к различным группам студентов: контрольная группа (новации не применялись); первая экспериментальная группа (новации применялись более года); вторая экспериментальная группа (новации применялись более 2 лет) и так далее.
Но в условиях соответствующих теорем [6] о разновидностях t-критерия Стьюдента всегда требуется нормальность X и Y. В большинстве работ, где используется t-критерий Стьюдента [4], эта нормальность не обосновывается никак. Если X и Y – дискретны (какие-то баллы, например), то их нормальность обосновать невозможно – это основы теории вероятностей. В некоторых учебных пособиях, разработанных профессиональными педагогами и психологами (но не математиками), стало «классическим», например, применение к баллам от 1 до 5, т.е. к дискретным случайным величинам t-критерия Стьюдента. Почему? В ответ иногда можно услышать, что «они стремятся к нормальным».
На законные вопросы «Что стремится?» и «Как стремится?» ответ дает центральная предельная теорема: Пусть {x1, x2, ..., xn, ...} – последовательность взаимно независимых одинаково распределенных случайных величин, имеющих математическое ожидание p и дисперсию q2, тогда случайная величина an = (x1 + x2 + ... + xn)/n асимптотически нормальна с математическим ожиданием pn = p и дисперсией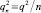 
. Согласно определению асимптотической нормальности, величина bn = (an – pn)/qn слабо сходится к стандартному нормальному распределению N(0, 1). При больших n «близка» к нормальной величина bn, но это одно число, следовательно, мы получили выборку объемом 1, а изначально у нас была выборка {x1, x2, ..., xn} объемом n.
Если генеральные случайные величины X и Y непрерывны, то обосновать их близость к нормальному распределению можно. Если, конечно, они действительно к нему близки. Для этого, например, к ним можно применить специальный критерий Колмогорова – Смирнова, который реализован во многих статистических ППП. В случае обоснования близости X и Y к нормальному распределению их практически в ходе эксперимента можно считать нормальными.
А если X и Y – дискретны (случай 1) или X и Y – непрерывны, но их практически нельзя считать нормальными (случай 2), то что делать тогда? Тогда нужно применять так называемые непараметрические (свободные от распределения) статистические критерии проверки гипотез, среди которых наиболее известны семейства критериев хи-квадрат, семейства критериев Колмогорова – Смирнова, U-тест Манна – Уитни, Мозеса, Уальда – Вольфовица, тест Уилкоксона, знаковый тест и другие. Некоторые из них работают с независимыми выборками, другие – с зависимыми. В случае 1 можно порекомендовать, например, семейства критериев хи-квадрат, в случае 2 – семейства критериев Колмогорова – Смирнова. Можно применять любые из указанных здесь критериев, предварительно изучив условия их применимости и проверив выполнение этих условий.
В случае независимого обучения экспериментальной и контрольной групп студентов статистические ППП позволяют вычислить уровень значимости, с которым гипотезу о равенстве функций распределения X и Y можно отвергнуть. Их вероятностные распределения разные, следовательно, то, что одно среднее получилось большим, чем другое среднее – закономерно. А в какой группе среднестатистический студент лучше? В экспериментальной, поскольку там среднее больше – формула (1). В случае приведенной выше нашей гипотезы о полезности применения СО студентов ИТ, доли, выраженные в процентах – это непрерывные случайные величины. Поэтому для подсчета уровня значимости u мы используем разновидность критерия Колмогорова – Смирнова (для двух независимых выборок). Его часто называют [6, 7] критерием Смирнова. Он состоит в следующем.
(2)
Имеются две непрерывных случайных величины X и Y. В ходе проверки мы хотим отвергнуть гипотезу о том, что равны их функции распределения (Fx = Fy), следовательно, что одинаковы их вероятностные распределения. Пусть у нас имеются соответствующие выборки {x1 ... xn} и {y1 ... ym}. Пусть x* и y* – дискретные эмпирические случайные величины, построенные по соответствующим выборкам – формула (2). Здесь a1 < a2 < … < ak – это те же x1, x2, …, xn, но без повторений, p1, p2, …, pk – это их относительные частоты; b1 < b2 < … < bl – это те же y1, y2, …, ym, но без повторений, q1, q2, …, ql – это их относительные частоты. Пусть Fx*(t) и Fy*(t) – их выборочные функции распределения.
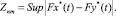(3)
Далее по формуле (3) вычисляется статистика Znm. Вероятностное распределение Znm хорошо изучено. Зная Znm, n, m, можно найти [8] искомый уровень значимости u, при котором отвергается гипотеза.
Критерии хи-квадрат работают с дискретными случайными величинами и требуют небольшого объема вычислений. Критерии Колмогорова – Смирнова, U-тест Манна – Уитни, Мозеса, Уальда – Вольфовица, тест Уилкоксона, знаковый тест работают со случайными величинами произвольного распределения, но их применение требует вычислительной работы значительно большего объема. Особо чувствительными являются методы Колмогорова – Смирнова, но они требует достаточно большого объема вычислений, которые без компьютера провести практически невозможно.
Теперь несколько слов о компьютерной реализации упомянутых выше статистических критериев проверки гипотез. Хи-квадрат и t-критерий Стьюдента могут быть достаточно просто реализованы в среде электронных таблиц, например в Microsoft Excel, без применения программирования. Для критериев U-тест Манна – Уитни, Мозеса, Уальда – Вольфовица, тест Уилкоксона, знаковый тест без простейших приемов программирования уже не обойтись. Методы Колмогорова – Смирнова и другие современные статистические методы могут быть реализованы с помощью достаточно сложных методов программирования, например, с помощью VBA в среде Microsoft Excel или без программирования с помощью профессиональных статистических ППП, содержащих почти все известные статистические методы. Среди подобных пакетов для Microsoft Windows наиболее известны IBM SPSS-Statistica и Statgraphics. Поскольку российские вузы в настоящее время используют, как правило, лицензионное программное обеспечение, то следует заметить, что эти статистические пакеты значительно дороже Microsoft Windows и Microsoft Office. При этом если Microsoft предоставляет значительные скидки для учебных заведений на свое программное обеспечение, то производители профессиональных математических пакетов – это часто фирмы, не дающие льготных цен вузам, за исключением фирмы IBM, которая в настоящее время является правообладателем многих таких профессиональных пакетов прикладных программ и предоставляет значительные скидки вузам.