Как известно, усвоение знаний, приобретение умений, развитие мышления учащегося достигается путем сложного сочетания таких различных факторов, как: логика изложения материала в учебнике, воздействие на школьника, объяснение учителя. А также таких психологических черт учащегося, как его способности, память, общее развитие, быстрота усвоения и ориентировка в материале и т.д.
И для того, чтобы глубже проанализировать процесс формирования и развития мышления учащегося в процессе обучения, обнаружить его сильные и слабые стороны, развить первые и, по возможности, исключить вторые, мы должны постараться выделить в обучении роль и влияние на его успешность каждого из перечисленных выше факторов или, по крайней мере, важнейших из них.
Несомненно, наиболее важной стороной в обучении математике являются строго логическое изложение предмета, его теорий, теорем и их доказательств и развитие логического мышления школьника.
Первая проблема у нас не решена. Почему не удается эффективно формировать мыслительную деятельность учащихся при обучении математике? На наш взгляд, учитель до сих пор мало знает о мышлении вообще, о процессе формирования мыслительной деятельности учащихся, а потому и не умеет эффективно этим пользоваться при обучении математике.
Итак, где мы можем искать те факторы, которые столь активно влияют на процесс формирования мышления? На наш взгляд, резервы надо искать в обращении к закономерностям психологии и педагогики, которые характеризуют процессы мышления в обучении. Мышление человека должно подчиняться особым закономерностям, которые изучает психология, и обучение учащихся математике в этом случае выступает как двойственный процесс. С одной стороны, надо учесть психологические особенности обучающегося, а с другой – учесть специфику математики. Поэтому этот процесс должен учитывать как факторы, связанные с математикой (теоремы, понятия, доказательства и т.д.), так и факторы, связанные с человеком (психолого-педагогические, влияющие на него). Отсюда вывод: учитель, заинтересованное лицо в успешности обучения, не может игнорировать всех этих факторов, так как от них зависит продуктивность мышления учащихся.
В этой «двойственности» процесса обучения в один узел связываются вопросы математики как науки и вопросы психики человека, и в этом состоит вся трудность проблем методики обучения математике. В ежедневном обучении учитель обычно видит перед собой не столько живого учащегося, с его знаниями и памятью, интересами и возможностями, со всеми его достоинствами и недостатками, желаниями и настроениями, радостями и переживаниями, сколько некую интеллектуальную машину, готовую в любую минуту к усвоению знаний. В действительности же эти психические факторы, чуждые математике, на самом деле решающим образом влияют на ее усвоение. Не учитывать их значило бы при решении вопросов обучения исключить из рассмотрения того самого человека, которого мы обучаем. Продуктивность мышления учащегося зависит от того, как человек относится к учению, интересует оно его или нет, понимает он его необходимость или не понимает [4]. Знания, получаемые с охотой, скорей усваиваются и лучше запоминаются, чем знания, насильно «втиснутые» в сознание.
Однако в методической науке не так много способов, благодаря которым можно пробудить интерес к познанию. И детей, интересующихся математикой, не так много. Чтобы их было больше, надо сделать так, чтобы математические задачи учащимся хотелось читать и решать. Кого могут привлечь традиционные скучные: «Пешеход вышел из пункта А в пункт В…»; «Две трубы наполняют бассейн…»; «Найди», «Вычисли» и пр. Более результативным будет учебный процесс, когда школьник глубоко переживает события, изложенные в тексте нового материала. Эмоционально поданный материал лучше усваивается и воспроизводится. Из-за недостаточно обдуманной организации учебного процесса теряется интерес к учению. Следует обратить внимание и на то, насколько материал является посильным. Новый материал должен быть подан таким образом, чтобы ученик «услышал» этот материал, обязательно «увидел» формулу. Для этого необходимо обеспечить интерес к усвоению математического материала с помощью умело и разумно использованного приема так, чтобы ученик не уклонялся от достижения поставленной цели, не забывал о средствах ее достижения.
Специальным подбором целой серии интересных для учащихся приемов, задач, вопросов и особой их постановкой (как для письменного, так и для устного решения) учителя математики будят творческую мысль учащихся.
Приведем отдельные примеры:
1. Всегда ли верно: а : а = 1; х2 > х; 2а > а?
2. Может ли оказаться, что а больше 5а?
3. Чем является единица в выражениях 5а + 1, 1•а + 5?
4. Делится ли многочлен
а2 – с2 + b(2а + b)
на а + b – с?
5. Дано а > 0 и b < 0. Какое из них больше и на сколько?
6. а) Чему равна разность |а| – а?
б) Чему равна сумма а + |а|?
в) Чему равна дробь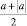 
? И т.п.
Ответы на вопросы, решение примеров и задач всегда вызывают интерес у учащихся. После удачного ответа учащиеся испытывают моральное удовлетворение, у них появляется желание работать лучше, а это и является одним из существенных моментов, способствующих привитию интереса к предмету.
Как показывает опыт работы авторов в качестве преподавателей, процесс усвоения новых знаний учащимися далеко не так гладок, как это может показаться. Новые знания не просто добавляются к старым. Новые знания должны войти в тесный и органический контакт с уже освоенными.
Правильного понимания смысла математических понятий школьник может достигнуть только после тщательных разъяснений учителя и самостоятельного выполнения достаточного количества упражнений и решения задач.
Несомненно, важнейшим фактором успеха в обучении является интерес ученика к математике. Следовательно, и учебник, и учебное объяснение должны быть интересными. Хорошо известно, что интересный материал усваивается почти без усилий и хорошо запоминается, а скучный усваивается с трудом и быстро забывается. Интерес повышает уровень логического мышления, позволяя ученику решать задачи определенной трудности и усваивать такой материал, который иначе он бы не осилил. Сейчас организация интересного обучения всецело зависит от мастерства отдельного учителя. Хотя по насыщенности программ это далеко не всегда удается. Интерес учеников к учебе надо рассматривать как один из самых мощных факторов обучения. Мы должны осознать, что интерес не забава, что интересное обучение – это не уступка ленивому ученику.
В создании интереса к математике большую роль играют задачи. Но задачи, включенные в учебник, в основном очень сухи. Цель авторов учебника – включить все задачи, необходимые для формального усвоения материала темы. Между тем важно, чтобы задачник был увлекательным. Он должен, наряду с обычным набором необходимых задач, содержать задачи с интересным содержанием, задачи, которые хватают за живое, которые не бросишь, не решив, возможны задачи-парадоксы и т.д. Ученик с захватывающим интересом будет выполнять даже самый скучный арифметический подсчет, если он служит проверкой правильности задуманного им решения интересной задачи. Все то, что способно приковать к себе внимание учащегося и пробудить его мысль (различные неожиданные и нешаблонные задачи, анализы всевозможных парадоксов и софизмов), должно найти себе место в школьном обучении. Однако сейчас это мало практикуется в учебном процессе. Такие задачи допускаются лишь в «книгах для чтения». Не нужно бояться, что интересные задачи снизят уровень обучения учащихся. Наоборот, они повысят его. Без преувеличения можно сказать, что интерес – лучшее проявление знаний в сознании человека.
Как известно, всякая работа выполняется в двух планах: внешние действия – видимые, и внутренние, не доступные постороннему наблюдателю. Внутренняя работа обычно не осознается и самим выполняющим ее человеком, но именно внутренний план является наиболее важным, так как выполняемой работой руководит мозг человека, его сознание. И поэтому от правильно организованной умственной работы зависит усвоение знаний.
Контроль над ходом «внутренней мысли» учащегося позволит учителю установить сильные и слабые стороны мышления ученика, следовательно, получить возможность сделать конкретные выводы о том, как направить мышление учащегося на правильный путь. Поэтому, чтобы научить учащихся решать математические задачи, очень важно установить, как ученик думает, решая задачу. Как учащийся воспринял условие задачи? Что он собирается делать? Каковы последовательные этапы? Каковы мысли учащихся на пути поиска решения задачи? и т.д. Ответы на них учитель получает, задав вопросы: «Почему?», «На каком основании?» и др.
Следовательно, педагог должен обладать искусством постановки проблемных вопросов. На первых порах следует начинать с общего вопроса, далее конкретизировать вопросы, пока не будет найден тот, который соответствует уровню развития учеников. Вопросы должны повторяться часто и в разнообразных ситуациях, тогда они будут усвоены учащимися и обратятся в привычную функцию ума. Все вопросы, которые учитель предполагает задавать учащимся на уроках, должны быть заранее и тщательно продуманы, видоизменение их возможно в процессе занятия.
Например, при решении задач можно задавать вопросы, в которых присутствует полное или частичное сравнение: «В чём сходство и различие ромба и квадрата?», «В чём сходство и различие между тетраэдром и параллелепипедом?», «В чём сходство между четырёхугольной призмой и кубом?», «Чем отличается двойка от произвольного составного числа?»
Лишь при осуществлении таких умственных операций (сопоставление видовых и родовых понятий) установление связей между ними позволит дать правильные ответы на поставленные вопросы.
Способствуют мыслительной деятельности и вопросы, в которых нужно установить основные характерные черты, признаки понятий и предметов. Вопросы могут быть такого характера: «Является ли параллельность противоположных сторон характерным признаком прямоугольника?», «Может ли равенство всех сторон многоугольника быть характерным признаком правильного многоугольника?», «Две прямые лежат в одной плоскости. Может ли это свойство быть признаком параллельности прямых?»
Полезными будут вопросы, которые устанавливают причинно-следственные связи, при ответе на них осуществляется движение «от частного к общему», «от общего к конкретному», требуется установить справедливость обратного утверждения.
Учитель в школе, задавая учащимся вопрос, должен дать им возможность сначала подумать и потом требовать правильный ответ, так как для формирования мышления очень важно, чтобы ученик объяснил, как он шел к решению данной задачи, какие делал попытки, почему от них отказался и т.д. При такой постановке обучения учитель получит представление о ходе размышлений учащегося и может судить о степени развитости его мышления.
Таким образом, мы постарались показать, что в основе методов обучения должен лежать психологический анализ процесса усвоения, т.е. анализ того, как учащийся мыслит. Важно осознать, что понимание сути математики – это не отдельный акт, а процесс, очень сложный и длительный. Учащийся постепенно проникает в суть предмета, его представления постепенно принимают правильную форму.
Выше мы лишь на ряде примеров указали учителю математики на значение психологии для решения проблем обучения математике. В дальнейшем кратко остановимся на исследованиях видных психологов о мышлении, результаты исследований которых можно применить в обучении математике.
Психолог с мировой известностью Л.С. Выготский подчеркивал, что мышление является «одним из труднейших, запутаннейших и сложнейших вопросов экспериментальной психологии» [1]. С.Л. Рубинштейн [5] отмечал, что мышление – есть «движение мысли», но ведь, ни что такое «мысль», ни что такое «ее движение», нам совершенно не известно. Таким образом, дефиниции С.Л. Рубинштейна, Л.С. Выготского, данные понятию «мышление», мало что дают.
Основным средством становления культуры мышления в контексте математического образования является учебная деятельность, адекватная творческой математической деятельности. Необходимым условием развития выступает активность самого обучаемого в учебно-познавательной деятельности, причем активность внутренняя, делающая его субъектом деятельности. Для этого необходимо, прежде всего, обеспечить интерес к надлежащему усвоению математического материала. Материал должен быть посилен для ученика, а его усвоение правильно организовано через собственную работу самих обучаемых с новыми знаниями. Как справедливо подтверждает Л.С. Выготский [1], знания усваиваются только в ходе работы учащегося с этими знаниями. Обучение, как показал Л.С. Выготский, создавая зону ближайшего развития, вызывает к жизни, приводит в движение внутренние процессы развития: то, что ребенок на данном этапе обучения делал под руководством и с помощью взрослого, он, научившись, будет делать сам. Поставленная перед ребенком задача перейдет из зоны ближайшего развития в зону актуального развития. Таким образом, обучение должно вести за собой развитие, «забегать вперед» развития. «Педагогика должна ориентироваться не на вчерашний, а на завтрашний день детского развития. Только тогда она сумеет в процессе обучения вызвать те процессы развития, которые сейчас лежат в зоне ближайшего развития» [1, с. 381].
По системе П.Я. Гальперина [2] важно, чтобы вначале ученик обязательно понял, какой материал надо усвоить и как с ним работать; затем организовать собственную работу ученика с материалом таким образом, чтобы можно было судить о ней не только по конечному результату, но и иметь возможность контролировать каждый ее шаг. Таким образом, первым шагом, первым этапом усвоения всегда было обеспечение понимания того, что дети должны усвоить. Теория П.Я. Гальперина предоставляет в распоряжение учителя достаточно четкие и достаточно конкретные рекомендации, позволяющие правильно организовать понимание. Вычленив некоторую порцию материала, математическое содержание которой дети должны усвоить, учитель обдумывает, какая именно работа учеников соответствует этому материалу, так как основная цель этого первоначального знакомства – подготовить школьников к самостоятельному выполнению нужной работы.
С точки зрения теории П.Я. Гальперина просто надо предоставить в распоряжение детей такие краткие схематические записи – конспекты материала и способов работы с ними, которые позволяют, ничего предварительно не заучивая, непосредственно после разъяснений учителя приступить к самостоятельной работе с новыми знаниями.
В системе организации обучения, предложенной П.Я. Гальпериным, контроль над работой ученика должен присутствовать только с целью помочь ученику избежать возможных ошибок. Но такой контроль должен быть очень коротким, с постепенным переходом к самоконтролю.
Рассмотрим трактовку С.Л. Рубинштейна и его высказывание о «механизмах» мышления. Трактовка дает очень многое, она является для нас отправной точкой в процессе изучения взаимосвязей мышления и обучения математике. Л.С. Рубинштейн пишет: «Процесс мышления – это прежде всего анализирование и синтезирование того, что выделяется анализом; это затем абстракция и обобщение, являющиеся производными от них. Закономерности этих процессов в их взаимоотношениях друг с другом – суть основные внутренние закономерности мышления» [6, с. 136]. В психологии мышление изучается в процессе решения задач. В ходе поиска решения человек осуществляет анализ, синтез, сравнение и прочие логические приемы мышления.
Анализ – это мысленное разделение целого предмета на важные элементы в определенном порядке, изучение каждого элемента в отдельности как части единого целого. Анализ в первую очередь используется для поиска пути решения. Для этого необходимо:
1) расчленить изучаемый объект на составные элементы;
2) исследовать каждый элемент;
3) если нужно, включить изучаемый объект в связи и отношения с другими;
4) составить план изучения объекта в целом.
Синтез – соединение частей или свойств изучаемого объекта в единое целое. Для осуществления синтеза надо объединить свойства, полученные при анализе.
Таким образом, чтобы найти способ решения, пользуются анализом, а найденное решение задачи обычно излагают синтетическим методом. После завершения анализа нередко требуется заново провести синтетическое рассуждение, чтобы оформить и изложить найденное решение. Анализ в большей мере способствует развитию мышления и творческих способностей. Анализ требует большей затраты учебного времени, но зато позволяет показать ученику, как найти решение, как можно самому догадаться ее решить. Если систематически использовать анализ, у учащегося сформируются навыки поиска решения задач [3]. Анализ в чистом виде вообще не применяется. Если ученик пользовался им при поиске решения задачи, то только до тех пор, пока в его сознании не возникнет идея решения. При решении задач синтезом в сознании человека проводится и анализ, но часто настолько быстро, подсознательно, что ему кажется, будто он сразу увидел решение, не прибегая к анализу. Поэтому необходимо помнить, что нет «чистого анализа», нет «чистого синтеза»: эти приемы взаимосвязаны.
Рассмотрим пример решения геометрической задачи: На плоскости прямоугольника ABCD в точку А восстановлен перпендикуляр на котором взята точка K. Отрезки KВ = 6 см, KС = 7 см, KD = 5 см. Найти АK.
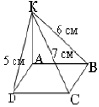
Представление данных на чертеже
1. Условием является все, что стоит до вопроса задачи.
2. Делаем чертеж (рисунок) и отмечаем на нем данные и искомые величины.
3. Чтобы ответить на вопрос задачи, надо найти стороны ΔDKC.
4. АK можно найти по теореме Пифагора из ΔАKB.
5. ABCD по условию прямоугольник, поэтому АВ = DС.
6. ΔDKC – прямоугольный, по теореме о трех перпендикулярах.
7. По теореме Пифагора находим DС, стороны прямоугольного треугольника – стороны KD и KС известны. Это есть анализ.
Движение по данной схеме к началу будет синтезом.
При решении математических задач анализ может выступать в двух формах:
а) когда в рассуждениях двигаются от искомых к данным задачи;
б) когда целое расчленяют на части.
Точно так же и синтез может выступать в двух формах:
а) когда движение осуществляется от данных к известным фактам;
б) когда элементы объединяют в одно целое.
Приведем пример рассуждения, когда используется синтез в форме (а).
Доказать тождество
sin20°•cos20°•cos40°•cos80° = 1/8.
С этой целью умножаем и делим выражение в левой части на sin20°.
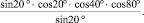
Далее ученики догадываются, что к числителю нужно применить формулу синуса двойного аргумента, и последовательно переписывает выражение в виде
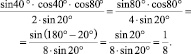
При исследовании процесса взаимосвязи мышления и обучения математике установлено, что «анализирование» и «синтезирование» – это не в чистом виде приемы мыслительной деятельности. Главными основными приемами мыслительной деятельности являются «анализ» и «синтез», а «анализирование» и «синтезирование» – это уже виды аналитико-синтетической деятельности, которые лежат в основе познания всех процессов вообще. Поэтому осознав, что все приемы мышления (абстрагирование и обобщение) являются производными анализа и синтеза, мы хотим сделать процессы «анализирования» и «синтезирования» рабочими методами процесса поиска решения задач.
В заключение хотелось бы отметить, что мы не ставили здесь себе цели систематического изложения определенных вопросов психологии и педагогики в процессе обучения математике. Мы лишь хотели путем отдельных замечаний и примеров обратить внимание на те проблемы этих наук, которые необходимы при обучении математике в школе.