Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Поиск методов становления знаний творческой базой компетентностности специалиста для решения конкретных профессиональных задач подводит высшую школу к поиску методов формирования творческой самостоятельности студентов в предметном обучении и качественном становлении личности в единой целостности.

Творческая деятельность – всякая практическая или теоретическая деятельность человека, в которой возникают новые (по крайней мере, для субъекта деятельности) результаты.

В педагогической энциклопедии творчество определяют как «высшую форму активности и самостоятельности человека» [1].

Я.А. Пономарев [2] определил творческий процесс четырьмя фазами классификации: первая фаза – сознательная работа, называемая «подготовкой»; вторая фаза заключается в бессознательной работе над проблемой, называемая «созреванием»; третья фаза, называемая «вдохновением», – поступление идеи решения в результате бессознательной работы в сферу сознания; четвертая – сознательная работа над оформлением и проверкой. Согласно Я.А. Пономареву, творческая деятельность, изменяя окружающий мир, меняет внутренний мир самого человека. Творчески мыслящий студент видит побочные результаты, которые являются творением нового, а нетворческий видит только результаты по достижению цели (целесообразные результаты), проходит мимо новизны.

С.Л. Рубинштейн самостоятельность определяет как осознанное мотивирование действий и их обоснованность, неподверженность чужим влияниям, стремление и способность поступать в соответствии со своим личным убеждением [3].

А.И. Щербаков самостоятельность определил как «интегральное свойство личности, базирующееся на единстве ума, чувств, воли, характера…» [4].

Изучение проблемы творчества и самостоятельности многими исследователями указывает на их тесную связь, которая позволяет интегрировать эти понятия в категорию творческой самостоятельности. Для творчества надо обладать знаниями, умениями и навыками, а это, по определению П.И. Пидкасистого, один из факторов самостоятельности, значит, она является условием творчества. По мнению педагога П.И. Пидкасистого, «высшая школа постепенно, но неуклонно переходит от передачи студентам информации в готовом виде к управлению их самостоятельной учебно-познавательной деятельностью, к формированию у них опыта самостоятельной творческой работы [5].

Суть творческой самостоятельности воспринимается как единство созидающего, интеллектуального, волевого, активного факторов познавательной деятельности, выражающееся в приобретении навыков переноса приобретенных знаний, умений и навыков к решению новых проблем, комбинировании ранее известных способов деятельности для решения новых проблем.

Мы считаем, что творческая самостоятельность будущих инженеров есть интегративное качество личности, проявляющееся в стремлении и умении собственными силами обеспечивать личную ответственность за решение проблемных, ситуативных, профессионально-ориентированных задач будущего инженера.

К критериям сформированности творческой самостоятельности студентов мы относим: потребность в творческой деятельности (отношение к дополнительным заданиям, ее независимость в новых условиях, характер читательских запросов, стремление к участию в научной работе, познавательная «дотошность» и т.п.); самостоятельная постановка творческих задач; прогнозирование и самостоятельное определение эффективных путей решения задач; умение работать с источником информации; формирование опыта критического оценивания собственных успехов и неудач; личная ответственность за результаты деятельности; развитие коммуникативных умений.

Анализ основных направлений работы вуза, связанных с развитием профессиональной творческой самостоятельности студентов, приводит к выводу о том, что в массовой практике высшей технической школы не сложилась четкая система работы по развитию творческой самостоятельности студентов. Значимым показателем творческой самостоятельности является единство созидающего, интеллектуального, волевого и активного факторов учебной деятельности. Не любая деятельность может обеспечить положительную результативность в достижении желаемой цели, необходимо включение студента в специально организованную деятельность. Констатирующий эксперимент, проведенный нами среди студентов первого года обучения, показал наличие высокой степени мотивации в усвоении знаний и умений на уровне готовности к их творческому применению, что обеспечивается внутрипредметной и межпредметной интеграцией знаний, их использованием при решении нестандартных задач, сопровождением процессуальными средствами творческой деятельности, к которым мы относим компьютерные математические системы (КМС), и рефлексией результатов, позволяющей установить их соответствие поставленному целевому компоненту, выявление причин их возможного несоответствия, постановку задач дальнейшей деятельности.

Для организации творческой самостоятельности нами были использованы: возможности многоуровневого обучения с помощью компьютеризированного учебника, обеспечивающие индивидуальный самостоятельный поиск решения, интерес не только к результату деятельности, но и к самому процессу приобретения знаний, как к творческому труду, направленному на профессиональное саморазвитие личности студента; разделение группы в команды для систематического вовлечения студентов в процесс научного познания, состоящего из постепенно усложняющихся творческих заданий, обеспечивающих развитие творческого мышления в условиях учебного общения, как продуктивного процесса.

На первом, организационном, этапе формирования творческой самостоятельности для усиления понимания смысла и содержания математических операций, действий, формул работа студентов организуется с помощью электронного учебного пособия. Электронное учебное пособие, подготовленное автором, содержит файлы, организованные как документы КМС Mathematica (с расширением .nb). При запуске вначале появляется титульный лист, где имеется гиперссылка, открывающая оглавление. Содержание пособия включает наиболее трудоемкие темы из курса математики для технических вузов, являющиеся в дальнейшем практическим инструментом в математических методах обработки результатов профессиональной исследовательской деятельности. Каждая из тем пособия организована как отдельный файл, который можно вызвать из оглавления; в свою очередь, из каждого такого файла с помощью гиперссылок можно перейти к поясняющим отдельные вопросы файлам; так проявляется многоуровневость структуры учебника (рис. 1).

При трехуровневом обучении более сильным студентам в электронном учебном пособии достаточно иметь доступ к минимальной информации. Следующей по силе группе студентов учебное пособие указывает (подсказывает) основной алгоритм решения заданий. Третья, более слабая группа студентов, требует постоянной педагогической поддержки в выполнении вычислений и построении графиков. Эти студенты получают образцы решения с анализом и особенностями творческого решения прикладных, физических задач. Многоуровневая форма подачи учебного материала позволяет сделать процесс обучения более наглядным, индивидуально-ориентированным (рис. 2).

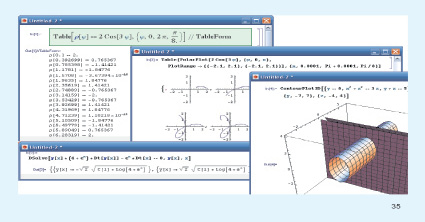
Рис. 1. Структура многоуровневого электронного учебника

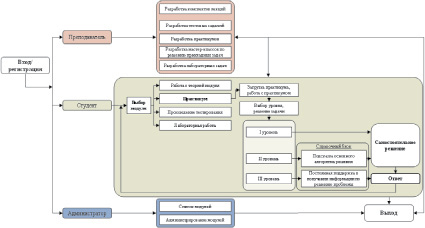
Рис. 2. Многоуровневая схема подачи учебного материала

Организация самостоятельной работы, включающей вариативность и компьютерную поддержку, ведет к повышению познавательного и творческого интереса, приводит к значительному расширению круга решаемых задач: если до применения КМС Mathematica в учебной группе решалось за установленное учебное время всего 5–6 задач, то теперь их количество исчисляется 10–12 задачами.

На втором, мотивационно-ценностном, этапе студенты, ориентируясь на потребностно-мотивационную сферу каждого, работая в команде, подбирают, изучают физические, прикладные задачи, знакомятся с историческими фактами различных открытий ученых в математике, инженерно-технической области, их обоснованием средствами математики, копируют исследовательскую деятельность ученого, следят за образом мыслей ученого, готовят презентации исследовательского проекта.

Преподаватель консультирует, дает рекомендации в решении проблемы, повышая степень творческой самостоятельности студентов. Этот этап включает репродуктивный, продуктивный типы воспроизведения и применения полученных знаний в виде решения по аналогии, превращение знаний в умения, активный поиск, открытие студентами новых знаний; поощряются обмен идеями, промежуточные просмотры, дружеские консультации.

На втором этапе, организованном как работа в команде, предполагается индивидуальное и коллективное творчество. В индивидуальном творчестве личность студента стремится к самовыражению. Коллективное творчество предполагает необходимость сотрудничества, взаимовыручки.

А.В. Ястребов считает, что «…обмен информацией между малыми группами или отдельными студентами является не просто удачным методическим приемом, не только хорошо обоснован с точки зрения психологии, но затрагивает существо математики – ее личностно-социальный дуализм, и в силу этого является в определенном смысле обязательным для процесса преподавания» [7].

Нельзя сказать, что все задачи вызывают живой интерес у студентов. Однако исследование студентами решения хотя бы одной задачи, работа в команде вносят положительные качественные изменения в психологическое настроение, содержание и структуру учебной деятельности студентов.

На третьем, подготовительном, этапе формирования проблемы профессионально-ориентированной задачи студенты выдвигают гипотезы, строится план решения задачи, варианты применения КМС Mathematica, готовится математическая модель решения подготавливаемой задачи. При составлении задач студенты придерживались следующих требований: во-первых, задачи должны быть занимательными по форме, содержанию, сюжету, по способу решения или неожиданному результату; во-вторых, задачи должны иметь практическую значимость; в-третьих, задания должны быть сформулированы так, чтобы их выполнение было невозможным без хорошего знания теоретического материала. Согласование тем курса математики и комплекса прикладных и профессионально-ориентированных задач представлено в таблице.

На четвертом, содержательно-исследовательском, этапе происходит повторное осмысление всех входящих в математическую модель величин, переменных, их влияние на рассматриваемые процессы, определяется их сущность, проводятся вычисления математическими методами и их проверка в КМС Mathematica.

На пятом, оценочном, этапе происходит сравнительный анализ полученных результатов с практическими данными, выявляются новые проблемы, возможности их решения, как следствие из решенной проблемы. В.В. Афанасьев считает, что при формировании творческой активности необходим самоанализ собственных интеллектуальных действий студентов. С помощью такого анализа осуществляется самоконтроль и самооценка проделанной работы, фиксируются рациональные структуры творческого процесса [8].