Результаты теоретического и экспериментального исследования процессов смачивания и растекания жидких фаз по поверхности твердых тел находят практическое применение во многих современных технологиях [2–8]. В связи с этим, несмотря на значительные успехи, достигнутые к настоящему времени при изучении этих процессов, задача их дальнейшего исследования остается актуальной.
Анализ результатов, полученных отечественными и зарубежными авторами в данной области, свидетельствует, что основная проблема при теоретическом исследовании процессов растекания связана с перемещением контактной линии, которое в уравнениях Навье – Стокса приводит к недопустимой сингулярности силы на этой линии при граничных условиях прилипания.
Для устранения сингулярности силы при этом используют, как правило, два различных подхода. Первый связан с использованием в теоретической модели растекания условия скольжения в области контактной линии (условие Максвелла) вместо условия прилипания, при котором величина скольжения пропорциональна локальному градиенту скорости [8]. При втором варианте в гидродинамической модели растекания жидкости по поверхности твердого тела авторы учитывают расклинивающее давление [4].
Заметим далее, что если для макроскопических масштабов такое приближение (условие прилипания) на границе раздела жидкости с твердым телом во многих случаях вполне удовлетворительно, то для микроскопических масштабов из-за возможного скольжения жидкости относительно твердой поверхности такое приближение должно быть пересмотрено.
Рассмотрим каплю ньютоновской вязкой нелетучей жидкости, которая находится на гладкой горизонтальной твердой поверхности. Ограничимся здесь рассмотрением двумерной капли, когда модель описывает случай растекания бесконечного валика жидкости в направлении, перпендикулярном его оси. В произвольном сечении такой двумерной капли введем декартову систему координат Oxz с осью Ox, направленной горизонтально по непроницаемой поверхности твердого тела, вертикальной осью Oz и точкой O, расположенной в центре пятна смачивания. Полагаем в дальнейшем сечение капли симметричным относительно оси Oz и ограничимся рассмотрением лишь одной ее половины, соответствующей x > 0.
Для описания движения двумерной капли в рассматриваемой системе воспользуемся уравнениями Навье – Стокса в приближении «теории смазки» [3]. С учетом действия гравитационных сил эти уравнения запишутся в виде
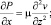
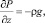(1)
где v – горизонтальная компонента скорости; P – давление в жидкой фазе; μ – вязкость жидкости; ρ – ее плотность; g – ускорение силы тяжести.
Для рассматриваемой задачи гравитационного растекания отсутствие касательных напряжений на границе раздела жидкость – газ имеет вид
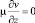при z = f(x, t), (2)
где z = f(x, t) – профиль свободной поверхности двумерной капли в момент времени t.
Принимая во внимание указанное выше обстоятельство и специфику исследуемой задачи, примем на границе раздела жидкость – твердое тело условие
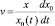при z = 0, (3)
где x0 – абсцисса точки трехфазного контакта (радиус растекания капли).
Заметим, что (3) сочетает в себе условие прилипания в центре капли (x = 0) с перемещением точки трехфазного контакта (x = x0(t)) со скоростью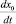 
.
Для рассматриваемого двумерного случая условие сохранения площади сечения (объема) валика в любой момент времени t, с учетом ее симметрии, запишется в виде нелокального интегрального условия
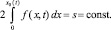(4)
Интегрируя первое уравнение (1) и пользуясь граничным условием (2), получим
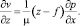(5)
Интегрирование (5) с условием скольжения (3) дает выражение для горизонтальной составляющей скорости:
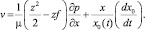(6)
Воспользуемся далее уравнением неразрывности, которое для рассматриваемого двумерного случая имеет вид
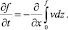(7)
Подстановка в уравнение неразрывности (7) выражения для скорости (6) дает
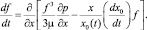(8)
Давление в жидкой капле без учета действия капиллярных эффектов определяется тогда выражением
p = p0 – ρg(z – f), (9)
где p0 – давление в газовой среде над каплей.
Подстановка (9) в (8) дает окончательно уравнение растекания двумерной капли в гравитационном поле с учетом эффекта проскальзывания:
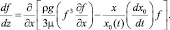(10)
Для исследования уравнения (10) проведем далее, как в [3], нормализацию переменных с характерными значениями времени t*, высоты поверхности капли f* и горизонтального размера x*. В нормализованных переменных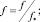 
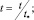
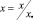получим из (10) уравнение растекания в безразмерной форме
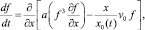(11)
где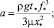 
v0 – безразмерная скорость растекания.
Условие сохранения площади сечения двумерной капли (4) в любой момент времени в безразмерных переменных примет вид
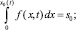
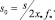(12)
Отметим, что даже в рассматриваемой двумерной постановке уравнение (11) с соответствующими дополнительными условиями неразрешимо прямыми аналитическими методами, а ее численное решение связано с большими трудностями из-за высокого порядка уравнения, его нелинейности и неклассического интегрального условия (12).
Для получения приближенного решения исследуемой задачи применим квазистационарный подход [1, 3], позволяющий свести задачу растекания от нелинейного дифференциального уравнения в частных производных к обыкновенному дифференциальному уравнению с соответствующими дополнительными условиями. Суть данного подхода состоит в том, что скорость распространения точки трехфазного контакта вначале полагается постоянной, а затем находится на основе кинематической зависимости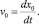 
Выполним в (11) переход к новым переменным
ξ = x – x0(t);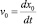 
(13)
и, временно «замораживая» скорость растекания капли v0, получим
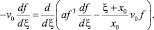(14)
После интегрирования (14) имеем соотношение
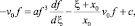c = const. (15)
Граничное условие
f = 0 при ξ = 0, (16)
которое выражает равенство нулю высоты капли в точке трехфазного контакта, приводит к нулевому значению постоянной интегрирования: с = 0.
Тогда из (15) получим уравнение
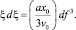(17)
Отсюда, после интегрирования (17) с учетом условия (16), имеем
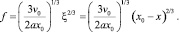(18)
Чтобы установить зависимость между радиусом и скоростью расстояния капли, воспользуемся (18) и нелокальным интегральным условием (12). Тогда получим
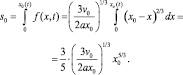(19)
Далее из (19) c учетом зависимости скорости от радиуса растекания получаем уравнение растекания
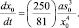(20)
Интегрирование (20) с использованием начального условия
x0(t) = x0(0) при t = 0 (21)
дает зависимость
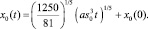(22)
В квазистационарном приближении форма поверхности капли с условием скольжения по твердой поверхности, в силу (18) и (20), определяется тогда зависимостью
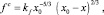kf ≈1,667, (23)
где принято s = 2x*f*.
Для оценки влияния эффекта проскальзывания на решение задачи растекания двумерной капли на твердой поверхности приведем ниже известное автомодельное
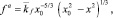
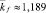(24)
и квазистационарное
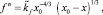
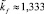(25)
решения данной задачи с условиями прилипания [3].
Из (23)–(25) следует, что наибольшей толщины f0 (высота в апексе) капля достигает во всех случаях в центре (x = 0) и они соответственно равны
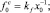
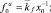
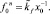(26)
Заметим далее, что при одинаковой высоте капли в любой момент времени в апексе, абсциссы точек трехфазного контакта квазистационарных решений задачи с условиями скольжения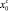 
и прилипания 
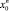, а также автомодельного решения с условием прилипания 
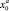, связаны зависимостью
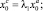
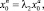
λ1 ≈ 1,402, λ2 ≈ 1,121. (27)
Скорость растекания капли в трех рассматриваемых случаях можно представить в виде
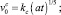
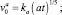
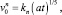(28)
где kc = 0,346, ka = 0,282, kn = 0,263.
Для оценки поведения кривых, описывающих профили свободной поверхности капли в апексах и точках трехфазного контакта, продифференцируем (23)–(25) и соответственно получим
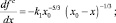
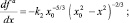
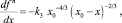(29)
где k1≈ 1,111, k2 ≈ 0,752, k3 ≈ 0,444.
Переходя к пределу при x > x0 и x > 0 в формулах (29), заключаем, что в точках трехфазного контакта касательная к свободной поверхности капли во всех трех случаях перпендикулярна оси Ox, в апексе касательная к поверхности капли, в случае автомодельного решения, направлена перпендикулярно оси Oz, а при квазистационарных решениях с условиями скольжения и прилипания направлена к оси абсцисс соответственно под углами
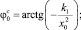
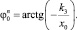(30)
Таким образом, проведенный сравнительный анализ известных автомодельного и квазистационарного решений задачи гравитационного растекания с полученным квазистационарным решением данной задачи с условием скольжения показывает, что несмотря на некоторое отличие форм поверхности капли в указанных решениях основные характеристики процесса оказываются схожими. Например, в обоих подходах точка трехфазного контакта со временем перемещается по поверхности твердого тела по степенному закону и эти зависимости количественно незначительно отличаются числовыми множителями.
Полученный в работе результат показывает, что квазистационарное решение задачи гравитационного растекания с учетом эффекта проскальзывания, с определенными оговорками, дает приемлемую точность решения и позволяет качественно адекватно описывать моделируемый физический процесс.
Полученный результат представляет не только самостоятельный интерес, но и может служить определенным тестом при построении и исследовании математических моделей более высокого иерархического уровня, например при численном исследовании модели данной задачи на основе нелинейного уравнения в частных производных с нелокальным интегральным условием.