Современный подход к решению технологических задач с использованием методов математического моделирования основан на принципах системного анализа [3]. Согласно этим принципам технологический процесс и его математическая модель рассматривается как сложная система, состоящая из элементов различных уровней детализации: от атомного до отдельного процесса и далее, до совокупности технологических процессов. Сущность системы невозможно понять, рассматривая только свойства элементов; для неё существенны как способ взаимодействия элементов, так и взаимодействие элементов или системы с окружающей средой [9].
При моделировании технологии изготовления композитов специального назначения будем выделять несколько уровней иерархии, между которыми существуют отношения соподчиненности. На первом уровне располагаются модели элементарных процессов технологии (химические, массообменные, тепловые, механические, гидромеханические), на более высоких – модели, направленные на решение оптимизационных задач, синтеза систем, которые выделяются по какому-либо признаку. При анализе отдельного процесса в качестве элементов или ступеней иерархии могут выступать явления, в совокупности определяющие целевую функцию процесса, например химическое превращение, теплообмен и т.д. Основная идея системного анализа композиционных материалов (КМ) состоит в применении общих принципов разделения (декомпозиции) системы композита на отдельные элементы и установление связей между ними, в определении цели исследования и установления этапов для достижения этой цели [1, 8].
Системный подход к моделированию технологии композитов имеет цель получения оценок функционирования процесса на каждом уровне декомпозиции (макроуровень, мезоуровень, микроуровень) и осуществляется в несколько этапов. Отдельный элемент системы моделирования в зависимости от поставленной цели рассматривается как отдельная система с более детализованными уровнями декомпозиции.
Отличительной особенностью моделирования композиционных материалов от моделирования механической смеси компонентов (свойства которой определяются как сумма свойств компонентов) является наличие границы раздела фаз, определяющей интенсивность процессов структурообразования и свойства материала (системы). На границе раздела фаз формируется контактный слой, обеспечивающий сцепление компонентов (адгезионную прочность – новое интегративное свойство, которым не обладают входящие в систему элементы) и свойства материала [2]. Объединение компонентов в ходе многокритериального синтеза композитов приводит к образованию на границе раздела фаз слоев с измененными свойствами (сольватный слой), оказывающими влияние на процессы формирования свойств системы, принципиально отличающихся от характеристик исходных компонентов и обеспечивающих появление уникальных свойств композитов (например, радиационно-защитные свойства), что соответствует принципу эмерджентности [2].
Многокритериальный синтез обуславливает необходимость выбора критериев оптимальности, среди которых выделим частные критерии и интегральные (обобщенные). Оценку и сравнение КМ будем производить, используя интегральные (обобщенные) критерии, в которых учитывается ряд наиболее важных частных критериев.
Выбор обобщенного критерия эффективности производится в зависимости от поставленной задачи. А так как задачи, выполняемые композиционными материалами, различны, то в каждом конкретном случае используется свой критерий эффективности, который считается наиболее целесообразным и учитывающим особенности материала и область его применения, т.е. отсутствует универсальный обобщенный критерий для любой системы.
В практике определения эффективности КМ нашло применение достаточно большое количество обобщенных критериев, основные из которых приведены на рисунке. На основе приведенной классификации рассмотрим основные методы формирования таких критериев и дадим им сравнительную оценку [10, 6, 5, 7].
1. Наиболее простой метод построения интегрального критерия заключается в том, что один из частных критериев уk принимается в качестве обобщенного, а все остальные учитываются в виде ограничений, определяющих область допустимых альтернатив:
E = yk;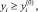 
i = 1, 2…, l;
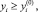i = l + l, l + 2, n i ≠ k, (1)
где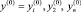 
– вектор, определяющий допустимые значения по всем критериям.
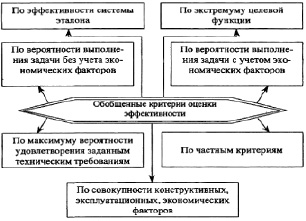
Классификация критериев оценки эффективности сложных технических систем
Варианты, не укладывающиеся в заданные границы, сразу же отбрасываются как неконкурентоспособные. Естественно, что практические рекомендации будут зависеть от того, как будут выбраны ограничения на вспомогательные частные критерии. При этом задача оптимизации формулируется как задача математического программирования:
Max [уk(a)], α ∈ A, y i(α) ≥ yi(0),
y i(α) ≤ yi(0), i = l + 1, l + 2 i ≠ k. (2)
Вид уk(а) и у(а) определяет метод программирования. Основным недостатком данного подхода в оценке эффективности композита специального назначения является то, что варианты сравниваются по одному критерию, значения других критериев, если они удовлетворяют ограничениям, не учитываются. Достоинство – сравнительная простота построения критерия.
2. Оценка эффективности КМ по эффективности системы-эталона. Под системой-эталоном понимается оптимальная, идеально функционирующая система (идеальный композит), которой соответствует вектор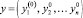 
, где компонентами являются максимальные значения для максимизируемых и минимальные значения для минимизируемых критериев. В этом случае обобщенные критерии могут быть сформулированы в виде:
1) суммы абсолютных отклонений от идеальной альтернативы для частных критериев одной размерности:
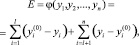(3)
где yi (i = 1, 2, ..., l) – частные критерии оптимальности, подлежащие максимизации; yi (i = l + 1, l + 2,..., n) – частные критерии, подлежащие минимизации;
2) суммы относительных отклонений для частных критериев различной размерности:
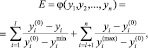(4)
где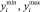 
– наименьшие значения для максимизируемых и наибольшие для минимизируемых критериев оптимальности по всему множеству вариантов;
3) наибольшего абсолютного отклонения от идеального для частных критериев одной размерности:
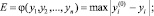(5)
4) наибольшего относительного отклонения от идеального для частных критериев различной размерности:
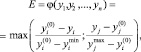(6)
где i = 1, 2,..., l; j = l + 1, l + 2...., n.
Применение таких критериев при оценке эффективности КМ ограничено случаями небольшого количества непротиворечивых частных критериев (шкала твердости), и применение подобных критериев для оценки, например, эффективности радиационно-защитных свойств композитов приводит к противоречию между множеством частных критериев (не учитывается ценность, полезность частных критериев yi) и затрудняет выбор системы-эталона.
3. Если известна математическая модель композита, устанавливающая последовательность зависимостей в виде формул, таблиц или систем алгебраических и дифференциальных уравнений, то задача оптимального проектирования состоит в том, чтобы для имеющейся совокупности добиться экстремума целевой функции (например, максимума плотности, прочности, минимума стоимости и др.) при наложении ограничений на параметры в виде
Bi min ≤ Bi ≤ Bi max. (7)
Однако далеко не всегда удается найти единственную непротиворечивую функцию цели, которая связывает всю совокупность параметров. Такая функция синтезируется в предложенной системе компьютерно-имитационного моделирования с последующим решением задачи отыскания экстремума.
4. Для некоторых композитов специального назначения эффективность может быть оценена по вероятности выполнения решаемых ими задач. Такая оценка, как правило, используется при оценке эффективности военно-технических систем. Следует отметить, что этот критерий полностью характеризует главное назначение системы. Этот критерий во многих случаях может быть представлен в виде вероятностной модели и вычислен. Однако он односторонне оценивает систему, не связан явно с технологическими и экономическими показателями, такими как прочность, плотность, коэффициент линейного ослабления, стоимость, эксплуатационные характеристики и др. Он может быть использован при наличии определенного объема статистических данных, которые при разработке нового композита, как правило, отсутствуют.
5. Использование в качестве обобщенного критерия вероятности выполнения решаемых КМ задач, но с учетом экономических факторов. Например, эффективность КМ может определяться в самом общем виде как соотношение нанесенного (или предотвращенного) ущерба D к затратам на нанесение (предотвращение) ущерба С/Е = D/C. Этот критерий эффективности полностью характеризует главное назначение КМ и учитывает, какой ценой достигается эффект. Однако использование подобных критериев при моделировании затруднено, так как отсутствуют функциональные связи D и С с технологическими и эксплуатационными параметрами КМ.
Краткая сравнительная оценка рассмотренных обобщенных критериев показывает, что моделирование и определение эффективности КМ является сложной задачей, особенно при учете ряда частных показателей, таких как качество процесса управления, надежность, плотность и т.д. Как правило, эти показатели трудно аналитически связать с обобщенным критерием, что затрудняет использование таких критериев.
Для оценки эффективности и качества КМ при моделировании предлагается способ формирования критерия предпочтения, являющийся модификацией метода последовательных уступок. Согласно предложенному способу при формировании критерия предпочтения выполняется следующий алгоритм.
1. Из совокупности частных показателей выбирается один, который в дальнейшем рассматривается как основная функция цели у1.
2. По выбранному критерию у1 производится оптимизация системы при учете только технологических ограничений. При этом определяются не только экстремальные значения у1 и соответствующие значения параметров оптимизации, но и величины других рабочих показателей, которые рассматриваются в качестве неосновных функций цели.
3. Вводится некоторая уступка Dу1 по основному показателю, и система оптимизируется поочередно по всем неосновным функциям цели при условии, что ограничения на другие критерии, кроме основного, не принимаются во внимание. Определяются лучшее yjл и худшее yjx значения каждого неосновного критерия и соответствующие им значения параметров оптимизации. Этот пункт может выполняться несколько раз при разных значениях Dу1, и при этом может оцениваться влияние Dу1 на результаты оптимизации по неосновным показателям.
4. Результаты, полученные на предыдущем шаге, используются для нормирования неосновных критериев. Вводится функциональная зависимость m(уj), определяющая изменение j-го критерия в интервале от худшего до лучшего. Эту функцию назовем функцией принадлежности. В первом приближении можно говорить о линейной зависимости, т.е.
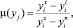(8)
где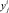 
– векторное промежуточное (текущее) значение j-го критерия.
5. После определения, таким образом всех функций принадлежности для всей совокупности неосновных критериев формируем общую функцию принадлежности:
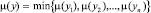. (9)
Введение общей функции принадлежности обеспечивает получение результата по любому критерию не ниже заданного уровня, если этот уровень достижим в конкретных условиях.
6. Производится сопоставление основного критерия оптимальности функции принадлежности, объединяющей неосновные критерии, и вводится функция принадлежности по всем критериям. При этом лучшее значение основного критерия получается в результате частной оптимизации, а в качестве худшего значения принимается уровень, ухудшенный по отношению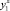 
на величину уступки.
Далее формируется функция принадлежности
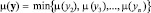(10)
и осуществляется поиск варианта проекта, удовлетворяющего условию (10).
Последнее выражение означает, что определяется вариант, дающий максимальный уровень функции (9). При этом найденный вариант проекта должен находиться в области допустимых значений параметров оптимизации.
С целью учета системы эксплуатационных, технологических и экономических показателей качества КМ при моделировании автором предлагается обобщенный критерий практической оптимальности, основанный на аддитивном преобразовании [1, 2, 3]:
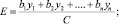
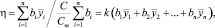(11)
где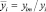 
– относительное значение показателя i-го качества; yi – абсолютное значение показателя; yim – максимально допустимое значение показателя; С – стоимость системы; Сm – максимально допустимое значение стоимости; bi – весовой коэффициент, который отражает полезность (ценность) i-го критерия при принятии решения о выборе альтернативы.
Приведение частных показателей к безразмерной относительной форме (второе уравнение) производится для того, чтобы весовые коэффициенты bi имели одинаковую размерность.
Предполагается проводить выбор частных показателей так, чтобы при их уменьшении Е увеличивалась (плотность, ошибка управления и др.). Поэтому в качестве показателя надежности следует принимать не вероятность безотказной работы, а вероятность отказа. Кроме того, некоторые параметры (а следовательно, частные показатели) изменяются дискретно. Также дискретно изменяется и обобщенный критерий. В практике моделирования возможен случай, когда Е отличается от оптимального. Такую систему назовем практически оптимальной (отсюда название рассматриваемого критерия), т.е. при наложенных ограничениях не может быть системы, имеющей большее значение Е.
Достоинством этого критерия эффективности является простота его вычисления. Он связан с назначением систем и обеспечивает учет при моделировании конструктивных, эксплуатационных и экономических факторов. Основная сложность при его применении заключается в определении весовых коэффициентов [1, 2].
Разработанный математический метод моделирования эффективности КМ использовался в комплексе программ компьютерно-имитационного моделирования КМ при формировании критерия оптимальности и функции качества для КМ на минеральной и полимерной основах для защиты от радиации и показал свою эффективность [2, 3].
Статья публикуется при поддержке гранта № 3018 Базовой части Госзадания вузам.