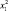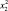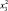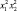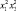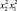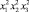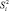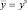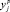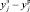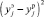Многолетний опыт разработки газовых и газоконденсатных месторождений нефтегазоносной области России требует научного обобщения и интерпретации с целью не повторения ошибок при освоении новых площадей. Главными проблемами при разработке залежей являются геологические, технологические и технические причины.
К геологическим причинам относят геологическое строение продуктивных отложений, осложненное разломами (трещинами) и тектоническими нарушениями, повышенное содержание солей, парафина, серы и т.д., физико-химический состав флюида и т.д.
К технологическим причинам относят затруднения по организации нефтегазосборной сети, системы заводнения залежи, работы промысловых бригад и специалистов, контроля за разработкой углеводородов и т.д.
К техническим причинам относят сложность организации инфраструктуры нефтегазодобывающего промысла (проведение дорог, водо- и электроснабжения, нефте/газопровода и т.д.), в условиях болотистой или плохо проходимой местности и сложнейших климатических условий.
Хотелось бы отметить, что именно технические проблемы первыми затормаживают организацию процесса добычи углеводородов как отложенного механизма.
Необходимость освоения новых месторождений газа, формирование соответствующей инфраструктуры при сложных географических, геологических и природно-климатических условиях добычи, а также увеличение дальности пригодных транспортных развязок будут негативно сказываться на экономических показателях работы предприятий по добыче и транспортировке нефти и газа.
Одним из способов сократить экономические затраты на разработку новых месторождений, отдаленных от уже имеющихся населенных пунктов севера Ямало-Ненецкого автономного округа, является использование существующих естественных условий окружающей природы в качестве основы для прокладки качественного и стойкого (достаточно долговечного) дорожного полотна. Такими дорогами являются насыпные, снеголедяные дорожные покрытия и зимники.
Механизация строительства зимних дорог может развиваться по двум направлениям. Первое из них основано на применении специализированных машин, выполняющих одновременно (по совмещенной технологии) перемешивание и увлажнение снега, его уплотнение и рифление покрытия дорожного полотна. Второе направление состоит в использовании универсальных машин и простого навесного или прицепного оборудования, выполняющего технологические операции последовательно (по расчленённой технологии).
Специализированные машины, работающие по совмещенной технологии, не позволяют строить зимние дороги в насыпи. Для собирания снега с дорожной полосы при сооружении насыпи требуются отдельные машины – снегоочистители. Недостатком специализированных машин является также их непригодность для эксплуатационного обслуживания зимних дорог. По этим причинам общепризнаны преимущества расчлененной технологии сооружения зимних дорог и ледовых переправ.
Расчлененная (пооперационная) технология сооружения зимней дороги включает в себя различный набор операций в зависимости от конструкции полотна дороги и принятого способа его строительства.
Для эффективного уплотнения снежной массы нужно произвести поиск и выявить факторы, влияющие на этот процесс. Из анализа литературных источников и по результатам экспериментов предыдущих исследований, проводимых А.В. Шарухой, А.Л. Егоровым, Ш.М. Мердановым и др. [1–9], выделены для дальнейшего исследования следующие факторы: количество проходов установки n, ед.; масса установки – m, кг; частота колебаний вибратора – v, Гц.
Остальные факторы зафиксированы: ширина уплотняемого снежного покрова – S = 570 мм; начальная толщина снежного слоя – h = 420 мм; начальная плотность снежной массы – r = 287 кг/м2; погодные условия: температура окружающей среды Т = 0 °С, атмосферное давление р = 737 мм рт.ст., влажность воздуха – 53 %, скорость ветра Vветр = 2 м/с, направление ветра – юго-западное.
После проведения выбора параметров, влияющих на уплотнение снежной массы был произведен расчет влияния факторов, которые были определены методом неполноблочных планов [14] в ходе которого было выявлены наиболее значимые: частота и амплитуда вибрационного уплотняющего воздействия, масса и количество проходов гидрошинного катка. Значения уровней и интервалов варьирования факторов приведены в табл. 1.
Таблица 1
Значения уровней и интервалов варьирования факторов
|
Наименование и обозначение факторов |
Уровни варьирования |
Интервалы варьирования |
||
|
–1 |
0 |
+1 |
||
|
Количество проходов установки n, ед. |
1 |
2 |
3 |
1 |
|
Масса установки – х2, кг |
420 |
500 |
580 |
80 |
|
Частота колебаний вибратора – х3 Гц |
20 |
35 |
50 |
15 |
Изменение частоты колебаний вибратора обеспечивалось путем использования частотного преобразователя – iG5. Скорость движения установки регулировалась путем запасовки канатов через блоки, для увеличения тягового усилия лебедки. Масса установки регулировалась за счет нагружения или снятия дополнительного груза (мешки с песком по 40 кг).
Для уменьшения влияния случайных ошибок работа выполнялась в одно время суток и одним исследователем. Подсчет несущей способности уплотненного дорожного основания производился путем взятия керна из уплотненной за один проход снежной массы [10–13] и взвешивания его на электронных весах и замера рулеткой высоты керна. Для вычисления использовалась программа Microsoft Excel, Regress, Statistics 10. Число повторных опытов – 3.
Число возможных опытов определяют по выражению
N = pk, (1)
где N – число опытов; р – число уровней; k – число факторов.
Был произведен эксперимент типа N = 23, где число факторов k = 3, число уровней р = 2, число опытов N = 8, число повторных опытов n = 3.
Обычно оптимизируется одна функция, наиболее важная с точки зрения исследования, при ограничениях, налагаемых другими функциями. Поэтому из многих выходных параметров выбирается один в качестве параметра оптимизации, а остальные служат ограничениями. Всегда полезно исследовать возможность уменьшения числа выходных параметров. Для этого можно воспользоваться корреляционным анализом.
Полином второй степени в общем виде имеет вид
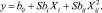(2)
Уравнение регрессии N = 23, по которому была сформирована матрица планирования эксперимента, представленная в табл. 2.
После проведения опытов была выполнена статистическая обработка результатов. Определим ошибки повторных (параллельных) опытов.
Среднеквадратичное отклонение определяем по выражению
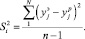(3)
Данные расчетов сведены в табл. 3.
Таблица 2
Матрица планирования эксперимента N = 23
|
№ п/п |
Матрица планирования |
Рабочая матрица |
Результаты параллельных экспериментов y1, y2, y3 |
|
||||||||||||||||
|
х0 |
x1 |
x2 |
x3 |
x1x2 |
x1x3 |
x2x3 |
x1x2x3 |
|
|
|
|
|
|
|
Количество проходов установки х1, ед. |
Масса установки – х2, кг |
Частота колебаний вибратора – х3 Гц |
|||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
1 |
1 |
–1 |
1 |
1 |
1 |
–1 |
–1 |
1 |
–1 |
1 |
1 |
1 |
–1 |
1 |
1 |
3 |
580 |
20 |
339,3 |
334,6 |
|
339,3 |
||||||||||||||||||||
|
325,2 |
||||||||||||||||||||
|
2 |
–1 |
–1 |
–1 |
–1 |
1 |
1 |
–1 |
1 |
–1 |
1 |
–1 |
1 |
–1 |
–1 |
1 |
1 |
580 |
20 |
396,3 |
395,8 |
|
395,8 |
||||||||||||||||||||
|
395,2 |
||||||||||||||||||||
|
3 |
1 |
1 |
–1 |
1 |
–1 |
1 |
1 |
1 |
–1 |
–1 |
–1 |
–1 |
–1 |
–1 |
1 |
3 |
420 |
20 |
354,5 |
356,4 |
|
354,5 |
||||||||||||||||||||
|
360,2 |
||||||||||||||||||||
|
4 |
–1 |
–1 |
–1 |
1 |
1 |
–1 |
1 |
–1 |
–1 |
–1 |
–1 |
–1 |
–1 |
1 |
1 |
1 |
420 |
20 |
316,0 |
318,1 |
|
322,3 |
||||||||||||||||||||
|
316,0 |
||||||||||||||||||||
|
5 |
1 |
1 |
1 |
1 |
–1 |
1 |
1 |
–1 |
–1 |
1 |
–1 |
1 |
–1 |
1 |
1 |
1 |
420 |
50 |
332,9 |
333,7 |
|
328,9 |
||||||||||||||||||||
|
339,3 |
||||||||||||||||||||
|
6 |
–1 |
–1 |
–1 |
1 |
1 |
1 |
1 |
–1 |
–1 |
1 |
1 |
1 |
1 |
1 |
–1 |
1 |
580 |
50 |
367,7 |
380,2 |
|
390,2 |
||||||||||||||||||||
|
382,7 |
||||||||||||||||||||
|
7 |
1 |
1 |
1 |
1 |
–1 |
–1 |
–1 |
–1 |
–1 |
–1 |
1 |
–1 |
1 |
1 |
–1 |
3 |
420 |
50 |
398,1 |
395,8 |
|
391,2 |
||||||||||||||||||||
|
398,1 |
||||||||||||||||||||
|
8 |
–1 |
1 |
1 |
1 |
1 |
1 |
–1 |
1 |
–1 |
–1 |
–1 |
–1 |
1 |
1 |
–1 |
3 |
580 |
50 |
426,3 |
428,7 |
|
428,3 |
||||||||||||||||||||
|
431,6 |
||||||||||||||||||||
Таблица 3
Данные расчетов
|
Номер опыта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
66,61 |
0,31 |
10,91 |
13,32 |
27,71 |
131,43 |
16,12 |
7,32 |
|
Si |
8,16 |
0,54 |
3,30 |
3,64 |
5,26 |
11,46 |
4,01 |
2,07 |
Таблица 4
Определение брака при повторных опытах
|
Номер опыта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
tрасч.мин |
–1,16 |
–0,91 |
–0,58 |
–0,58 |
–0,92 |
–1,09 |
–1,16 |
–0,9 |
|
tрасч.макс |
0,58 |
–1,03 |
1,16 |
1,16 |
1,07 |
0,87 |
0,58 |
1,07 |
|
tтабл |
4,3 |
4,3 |
4,3 |
4,3 |
4,3 |
4,3 |
4,3 |
4,3 |
Для определения брака используем критерий Стьюдента:
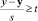или tрасч tтабл,
где t – критерий Стьюдента, его значение для 3 повторных опытов и доверительной вероятности 0,95 равно 4,3. Данные расчетов приведены в табл. 4.
Условие tрасч tтабл не выполняется. Дисперсия воспроизводимости рассчитывается по формуле
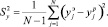(4)
Из расчета получаем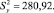 
Проверка однородности дисперсий выполняется по критерию Кохрена по формуле
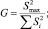(5)
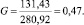
Для нахождения табличного значения Gтаб определяем N и f:
N = 8; f = 3 – 1 = 2; Gтаб = 0,515.
Условие Gp Gтаб выполняется, следовательно, дисперсии однородны.
Уравнение математической модели (полином 2 степени) с учетом парных взаимодействий имеет вид
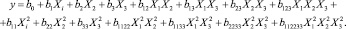
Вычисляем коэффициенты регрессии при полном факторном эксперименте по формуле
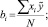(6)
b0 = –12,77; b1 = –1,37; b2 = –16,67; b3 = 288,41; b12 = 96,43; b13 = 96,22; b23 = 20,57; b123 = –10,72; b11 = –367,93; b22 = –14,13; b33 = –87,98; b1122 = –14,15; b1133 = –76,58; b2233 = 189,45; b112233 = 61,66.
С учетом значения дисперсии воспроизводимости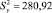 
с доверительной вероятностью a = 0,95 находим границы доверительных интервалов для коэффициентов регрессии:
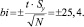(7)
Сравнивая значения коэффициентов регрессии с границами доверительных интервалов видим, что коэффициенты b0, b1, b2, b123, b11, b22, b33, b1122, b1133 незначимы. Теперь уравнение математической модели имеет вид
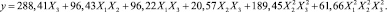
Таблица 5
Результаты расчетов
|
Параметр |
Номер серии опыта |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Сумма по всем сериям |
|
|
|
334,6 |
395,8 |
356,4 |
318,1 |
333,7 |
380,2 |
395,8 |
428,7 |
2943 |
|
|
338,4 |
386,8 |
352,1 |
310,2 |
340,1 |
379,1 |
401,5 |
419,4 |
– |
|
|
–3,8 |
9 |
4,3 |
7,9 |
–6,4 |
1,1 |
–5,7 |
9,3 |
15,8 |
|
|
14,2 |
80,1 |
18,6 |
62,4 |
40,6 |
1,3 |
32,2 |
86,7 |
336,1 |
Адекватность полученного уравнения проверяется путем вычисления теоретического значения параметра оптимизации yр, величины ошибки у = уэ – yр, результаты занесены в табл. 5.
Проверку адекватности математической модели выполняют при помощи коэффициента Фишера.
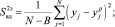(8)
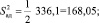
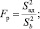(9)
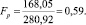
Определим число степеней свободы, d. f1 = 2 и d. f2 = 16. Выбираем уровень значимости = 0,95. По значениям d. f1 = 2 и d. f 2 = 16 находим критическое значение FT = 3,634.
Так как Fр FT, то математическое описание функции отклика уравнение регрессии считается адекватным.
Следующим этапом после планирования эксперимента является повторное проведение опытных исследований для уточнения и подтверждения гипотезы исследования.