При краткосрочном прогнозировании электропотребления возникает проблема, заключающаяся в учете действия определённых факторов на процесс электропотребления, к которым можно отнести статус дня (будний или праздничный/выходной) и фактор сезонности (в зависимости от включения/отключения системы отопления).
В силу различной степени действия перечисленных выше факторов на объект исследования значения параметров могут варьироваться достаточно широко, что влечёт за собой наличие выбросов в выборке, и, как следствие, увеличение величины ошибки прогноза. В связи с этим эффективным методом повышения качества получаемых прогнозных решений является кластеризация [8–9]. Данная процедура позволяет выделить кластеры, в которых значения необходимых показателей будут достаточно близки между собой. Последующие действия связаны с непосредственным прогнозированием на основе данных, находящихся в пределах обозначенных кластеров.
Далее в работе изложен анализ почасового прогнозирования электропотребления как без учёта кластерного подхода, так и с его применением.
Анализ прогнозных значений
В качестве методов прогнозирования широкое распространение получили статистические и интеллектуальные. Среди них были выбраны, согласно их преимуществам, приведённым в работах [5–6, 10], линейная регрессия, скользящие средние и нейросетевые методы. При прогнозировании почасового потребления электроэнергии Хакасии, МВт?ч, на временном лаге 3 месяца (6552 значения), получены значения средней абсолютной ошибки аппроксимации (MAPE), %, которые представлены в табл. 1. В качестве факторов, влияющих на динамику величины электропотребления, согласно [3–4, 7], использована информация о буднем (рабочем) или праздничном/выходном дне, сезонности в зависимости от подключения/ отключения системы отопления зданий. Инструментом прогнозирования являлась программа статистического анализа данных IBM SPSS Statistics v. 20 и стандартный офисный программный продукт MS Excel 2007.
Осуществлена проверка используемых данных об электропотреблении на нормальность закона распределения с применением критерия Колмогорова – Смирнова.
Полученные значения, представленные в табл. 2, указывают на несоответствие данных нормальному закону распределения, за исключением 5-го часа, где значение асимптотической значимости равно 0,078.
Таким образом, перечисленные выше методы прогнозирования не позволяют получить достаточно точные прогнозные решения, в результате чего необходимо использование механизма корректировки. Одним из эффективных методов повышения качества прогноза является предварительная кластеризация данных.
Кластеризация параметров заключается, согласно [1–2], в разбиении объектов на относительно схожие, однородные группы согласно некоторым признакам.
В качестве данных, подлежащих кластеризации, использованы и проанализированы ретроспективные статистические значения потребляемой электроэнергии на выбранном временном лаге (3 месяца). Поскольку динамика электропотребления по будним и праздничным/выходным дням отличается, то целесообразно разбить значения по выделенным ранее кластерам.
Таблица 1
Величины средних абсолютных ошибок прогнозных решений, полученных с помощью различных методов прогнозирования
|
№ п/п |
Метод прогнозирования |
Вид метода прогнозирования |
Средняя абсолютная ошибка (MAPE, %) |
|
1. |
Регрессия |
Линейная |
2,692 |
|
2. |
Скользящая средняя |
Простая (n = 14) |
2,07 |
|
Взвешенная (n = 16) |
2,344 |
||
|
Экспоненциальная (n = 6, K = 0,143) |
2,599 |
||
|
3. |
Нейронные сети |
Многослойный перцептрон |
2,072 |
|
Радиальная базисная функция |
2,799 |
Примечание. Параметр n – порядок скользящей средней; K – коэффициент сглаживания.
Таблица 2
Результаты одновыборочного критерия Колмогорова – Смирнова. Часы с ненормальным распределением данных
|
Параметры |
Час 0 |
Час 1 |
Час 2 |
Час 3 |
Час 4 |
Час 6 |
Час 7 |
Час 8 |
Час 9 |
Час 10 |
Час 11 |
Час 12 |
|
Статистика Z Колмогорова – Смирнова |
1,518 |
1,596 |
1,512 |
1,447 |
1,403 |
1,379 |
1,364 |
1,476 |
1,435 |
1,681 |
1,508 |
1,646 |
|
Асимптотическая значимость (двухсторонняя) |
0,02 |
0,012 |
0,021 |
0,03 |
0,039 |
0,045 |
0,048 |
0,026 |
0,033 |
0,007 |
0,021 |
0,009 |
Окончание табл. 2
|
Параметры |
Час 13 |
Час 14 |
Час 15 |
Час 16 |
Час 17 |
Час 18 |
Час 19 |
Час 20 |
Час 21 |
Час 22 |
Час 23 |
|
Статистика Z Колмогорова – Смирнова |
1,663 |
1,646 |
1,663 |
1,595 |
1,496 |
1,386 |
1,463 |
1,597 |
1,674 |
1,672 |
1,629 |
|
Асимптотическая значимость (двухсторонняя) |
0,008 |
0,009 |
0,008 |
0,012 |
0,023 |
0,043 |
0,028 |
0,012 |
0,007 |
0,007 |
0,01 |
Массив статистических данных электропотребления W(T, H, D) включает в себя факторы: T – время; H – сезон в зависимости от отопления; D – день (будний или праздничный/выходной). Кластеры, выделенные на основании фактора (признака) «Будний или праздничный/выходной день», могут быть записаны соответственно в виде Wfd(T, H) и Wdo(T, H), где Wfd(T, H) – кластер, содержащий данные об электропотреблении в будние дни; Wdo(T, H) – кластер, содержащий данные об электропотреблении в праздничные/выходные дни.
После проведения процедуры кластеризации выполнено прогнозирование параметра электропотребления, используя данные вышеобозначенных кластеров. Сопоставительные величины полученных средних абсолютных ошибок аппроксимации без использования кластеризации и при работе с кластерами Wfd(T, H) и Wdo(T, H) приведены в табл. 3.
Графические представления фактических и прогнозных значений на сутки вперёд с учётом и без использования кластеризации представлены на рис. 1–3.
Согласно табл. 3 и рис. 1–3, после проведения процедуры кластеризации по будним и праздничным/выходным дням средняя абсолютная ошибка прогноза уменьшена, при этом наибольшая эффективность наблюдается у метода простой скользящей средней.
Значения электропотребления по часам были проверены на соблюдение нормального закона распределения случайной величины. Электропотребление по будним дням, согласно критерию Колмогорова – Смирнова, с 0-го по 6-й часы, а также с 18-го по 19-й, подчиняется нормальному закону. Касательно асимптотической значимости в пределах другого выделенного кластера Wdo(T, H), она стала выше по сравнению с данными без использования кластеризации, указывая на соответствие величин нормальному закону распределения.
Детальные значения абсолютных прогнозных ошибок, отмеченные на проблемных часовых промежутках, а именно: с 8-го по 9-й, с 12-го по 13-й, с 17-го по 18-й часы, представлены в табл. 4. Данные участки охарактеризованы резкой сменой динамики изменения электропотребления, связанной с временем обеда, прихода и ухода с рабочих мест сотрудников в организациях и на предприятиях.
Таблица 3
Величины средних абсолютных ошибок прогнозных решений, кластеры «Будние дни» и «Праздничные/Выходные дни»
|
№ п/п |
Метод прогнозирования |
Вид метода прогнозирования |
Средняя абсолютная ошибка (MAPE, %) |
||
|
Все дни |
Будние дни |
Праздничные/ выходные дни |
|||
|
1. |
Регрессия |
Линейная |
2,69 |
1,6 |
2,44 |
|
2. |
Скользящая средняя |
Простая |
2,07 |
1,61 |
1,45 |
|
Взвешенная |
2,34 |
1,63 |
1,47 |
||
|
Экспоненциальная |
2,6 |
2,32 |
2,3 |
||
|
3. |
Нейронные сети |
Многослойный перцептрон |
2,07 |
1,93 |
1,73 |
|
Радиальная базисная функция |
2,8 |
2,63 |
1,91 |
||
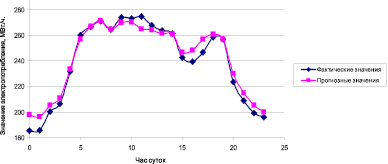
Рис. 1. Графики фактических и прогнозных значений электропотребления в Хакасии на сутки вперёд, метод простой скользящей средней, без кластеризации
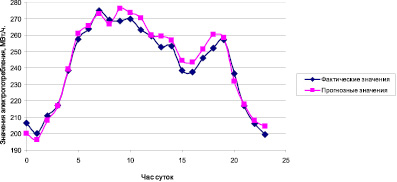
Рис. 2. Графики фактических и прогнозных значений электропотребления в Хакасии на сутки вперёд, метод простой скользящей средней, кластер «Будние дни»
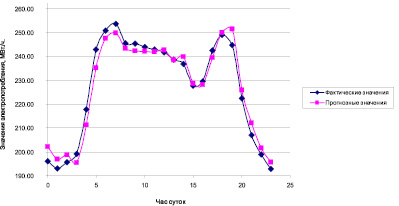
Рис. 3. Графики фактических и прогнозных значений электропотребления в Хакасии на сутки вперёд, метод простой скользящей средней, кластер «Праздничные/Выходные дни»
Таблица 4
Сравнение величин абсолютной ошибки прогноза, метод взвешенной скользящей средней, до и после проведения кластеризации
|
Час |
Значение абсолютной ошибки прогноза, %, без кластеризации |
Значение абсолютной ошибки прогноза, %, кластер «Будние дни» |
Значение абсолютной ошибки прогноза, %, кластер «Праздничные/выходные дни» |
|
8 |
0,09 |
0,96 |
0,94 |
|
9 |
1,55 |
2,89 |
1,25 |
|
12 |
1,36 |
0,25 |
0,34 |
|
13 |
0,89 |
2,65 |
0,1 |
|
17 |
4,1 |
2,17 |
1,26 |
|
18 |
0,95 |
3,23 |
0,44 |
Анализ табл. 4 позволил выявить частичное снижение величины прогнозной ошибки на указанных выше проблемных промежутках. Следует отметить, что до учёта кластерного подхода средняя абсолютная ошибка прогноза равнялась 1,5 %. При выполнении кластеризации значений электропотребления согласно признаку «Будний день» ошибка составила 2 %. При этом кластеризация с учётом признака «Праздничный/выходной день» позволила уменьшить значение прогнозной ошибки до 0,7 %. Однако проблема неудовлетворительного качества прогнозных решений по-прежнему остаётся на часах 9-й, 13-й и промежутке с 17-го по 18-й часы.
Заключение
Выполнен прогноз значений электропотребления на сутки вперёд с использованием методов прогнозирования, таких как линейная регрессия, скользящие средние и нейросети. Выявлено, что ретроспективные данные об электропотреблении не подчиняются нормальному закону распределения. По этой причине качество полученных прогнозных решений является неудовлетворительным.
С целью уменьшения ошибки прогноза выполнена процедура кластеризации с учетом фактора, влияющего на процесс потребления электроэнергии, а именно «Будний или праздничный/выходной день». Значения величин ошибок, полученные при прогнозировании с применением кластеризации, указывают на эффективность проведённой корректировки. Наименьшая величина средней абсолютной ошибки прогноза достигнута с помощью метода простой скользящей средней, которая с применением кластерного подхода равняется 1,6 % («Будние дни») и 1,5 % («Праздничные/выходные дни»). При этом до использования кластеризации средняя ошибка прогноза принимала значение, равное 2,1 %.
Проверка с помощью критерия Колмогорова – Смирнова позволила сделать вывод о том, что проведённая процедура кластеризации по будним и праздничным/выходным дням позволяет, в частности, избавиться от выбросов параметров в данных и, как следствие, повысить качество получаемых прогнозных решений.
Детальный анализ значений ошибки прогноза на часах, являющихся участками перелома, позволил зафиксировать частичное снижение средней ошибки прогнозных решений, но проблема низкого качества при этом осталась на 9-м, 13-м часах и на интервале с 17-го по 18-й часы, что говорит о необходимости использования других методов и подходов в прогнозировании.



