В настоящее время, как показывает опыт европейских стран, перспективным направлением развития атомной энергетики являются АЭС на базе газовых реакторов, выполненных из предварительно напряженного железобетона [6]. При этом сам корпус, как правило, имеющий цилиндрическую или сферическую форму, воспринимает как внутреннее давление, так и температурные и радиационные воздействия, совмещая таким образом в себе функции биологической защиты. По сравнению с металлическими, железобетонные КВД характеризуются повышенной надежностью, однако технология их изготовления весьма сложна и требует для создания предварительных напряжений применения домкратов с усилием более 1000 тонн.
В настоящей работе рассматривается методика определения напряженно-деформированного состояния (НДС) корпусов высокого давления с учетом силовых, температурных и радиационных воздействий на примере сферического КВД. Такие конструкции обладают исключительно высокими показателями трещиностойкости и пределами упругой работы. Напряженно-деформированное состояние сферических КВД характеризуется большей однородностью по сравнению с цилиндрическими аналогами [6]. Все это обуславливает повышенную надежность и безопасность. Расчетная схема сферического КВД приведена на рис. 1.
Физико-механические характеристики материала корпуса являются функциями от температуры T, а также флюенса (интегрального потока) нейтронов, поэтому определению НДС корпуса предшествует расчет распределения температурного поля и флюенса нейтронов Ф. Температурное поле определяется из уравнения теплопроводности Фурье:
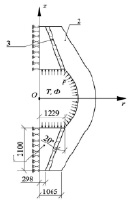
Рис. 1. Расчетная схема сферического КВД: 1 – торцевые элементы; 2 – стенка; 3 – слои, моделирующие шпонки
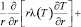
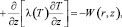(1)
где (T) – коэффициент теплопроводности; W(r, z) – плотность внутренних источников тепловыделений.
Для определения флюенса нейтронов используется диффузионное приближение:
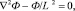(2)
где L – длина диффузии;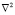 
– дифференциальный оператор Лапласа.
Целью исследования является изучение влияние косвенной (наведенной) неоднородности материала на напряженно-деформированное состояние корпуса высокого давления.
Материалы и методы исследования
Уравнения (1) и (2) решаются при помощи МКЭ. Методика определения температурного поля с учетом зависимости коэффициента теплопроводности от температуры приводится в работе [1]. Зная распределение температуры и флюенса нейтронов, можно определить, как изменяется модуль упругости бетона в толще конструкции. Зависимость Е(Т, Ф) можно записать в виде
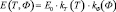, (3)
где Е0 – модуль упругости необлученного бетона при нормальной температуре; kT – коэффициент влияния температуры; kФ – коэффициент влияния радиационного облучения.
Данные по температурной зависимости модуля упругости бетона имеются в нормативной литературе [5]. Для жаростойких бетонов на портландцементе с андезитовыми, диоритовыми, базальтовыми или диабазовыми заполнителями (состав № 2 по табл. 5.1 [5]) аппроксимирующая функция kT(Т) имеет вид
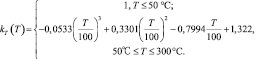(4)
Коэффициент kФ вычисляется следующим образом [3]:
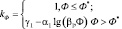(5)
где α1, β1, γ1 – эмпирические параметры, зависящие от класса бетона и его состава; Ф* – пороговое значение флюенса, определяемое из условия:
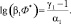(6)
Радиационные деформации определяются следующим образом:
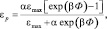(7)
где εmax – максимальная радиационная деформация, зависящая от состава бетона; Ф – флюенс (интегральный поток) нейтронов; α и β – эмпирические константы, зависящие от энергетического спектра нейтронов и вида заполнителя.
Задача решается в осесимметричной постановке. Связь между напряжениями и деформациями с учетом вынужденных деформаций имеет вид
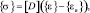(8)
где [D] – матрица упругих характеристик; {σ} = {σr σz σ θ τ rz} – вектор напряжений;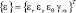 
– вектор полных деформаций; 
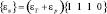– вектор вынужденных деформаций.
Для изотропного материала матрица [D] имеет вид
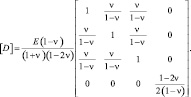(9)
Согласно вариационному принципу Лагранжа, решение уравнений теории упругости соответствует минимуму функционала полной энергии системы [4]:
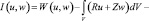
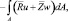(10)
где R, Z – объемные силы;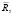 
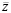– поверхностные нагрузки; W (u, w) – потенциальная энергия деформации, которая вычисляется следующим образом:
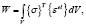(11)
где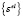 
– вектор упругих деформаций, представляющих разность между полными деформациями и вынужденными деформациями:
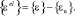(12)
Связь между полными деформациями и перемещениями имеет вид:
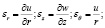
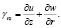(13)
Поле перемещений аппроксимируется следующим образом:
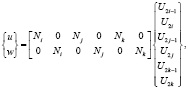(14)
где Ni, Nj, Nk – функции формы;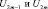 
– соответственно перемещения узла с номером m по r и z.
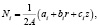(15)
где A – площадь элемента;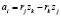 
; 
; 
.
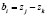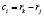Выражения для функций Nj и Nk, а также коэффициентов aj, bj, cj, ak, bk, ck можно получить циклической заменой индексов.
В результате минимизации полной энергии, задача сводится к системе линейных уравнений:
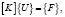(15)
где [K] – глобальная матрица жесткости; {F} – глобальный вектор нагрузки; {U} – вектор узловых перемещений.
Расчет корпуса высокого давления выполнялся при следующих исходных данных: ????0 = 3·104 МПа, v = 0,2, внутреннее давление pa = 10 МПа, температура у внутренней поверхности корпуса Тa = 100 °С, температура у внешней поверхности Тb = 20 °С, флюенс нейтронов у внутренней поверхности Фa = 4?1024 нейтрон/м2, у внешней поверхности Фb = 0, длина дифффузии L = 0,16 м, коэффициент линейного температурного расширения α = 9,1?10–6 1/ °С, коэффициент теплопроводности λ = 1,51 Вт/(м?К).
Результаты исследования и их обсуждение
На рис. 2–4 представлены соответственно графики распределения в зависимости от r и z напряжений σr, σθ, σz,. Закрашенным поверхностям соответствует решение для однородного материала, а сетчатым поверхностям – для неоднородного.
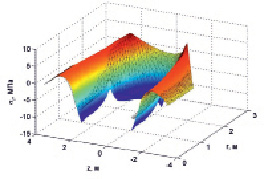
Рис. 2. Распределение напряжений σr
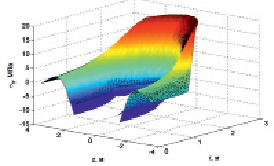
Рис. 3. Распределение напряжений σθ
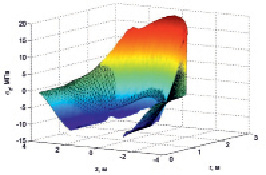
Рис. 4. Распределение напряжений σz
Из представленных графиков видно, что учет неоднородности материала приводит к существенному снижению напряжений у внутренней поверхности корпуса за счет уменьшения модуля упругости в результате температурных и радиационных воздействий. Касательные напряжения при учете неоднородности практически не изменились.
Средняя часть стенки сферического КВД находится в условиях центрально-симметричной задачи теории упругости. При наличии центральной симметрии задача сводится к дифференциальному уравнению второго порядка относительно радиальных напряжений [2]:
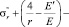
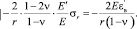(14)
Штрихом в уравнении (14) обозначена производная по радиусу.
Граничные условия для данного уравнения имеют вид
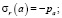
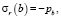(15)
где a и b – соответственно внутренний и внешний радиус сферы; pa и pb – внутреннее и внешнее давление.
Напряжения σθ можно определить из уравнения равновесия:
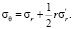(16)
Уравнение (14) было решено методом конечных разностей (МКР). На рис. 5 сплошной линии соответствует распределение напряжений σθ в средней части стенки КВД, полученное при помощи МКР, а штриховой – при помощи МКЭ. Результаты практически совпадают, что свидетельствует о их достоверности.
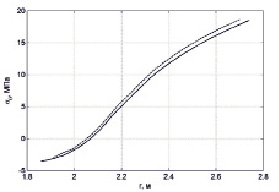
Рис. 5. Распределение напряжений σθ в средней части стенки КВД: сплошная линия – решение при помощи МКР, а штриховая – при помощи МКЭ
Выводы
Рассмотренный пример расчёта показывает, что анализ влияния неоднородности материала на напряженно-деформированное состояние конструкции должен проводиться комплексно и учитывать все возможные факторы. Из представленных результатов следует, что как растягивающие, так и сжимающие напряжения по абсолютной величине значительно превышают расчетные сопротивления бетона. Данное обстоятельство следует учитывать при назначении схем армирования конструкций.