Обучение школьников решению задач математики и информатики остается одним из главных вопросов этих предметных методик. Зачастую даже способные учащиеся испытывают трудности в поиске способа решения задачи, зная необходимый для этого учебный материал. Поэтому для каждого учителя важно найти методы и приемы обучения решению задач.
По своему назначению задачи могут быть направлены на получение знаний, отработку умений или на оценивание результатов обучения. При обучении задачи выполняют обучающую, воспитывающую, развивающую и контролирующую функции. Они развивают у школьников логическое мышление, формируют практические навыки, пространственное представление, а также эвристические умения, необходимые для творческой деятельности.
Например, происходящие изменения в развитии общества влияют и на содержание текстовых, сюжетных и практических задач, представленных в школьных учебниках. В современных учебниках содержание задач направлено на развитие научных взглядов, воспитание патриотизма и высокой морали. Однако воспитывающее значение имеет не только содержание задачи, но и методика обучения их решению. Методически продуманное обучение решению задач способствует формированию у учащихся культуры устной речи, упорства, терпеливости, воспитанию у них личностных качеств, таких как умение преодолевать трудности и достигать намеченного результата [3].
Задачи не только исполняют роль источника учебной информации, но становятся активным инструментом управления познавательной деятельностью школьников. С изменением места и роли задач в обучении математике и информатике обновляются и задачи. Авторы современных учебников чаще используют фразы «обосновать ...», «исследовать...», «сравнить..», «оценить..», «предложить другой путь решения...», «выбрать оптимальный способ...», вместо «вычислить», «построить», «найти» и т.д. [6].
В литературе, посвященной методикам обучения математике и информатике, выделяют четыре основных этапа работы над задачами [1, 2, 3]:
I. Провести анализ текста, условия задачи. Целью этого этапа является выделение объективного содержания задачи, условия и заключения, создание чертежа, схемы.
II. Осуществить поиск способа решения и составить план. На этом этапе задачу подводят под известный тип, выбирают наиболее оптимальный при заданных условиях метод решения.
III. Реализовать план решения задачи – что составляет процесс решения. Проводится практическое исполнение плана решения во всех его деталях, одновременно ведется корректировка, через соотнесение условия задачи и выбранного метода, осуществляется выбор способа по оформлению решения и записи результата.
IV. Проверить правильность решения задачи и запись ответа. На этом этапе критически анализируется полученный результат, осуществляется поиск рациональных путей решения, проводится исследование частных и особых случаев (проверка на единственность и существование решения). Также этап предполагает обобщение и систематизацию полученных в ходе работы над задачей новых знаний и опыта.
В учебном процессе рассмотренные этапы переплетаются, и при работе над задачей можно многократно возвращаться к предшествующим этапам. Учителю важно воспитывать у школьников потребность в следовании и выполнении всех четырех этапов.
Одной из интересных – с точки зрения наглядности – разновидностей математических задач являются задачи на оперирование графами, называемые задачами на графы. При решении подобных задач часто важен визуальный анализ поиска решений [5]. В данной статье рассмотрим использование графов в качестве некоторого вспомогательного средства, позволяющего облегчить процесс обучения школьников решению задач.
Компьютерные технологии позволяют усилить визуальное представление графов и помогают повысить уровень представления наглядности. Графическое представление в компьютерной среде можно получить с помощью компьютерных программ обработки графов. Среди программ визуализации графов есть более простые и более сложные, работающие онлайн и устанавливаемые на компьютер, более совершенные и находящиеся на ранних стадиях разработки, проприетарные и открытые, платные и бесплатные. У всех есть свои плюсы и минусы, специализация и спектр возможностей. Наш выбор – программа «Графоанализатор», бесплатное интерактивное приложение по созданию графов. Интуитивно понятный интерфейс, специальных навыков не требует, набор возможностей, стандартный для такого типа программ. С другой стороны, когда нужен быстрый результат, он может быть полезен: возможность подбирать цветовые схемы, динамическая демонстрация решения. Можно создавать динамичный граф, в котором изменять числовые исходные данные, с сохранением всего алгоритма построения, просматривать и работать с ним. В визуальной среде Графоанализатора школьник свободно может редактировать изображение графа, что дает возможность исследования и повышает качество обучения решению задач.
Работая в визуальной среде, школьники могут влиять на свой собственный процесс обучения. Как отмечают в своей работе Е.Ы. Бидайбеков, В.В. Гриншкун, С.Г. Григорьев применение компьютерных технологий «… стимулирует когнитивные аспекты обучения, такие как восприятие и осознание информации; способствует развитию более глубокого подхода к обучению и, следовательно, влечет формирование более глубокого понимания изучаемого материала»[4, С. 30].
Рассмотрим реализацию обучения решению задач, на основе поэтапной работы над задачей. На первом этапе работы над задачей на графы, важно суметь проанализировать и закодировать условия задачи. Создание схематической записи – второй этап – предусматривает геометрическое представление графа, как множества вершин и ребер. На этом этапе важен элемент творчества, потому что требуется найти соответствие между элементами условия и соответствующими элементами графа, а найти их будет очень не просто.
Поиск способа решения и его осуществление (с проверкой и исследованием) на третьем этапе, пробуждают и активизируют умственные способности учащихся: абстрагирование, моделирование, применение всех известных математических способов решения. На завершающем, четвертом этапе при формулировании ответа задачи также необходимо умение кодирования и абстрагирования.
Облегчение для восприятия и усвоения учащимися математических знаний может быть достигнуто использованием программы визуализации графов.
Задача 1.
Построены дороги между населёнными пунктами A, B, C, D, E, F , в таблице (рис. 1) указана их протяжённость. Если прямой дороги между пунктами нет, число в таблице отсутствует. Какова длина кратчайшего пути между пунктами A и F, если передвигаться можно только по построенным дорогам.
Решение.
1. Известно, (данные таблицы), что не все населенные пункты соединены дорогами (данные таблицы), требуется найти кратчайший путь между указанными пунктами.
2. Составление плана решения задачи начнем с чертежа. Построим граф, в котором обозначим населенные пункты точками (вершины графа). Соединим точки там, где пункты соединены дорогой (рис. 2). Из пункта (вершины) А в пункт F нарисуем путь.
Вопрос: по данным чертежа, сколько возможно вариантов перемещений? Как определить кратчайший путь?
3. Рассуждения следует начать с пункта F – конца пути. В него идет только дорога из пункта Е.
В пункт Е ведут дороги из пунктов B, C и D.
В пункт B ведет дорога из пункта A, в пункт С ведет дорога из пункта В, в пункт D ведет дорога из пункта B.
В пункт В ведет дорога из пункта А. Видим, что из пункта А в пункт F ведут 3 пути.
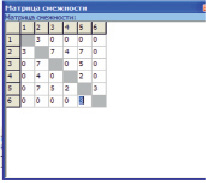
Рис. 1
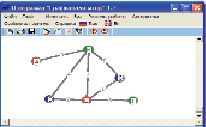
Рис. 2
Надо найти кратчайший путь из трех. Добавим в граф значение расстояний между пунктами
1-й путь: A – B – E – F = 3 + 7 + 3 = 13
2-й путь: A − B − C − E − F = 3 + 7 + 5 + 3 = 18
3-й путь: A − B − D − E − F = 3 + 4 + 2 + 3 = 12
Длина кратчайшего пути:
A − B − D − E − F = 12.
4. Для этапа проверки ограничимся ответом на вопрос: есть ли другие способы решения задачи?
Задача 2.
На рисунке (рис. 3) – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л?
Решение.
1. По заданному рисунку видно, что из пункта А в пункт Л ведет много дорог, требуется найти количество различных путей из пункта А в пункт Л.
2. Построим граф, нарисуем путь из пункта А в пункт Л.
3. Рассуждения начнем с конца, с пункта Л. К нему ведут дороги из И, Ж, К.
На рисунке (рис. 3) – города А, Б, В, Г, Д, Е, Ж, И, К, Л и схема дорог между ними.
Стрелкой указано направление, как можно двигаться по каждой дороге. Сколькими путями можно добраться из города А в город Л?
Решение.
1. По заданному рисунку видно, что из города А в город Л ведет много дорог, требуется найти количество различных путей из города А в город Л.
2. Построим граф, нарисуем путь из города А в город Л.
3. Рассуждения начнем с конца, с города Л. К нему ведут дороги из городов И, Ж, К.
В город И ведет дорога из города Д.
В город Ж ведут дороги из городов Д, В, Е.
В город К ведет дорога из города Е (рис. 4).
В город Д ведут дороги из городов Б и В.
В город В ведут дороги из городов Б, А, Г.
В город Е ведет дорога из города Г (рис. 5)
В итоге путь из города А в город Л выглядит на рис. 6.
Требуется посчитать, сколько раз А получилось. Из города А идет свой маршрут. На рисунке 13 различных путей.
4. Вопрос: встречали ли раньше подобную задачу? Если учащиеся встречали ранее подобную задачу, то составление плана решения не вызывает трудностей. Если составление плана слишком затруднено, то можно решить часть задачи. Разделив сложную задачу на простые задачи, можно облегчить процесс составления плана решения задачи.
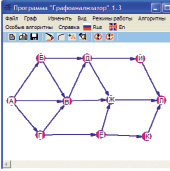
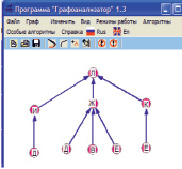
Рис. 3 Рис. 4
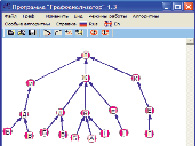
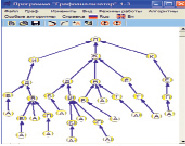
Рис. 5 Рис. 6
В поиске решения задачи самым сложным является установить последовательность (цепочку следований), которая ведет к решению.
Чтобы научить школьников устанавливать такие последовательности и рассуждать, следует у них развивать навыки мышления, помогающие им разрозненные факты выстроить в логической взаимосвязи.
Умение школьников решать задачи тесно связано с умением изложить свое решение кратко и точно. Учащиеся же при комментировании своего решения, рассказ сводят к деталям, уточнениям, которые зачастую не являются важными для обоснования решения задачи.
Немаловажную роль играет и оформление записи решения задачи, которая должна быть наглядной. При словесном или символическом оформлении решения задачи учащимся трудно увидеть ход решения, последовательность совершенных действий, соединяющих все промежуточные решения в логически завершенное целое решение. Видение в развитии хода решения представляется важным для формирования у учащихся абстрактного мышления и воображения.
Учителю важно научить ученика видеть весь ход решения задачи, сформировать у него представление о взаимосвязи между условием задачи и ее результатом и понимание этой связи.
Многие задачи школьного курса математики и информатики могут быть решены, кроме общепринятого способа, еще и с помощью понятий теории графов. Кроме того, первоначальные понятия теории графов помогают школьникам в поиске способа решения задач, как программных, так и повышенной трудности. Соблюдение учащимися определенной точности и аккуратности при построении графов имеет важное воспитательное значение, а отсутствие необходимой наглядности при решении задач является основным тормозом к осознанным мыслительным действиям.
Рассмотренный прием обучения с использованием компьютерной программы Графопостроитель, позволяет визуализировать процесс решения таких задач, представив их пошаговое решение. Метод компьютерной визуализации помогает найти путь решения, также позволяет продемонстрировать школьникам возможности современных информационных технологий, стимулирует их творческую и поисковую деятельность.



