Традиционно практические занятия по математике в вузе строятся следующим образом: в начале занятия в процессе фронтальной беседы вспоминается необходимый теоретический материал, полученный на лекции, затем преподаватель записывает номера заданий из какого-нибудь задачника по математике, соответствующих изучаемой теме, и студенты, выходя к доске или работая самостоятельно, выполняют эти задания. В конце занятия выдается домашнее задание и, если остается время, проводится небольшая проверочная работа по изученному материалу, а после изучения целого раздела обучающиеся выполняют контрольную работу.
Подобная организация учебного процесса на практическом занятии имеет ряд недостатков. Во-первых, невозможно в течение одного занятия вызвать к доске даже половину группы, и получается, что пока одни студенты работают у доски, другие в это время, чаще всего, занимаются механическим переписыванием решения задач. Фактически, в ходе практического занятия не осуществляется непрерывная обратная связь между преподавателем и всей группой. Во-вторых, оформление решений задач студентами, которые пытаются работать самостоятельно, продвигаясь в собственном темпе, зачастую оставляют желать лучшего. В-третьих, первокурсники, чаще всего, не видят связи между предлагаемыми заданиями, не осознают общий ход рассуждений и т.д.
Для оперативной диагностики нужны учебные материалы с печатной основой, включающие эти задания. Таким средством, обеспечивающим организацию активной познавательной деятельности обучаемых, отражающим логику изучения предмета и диагностику усвоения, может выступать рабочая тетрадь по конкретной учебной дисциплине.
Цель исследования: выделить и описать основные этапы конструирования рабочей тетради как содержательной основы по математике и как средства учебно-профессиональной адаптации первокурсников.
Методы исследования: анализ и синтез данных психолого-педагогической и методической литературы по проблеме исследования; обобщение, систематизация; наблюдение, опросные методы, педагогическая диагностика, педагогический эксперимент.
Результаты исследования и их обсуждение
Цель разработанной нами рабочей тетради, как дидактического средства, состоит в оказании помощи студентам при изучении математики и снижении трудностей в процессе ее изучения; в формировании функционально-графической культуры студентов и полноценного освоения всех компонентов содержания математики, общелогических методов познания и специфических методов науки, что, тем самым, должно способствовать адаптации первокурсников к обучению в вузе в организационном и содержательном плане.
В соответствии с системным подходом в основу отбора учебного материала должны быть положены принципы целостности, полноты и соответствия структуре усваиваемых знаний. Учебный материал в каждой работе должен быть представлен в виде подсистемы усваиваемых знаний, что позволит студенту выделять элементы содержания, устанавливать связи между ними, понимать логику выстраивания учебного материала, приводить знания в систему, устанавливать сферу их применения. Тем самым рабочая тетрадь должна обеспечивать названные условия адаптации первокурсников к изучению учебной дисциплины.
Согласно деятельностному подходу [1] построение учебного материала в рабочей тетради должно способствовать включению каждого студента в учебную деятельность на практическом занятии по учебной дисциплине. Мы разделяем мнение Е.Н. Перевощиковой [2, с. 217–219], что каждый новый учебный элемент должен быть представлен в тетради в соответствии с основными этапами его усвоения: актуализация (повторение теоретического материала лекции); выполнение новых действий с изучаемым объектом, их распознавание, осмысление и закрепление; применение знаний, полученных на лекции, в знакомой по обучению или новой ситуации, их обобщение и систематизация. Для этого в работах следует выделять группы заданий, построенных в соответствии со структурой учебной деятельности (мотивационно-ориентировочная, теоретическая и рефлексивно-оценочная части).
Перечисленные требования направлены на обеспечение осознанного усвоения студентами функциональных понятий в курсе математики, осмысления изученного с помощью специальной системы заданий, что является одним из важных условий учебно-профессиональной адаптации первокурсников [4].
С учетом деятельностного подхода к построению рабочей тетради по математике каждая ее работа должна представлять своего рода канву практического занятия.
В русле личностно ориентированного подхода рабочая тетрадь должна обеспечивать полноценную работу студента как на практическом занятии, так и при выполнении домашнего задания. В нее должны быть включены задания, способствующие осознанию смысла и значимости изучаемых дидактических единиц для развития личности студента.
Важным условием адаптации первокурсников является осуществление оперативной диагностики, обеспечивающей внесение своевременных коррективов в процесс обучения, формирование действий самоконтроля и взаимоконтроля, самооценки, рефлексии выполненных действий. Для обеспечения этого условия в тетрадь должны быть включены диагностические задания, способствующие формированию этих действий. Нужны упражнения, позволяющие увеличить долю самостоятельной работы студента с опорой на готовые образцы рассуждений и формы записи решений, а также задания, позволяющие проверить решения с помощью ответов и организовать как индивидуальную работу на занятии, так и работу в парах.
В аспекте гуманистического, гуманитарного и культуросообразного подходов рабочая тетрадь должна стать собственностью студента, его дидактическим средством. В нее должны быть включены задания, способствующие формированию функционально-графической культуры, грамотной математической речи, что является еще одним условием учебно-профессиональной адаптации первокурсников. Также в рабочую тетрадь должны быть включены демонстрационные проверочные задания, снабженные ответами, которые обеспечивают условия для самоконтроля и выступают в качестве самой гуманной формы контроля. Рабочая тетрадь должна способствовать усвоению «знаний о знании», овладению средствами и методами познания и, в целом, адаптации первокурсников к обучению в вузе в организационном и содержательном плане.
Поскольку основной единицей каждой работы в рабочей тетради является упражнение (задание), то при построении учебного материала в виде упражнений в тетради мы учитывали общедидактические принципы конструирования системы упражнений (полноты; однотипности; наглядности; сравнения; преемственности; непрерывного повторения; вариативности; фундаментальности; целенаправленности и адаптивности) [2, 3].
Выделим и конкретизируем требования к представлению учебного материала в рабочей тетради в виде упражнений.
1. Наличие в рабочей тетради упражнений, позволяющих актуализировать прошлый опыт студентов, организовать повторение учебного материала из школьного курса математики и полученного на лекции.
Методика работы с такими упражнениями предполагает следующую совместную деятельность преподавателя и студентов: установка преподавателя о необходимости выполнения указанных им заданий для того, чтобы студенты вспомнили необходимые сведения из школьного курса «Алгебры и начал анализа» и материал, полученный ранее на лекции; выполнение указанных заданий в рабочей тетради; обсуждение полученных результатов, с точки зрения новизны и значимости действий, выполненных студентами; необходимая коррекция.
Это требование соблюдено нами при построении всех работ в рабочих тетрадях «Функции. Свойства функций» [5].
2. Наличие в рабочей тетради заданий, позволяющих включать студентов в деятельность по «открытию» нового приема, способа решения, по формулировке учебных задач практического занятия.
Например, в работу «Модуль вещественного числа» [5] включены задания, позволяющие студентам «открыть» и сравнить два способа построения графиков функции, содержащих модуль.
3. Наличие работ, позволяющих обобщать и систематизировать усвоенные в школе знания, раскрывать смысл важных понятий курса математического анализа, в том числе не входящих в программу общеобразовательного курса школьной математики.
Анализ ФГОС для общеобразовательной школы и учебников по математике показал, что понятия «обратная функция», «композиция функций», «обратные тригонометрические функции», на базе которых строится изучение многих понятий математического анализа в вузе, не входят в программу общеобразовательного курса. Поэтому в рабочую тетрадь включена работа, позволяющая систематизировать и обобщить функционально-графические знания и умения студентов и раскрыть смысл понятий «обратная функция» и «композиция функций». Наиболее эффективной формой представления этих понятий является их графическая модель, анализ и изучение которой позволяют студентам перейти к аналитической модели (т.е. от наглядно-иллюстративного уровня к операционному и затем формально-логическому) и сформулировать формально-логические определения.
4. Наличие в рабочей тетради упражнений, направленных на осознанное усвоение определений, содержащих кванторы.
Такие свойства функций, как ограниченность, непрерывность, множество значений функции рассматриваются в школе на наглядно-иллюстративном и операционном уровне, но не определяются на формально-логическом языке. Определения этих понятий содержат кванторы, связаны с понятием предела функции и, как правило, очень плохо усваиваются студентами. Поэтому в рабочую тетрадь включены задания, направленные на осознанное усвоение определений понятий такого вида (с одним и двумя кванторами).
5. Наличие к заданиям работы рекомендаций, указаний, образцов рассуждений, обеспечивающих переход от теоретических фактов к их применению в конкретных задачах.
Это требование соблюдено при построении всех работ в созданных нами рабочих тетрадях. Рекомендации, образцы рассуждений способствуют формированию умения студентов обоснованно выполнять свои действия, правильно оформлять решения задач.
6. Наличие заданий, направленных на формирование грамотной математической речи.
При выполнении таких заданий целесообразно использовать прием комментированного письма, который позволяет не только проверить правильность заполнения пропусков, таблиц и схем в рабочей тетради, но и развивать речевую культуру первокурсников. Это требование реализуется при выполнении заданий на заполнение схем, таблиц, пропусков в определениях понятий, формулировках теорем, свойств и т.п.
7. Наличие текстов задач и заданий, необходимых рисунков и записей, позволяющих студентам соединять моторную деятельность и зрительное восприятие, экономить время на занятии, создавать условия для развития мыслительных операций (анализ, синтез, сравнение и т.п.), для организации поисковой деятельности обучаемых на практическом занятии.
8. Включение в рабочую тетрадь групп заданий, обеспечивающих поэтапное формирование умений.
Каждое из таких заданий направлено на освоение вполне определенных действий. Последовательное выполнение этих заданий позволяет студенту выделить все необходимые шаги при решении более сложной задачи. Например, в работе № 5 «Композиция функций. Обратная функция» [5] при выполнении задания № 16 студенты анализируют процесс нахождения функции обратной для функции f(x) = 3x + 1, выделяют последовательно все этапы данного действия, заполняя пропуски, а также выясняют взаимное расположение графиков прямой и обратной функции. Далее в задании № 17 они выполняют все выделенные выше этапы самостоятельно для функций y = x2, x ≤ 0 и y = 1 + log2(x + 2), строят графики указанных функций и обратных им. В следующем задании (№ 18) студентам уже нужно найти обратную для кусочной функции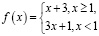 
и построить ее график в одной системе координат с графиком исходной функции.
9. Наличие работ, которые можно использовать для самостоятельного изучения некоторых тем, построенных на основе целесообразно подобранных упражнений, соответствующих логике изложения материала.
В качестве примера такой работы можно назвать работу № 2 по теме «Ограниченные и неограниченные функции. Наибольшее и наименьшее значения функции. Точные границы функции» [5]. Ей предшествует работа «Ограниченные и неограниченные множества. Точные верхняя и нижняя границы множества. Наибольший и наименьший элементы множества», на основе выполнения которой студенты могут самостоятельно выполнить задания по указанной теме, используя знания и умения, полученные ранее, применяя такие методы познания, как аналогия, обобщение, анализ и синтез.
10. Включение в рабочую тетрадь ключевых задач темы.
Это задание ориентирует студентов на актуализацию школьных знаний. Результаты его выполнения позволяют выделить тех студентов, которые не освоили в школе выделенных приемов и нуждаются в адресной помощи.
11. Наличие в рабочей тетради заданий для формирования у студентов действий самоконтроля и самооценки, способности к рефлексии (осознанию выполненных действий).
Задания для самооценки и самоконтроля представлены в рабочей тетради в виде диагностических заданий (ТДО – текущая диагностика обучающего характера, КД – контрольная диагностика) и в виде итоговых тестов для самопроверки усвоения всего учебного модуля.
В основу деления по уровням сложности задач положено наличие или отсутствие алгоритма решения. Так, задания, отмеченные цифрой I в работе КД, соответствуют базовому уровню, и верный результат характеризуется оценкой «удовлетворительно». Задания, отмеченные цифрой II, соответствуют повышенному уровню, и верный результат их выполнения характеризуется оценкой «хорошо», а задания, отмеченные цифрой III,– высокому уровню, что соответствует оценке «отлично». В русле идей адаптивного обучения студент может начинать работу с любого уровня, постепенно переходя к более сложному или более простому заданию.
Отметим, что рабочая тетрадь должна строиться в соответствии с задачами адаптации, с принципами построения системы упражнений для каждого этапа усвоения, построение каждой работы отражает план занятия и план учебно-познавательной деятельности первокурсников.
Особое внимание при разработке рабочей тетради уделяется системе упражнений по формированию умений и навыков, удовлетворяющей дидактическим требованиям. Важной отличительной особенностью построенной системы упражнений стало включение в нее заданий, адекватных действиям, лежащим в основе усвоения новых знаний. Сюда вошли задания на распознавание нового математического объекта, на осмысление действий с ним, на выведение следствий и подведение под понятие, на установление связей между новыми и изученными ранее понятиями (например, такими, как производная и первообразная функции), на работу с определениями понятий, содержащих один или два квантора. Заполнение пропусков в подобных заданиях, приведенных в рабочей тетради, помогает первокурсниками усваивать метазнания и позволяет постепенно развивать у них грамотную математическую речь путем постоянного воспроизведения вслух или «про себя» имеющихся текстов и необходимых слов, терминов, оборотов речи.
Выводы
Итак, содержание рабочей тетради по математике как средства учебно-профессиональной адаптации первокурсников к обучению в вузе должно быть выстроено таким образом, чтобы обеспечить включение каждого студента в учебную деятельность по усвоению содержания учебного материала и помочь студенту в организации самостоятельной работы по изучению математики. Для этого в созданных нами рабочих тетрадях по темам «Функции. Свойства функций», «Неопределенный интеграл» каждая работа построена в соответствии с этапами учебно-познавательной деятельности и включает три части: мотивационно-ориентировочную, теоретическую и рефлексивно-оценочную. Мотивационно-ориентировочная часть позволяет включать первокурсников в постановку целей и учебных задач занятия, актуализировать прошлый опыт студентов. Теоретическая часть направлена на формирование у первокурсников системы научных знаний, предметных и профессионально-значимых умений. Рефлексивно-оценочная часть способствует формированию самоконтроля, самооценки, рефлексии студентов, выявлению смысла выполненной работы. Содержание изучаемого материала в рабочей тетради по названным темам раскрывается через систему упражнений, адекватных формируемым действиям, выполнение которых должно способствовать не только их освоению студентами, но и помогать осмысливать общий ход рассуждений, обосновывать свои действия. Важным требованием к конструированию рабочей тетради является включение в нее заданий для диагностики, позволяющих осуществлять оперативную обратную связь, сопоставлять планируемые и достигнутые результаты.