Целью применения математических методов в дидактике является описание процессов и закономерностей обучения, выявление факторов и явлений, влияющих на процесс формирования знаний обучающегося и разработка эффективных технологий управления обучением на основе полученных результатов.
В зависимости от постановки дидактической задачи при формализации могут применяться либо аналитические зависимости, либо модели, построенные с использованием теории графов.
При описании дидактических процессов, являющихся непрерывными функциями времени, применяют аналитические зависимости, использующие, как правило, дифференциальные, вероятностные и статистические соотношения исследуемых параметров. В них оцениваемыми величинами могут являться скорость передачи, усвоения и забывания учебной информации, изменение состояния уровня обученности субъекта обучения, и т.д.
При математическом описании количество знаний обучающегося рассматривается как поток информации, циркулирующий в системе «обучающий – субъект обучения», и обычно выражается в виде интегро-дифференциальных уравнений. На их основе решается ряд практических примеров и делаются рекомендации по оптимизации процесса обучения, например, по распределению учебной нагрузки в течение заданного времени обучения.
В данной работе будут рассмотрены основные существующие на сегодняшний день подходы к формализации процесса формирования знаний и построению так называемых кривых научения (КН). На основе анализа коэффициентов, характеризующих процесс научения, входящих в аналитические зависимости предполагается выявить возможности усовершенствования существующих моделей с целью получения математической зависимости, более точно соответствующей особенностям процесса усвоения.
Рассмотрим различные эмпирические модели функции научения, которые учитывают такие параметры учебного процесса, как скорость усвоения учебного материала, забываемость и мотивацию. Необходимо отметить, что не все рассматриваемые модели в явном виде учитывают мотивацию обучающегося, поэтому при анализе они разбиты на две группы: модели без учета мотивации и модели, учитывающие мотивационную составляющую процесса научения.
Модели без учета мотивации описаны в работах Р.В. Майера, А.П. Свиридова, А.Н. Членова, П.А. Орлова, Д.А. Новикова и др.
В работе [3] процесс научения представляется как суперпозиция потоков усвоения и забывания порций учебной информации. В связи с чем скорость изменения количества знаний предлагается описывать дифференциальным уравнением
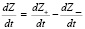, (1)
где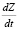 
– скорость изменения количества знаний обучающегося. Она равна разности скорости усвоения знаний 
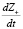и скорости забывания 
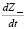. В процессе обучения учащийся усваивает всю переданную ему информацию и скорость ее поступления к нему остается постоянной ? = 
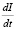= const. Скорость забывания пропорциональна количеству знаний обучающегося – 
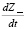= – ?Z. Тогда количество знаний учащегося в момент времени t = t0 + ? равно
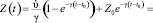
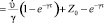. (2)
Подставляя Z0 = 0 в (2) получаем, что количество усвоенных знаний за время t = t – t0 равно 
(1 – е–??).
В работе [4] проведен обзор математических моделей итеративного научения (обучение в строго повторяющихся условиях), представленных различными авторами в разные годы. Автор отмечает, что «итеративное научение, как правило, характеризуется замедленно-асимптотическими кривыми научения (КН), аппроксимируемыми экспоненциальными кривыми». В общем виде экспоненциальная кривая описывается зависимостью
x(t) = x? + (x0 – x?) e -g t, t > 0, (3),
где t – время научения, x(t) – объем знаний в момент времени t (на n-й итерации), x0 – соответствует моменту начала научения, x? – конечное значение объема знаний (величина, к которой КН асимптотически стремится). Величина g – некоторая неотрицательная константа, характеризующая скорость научения. Она определяет скорость изменения КН. Размерность ее обратна времени обучения или числу итераций.
Далее, отмечая, что процесс итеративного обучения является частным случаем научения, он предлагает описывать его логистической кривой, которая аппроксимируется зависимостью
x (t) = x0 x? / (x0+ (x? – x0) e -?t), (4)
где x(t) – объем знаний в момент времени t, x0 –объем знаний в начальный момент времени, x? – объем знаний в конце обучения, ?– параметр, характеризующий процесс забывания. В зависимости от начального и конечного значений объема знаний можно получить либо возрастающую, либо убывающую кривую.
Вероятностный подход к моделированию процесса научения был описан у А.П. Свиридова [6] и позднее получил развитие в работах А.Н. Членова, П.А. Орлова и др. Так, в работе [9] предложена макровременная модель, охватывающая период изучения целой дисциплины или какой-либо ее части. Авторы исходят из того, что обучение как сложный психофизический процесс может быть описан аналитическими моделями, имеющими вероятностный или статистический характер. Это обеспечивает адекватность модели исходной системе за счет учета свойств и связей, не поддающихся детерминированному описанию. Ими вводятся понятия мгновенной вероятности получения знаний (Pп) и их забывания (Рз). Эти величины определяются соответственно, через плотности вероятности, получившие в работе название интенсивность. Считая случайные события получения и забывания знаний независимыми, получают временную зависимость количества усвоенных знаний:
Q (t) = [Q0 + (Q1 – Q0)(1 – e-?t)]e-?t, (5)
где Q0 – начальный объем знаний, Q1 – конечный объем знаний, ? – коэффициент, характеризующий получение знаний, ? – коэффициент, характеризующий забывание знаний.
В данной зависимости по сравнению с моделями, рассмотренными выше, где существует только параметр, характеризующий забываемость, введен параметр, определяющий интенсивность получения знаний. Показано, что учет в различии интенсивности получения и забывания знаний позволяет в неявном виде учитывать мотивацию обучающегося. Это дает возможность прогнозировать динамику усвоения знаний и разрабатывать методические рекомендации по правильному подбору и расстановке учебных дисциплин на определенный период обучения [8].
Проблемы решения задач прогнозирования состояния уровня знаний обучающегося и оптимизации процесса управления обучением вызвала необходимость введения в функцию научения еще одного параметра, описывающего процесс усвоения – мотивацию обучающегося.
Аналитические зависимости такого рода описаны Р.В. Майером, М.А. Епифановой, Е.Н. Рябиновой и некоторыми другими авторами.
Так, в работе [2] Р.В. Майер предлагает следующую имитационную модель зависимости изменения знаний от времени:
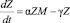, (6)
где ? и ? – коэффициенты научения и забывания ученика. Здесь мотивация (М) прямо пропорциональна разности между уровнем предъявляемых требований U и уровнем знаний Z: M = U – Z , а когда U – Z превышает некоторый предел C, мотивация исчезает (M = 0). Мотивацию обучающегося им предлагается описывать ступенчатой функцией:
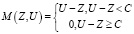. (7)
При этом скорость изменения знаний ученика определяется уравнением:
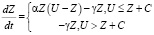. (8)
Данная модель при определении скорости изменения знаний учитывает мотивацию, но нет явной аналитической зависимости функции Z от времени, а получается только имитационная модель в конечных разностях.
Конечная аналитическая зависимость знаний от времени с учетом мотивации предложена в работе [1]. Авторы исходят из того, что мотивация как основа для самореализации присутствует у обучающего всегда и является постоянной. В роли мотивов могут выступать интересы, эмоции, идеалы и т.д. Поэтому скорость изменения знаний обучающегося с учетом эффекта мотивации предлагается описывать логистическим уравнением вида
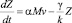, (9)
где ? – степень обучаемости учащегося, M = const – коэффициент мотивации учения, v – скорость передачи информации, 
– коэффициент уровня забывания (k > 1 при положительной мотивации и k < 1 при отрицательной мотивации). Логистическое уравнение (9) имеет аналитическое решение
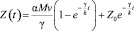. (10)
Вычисление значений Z(t) при различных величинах входящих в него параметров, позволяют определить зависимость процесса формирования учебных знаний и процесса их сохранения от степени мотивации.
Еще один подход к построению кривой научения с учетом мотивационной составляющей предложен в работах Б.А. Титова и Е.Н. Рябиновой. Так, в [7] ими описана математическая модель усвоения учебной информации, которая представлена в виде системы двенадцати дифференциальных уравнений, записанная относительно функций усвоения и мотивационных составляющих учебной информации. Система описывает зависимости между тремя потоками учебной информации –?Yj(t) – объем усвоенной учебной информации за промежуток времени ?t, ?Mj(t) – объем мотивационной составляющей учебной информации и ?Zj(t) – объем транслируемой учебной информации за тот же промежуток времени. В данной эмпирической модели под мотивационной составляющей учебного процесса понимают специальным образом представленную учебную информацию, содержащую дидактические элементы, стимулирующие учебную деятельность и способные повышать степень мотивации субъекта обучения.
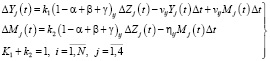. (11)
Здесь коэффициенты ?, ?, ?, ? и ? характеризуют индивидуальные особенности восприятия и усвоения учебной информации обучающимся и определяются по результатам психологического тестирования. Коэффициенты k1 и k2 определяют соотношение между объемом учебной информации, подлежащей усвоению и объемом мотивационной составляющей учебной информации.
В результате решения данной системы и анализа моделируемой ей кривой научения делается вывод о том, что процесс научения обладает свойствами насыщения и инерционности, также определяются принципы построения учебного материала, несущего в себе мотивационную составляющую.
Таким образом, видно, что, основываясь на неоднозначности определения мотивации как психологического явления, авторы получают различные математические зависимости, описывающие процесс усвоения учебной информации.
Автор данной статьи также полагает, что мотивация учащегося имеет сложный психологический характер. Она обеспечивается и поддерживается не только внешними стимулами (у Р.В. Майера это стремление преодолеть противоречие между требуемыми и имеющимися знаниями). Обучающийся также всегда имеет и внутренние побуждения, которые носят личностную окраску и являются движущей силой познания. Даже достигнув необходимого уровня знаний, он все равно остается мотивированным на обучение, то есть мотивация не может стать равной нулю. Следовательно, ступенчатая функция, предложенная Р.В. Майером для описания мотивации, не совсем точно отражает психологические механизмы этой сложной динамической системы. Для устранения этой неточности предлагается заменить ступенчатую функцию на близкую к ней, но гладкую функцию – функцию отсечения. В нашем случае она будет иметь вид
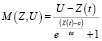, (12)
где U – уровень требований, Z(t) – объем знаний в момент времени t, С – некоторый предел уровня знаний, a – величина, отвечающая за размытость ступеньки.
В связи с чем дифференциальное уравнение скорости изменения знаний учащегося, предложенное Р.В. Майером, будет иметь вид
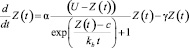, (13).
Это уравнение решается численно. Коэффициенты могут быть найдены методом наименьших квадратов по результатам тестирования учащихся.
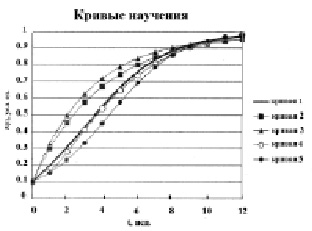
Кривые научения
Для проверки корректности зависимости, предложенной для описания мотивации, проведем сравнительный анализ всех кривых научения, рассмотренных в работе.
Графики функций научения представлены на рисунке. Для сравнения моделей коэффициенты были нормированы таким образом, чтобы значения всех функций были близки к единице при t = 12.
Решение уравнения (13) – кривая 1. Начальные условия Z (0,01) = 0,1. Значения коэффициентов U = 1, C = 0,5, kb = 0,5, ? = 0,005, ? = 1.
Расчеты по формуле (10) – кривая 2. Значения коэффициентов ? = 0,5, М = 0,5, k = 1, ? = 0,25, ? = 1, Z0 = 1.
Расчеты по формуле (5) – кривая 3. Значения коэффициентов Z0 = 0,5, Z1 = 1, ? = 0,294, ? = 0,00154.
Кривая 4 является решением системы уравнений (11), которая в несколько модифицированном виде рассмотрена авторами в работе [6]. Параметры для расчетов взяты из данной работы Т = 2,5, k = 1, km = 0,05, Tm = 10, a = 2/T, с = 1/T2, e = 1/Tm, f = km/Tm.
Расчеты по формуле (4) – кривая 5. Значения коэффициентов x0 = 0,1, x? = 1, ? = 0,5.
Анализ полученных графиков показывает, что ярко выраженных отличий в поведении кривых, описываемых предложенными зависимостями, не существует. Различия определяются в основном, наличием в уравнении коэффициента, учитывающего мотивацию. Так, например, кривые 2 и 3 близки по поведению, имеют выпуклый характер и стремятся к единице при стремлении t к бесконечности. Это объясняется тем, что в данных уравнениях мотивация либо не учитывается (5), либо остается неизменной в течение всего времени обучения (10). Значения логистической функции (4) близки по характеру к значениям функции (11), но в ее выражении отсутствуют в явном виде коэффициенты, характеризующие роль мотивации в обучении. Функция научения (13), предложенная в данной работе, совпадает по характеру поведения с функцией, описанной системой дифференциальных уравнений (11), где определение мотивационной составляющей происходит на основе учета коэффициентов, характеризующих индивидуальные особенности восприятия и усвоения учебной информации, полученных на основе экспериментальной работы с группой обучающихся [7]. Существуют области выпуклости вверх и вниз, при стремлении t к бесконечности значения функций стремятся к единице. Это позволяет сделать вывод о том, что формула (12), предложенная для описания мотивации, достаточно адекватно описывает процесс ее изменения на протяжении определенного учебного периода, следовательно, можно утверждать, что зависимость (13) корректна и является уточнением математической модели процесса усвоения, предложенной Р.В. Майером.