В последние годы целый ряд основных операций в механической обработке стали успешно выполнять промышленные роботы (фрезерование концевыми фрезами, шлифование, полирование и другие) с погрешностью обработки до 0,01 мм. Преимущества использования роботов следующие: стоимость робота в несколько раз меньше стоимости 5-координатного станка с ЧПУ; высокая маневренность (в одной роботизированной ячейке можно организовать несколько рабочих зон); гибкость функционирования (вариативность решений «инструмент к детали», «деталь к инструменту» или совместные движения инструмента и детали в процессе выполнения операции); значительно меньшая масса и потребление энергии в процессе работы.
Для автоматизированного высокоскоростного и высокопроизводительного фрезерования деталей сложной формы может быть использовано исполнительное устройство, состоящее из манипулятора инструмента и манипулятора детали [5], построенных с использованием подходов параллельной кинематики [1]. Такое решение сочетает в себе высокую жесткость и разделение движений между инструментом и обрабатываемой деталью (двухканальность управления), присущие обрабатывающим центрам, с высокой кинематической маневренностью и относительно малой массой звеньев, свойственными технологическим роботам. Кроме этого, система обладает высокой динамичностью приводов, высокой скоростью относительного перемещения детали и инструмента, стабильностью температурных параметров, высокой жесткостью за счет замыкания кинематической цепи, возможностью эффективной реализации статической разгрузки [2].
Эффективность технического функционирования рассматриваемой робототехнической системы во многом определяется эффективностью его системы управления. Задача системы управления – обеспечение согласованного перемещения инструмента и детали по запрограммированной траектории с требуемой ориентацией и заданной контурной скоростью и с погрешностями, не превышающими допустимые уровни.
На погрешности исполнительных движений робота-станка влияет целый ряд факторов. В общем случае наиболее сильное влияние могут оказывать упругость и люфты механических передач манипулятора, а также значения контурной скорости движения инструмента и кривизны обрабатываемой поверхности. В предлагаемой исполнительной системе люфты отсутствуют, а упругие деформации могут быть сведены к минимальным допустимым значениям на этапе конструирования. В работе [4] отмечается, что значительное увеличение точности механообработки обеспечивается в результате одновременного увеличения жесткости по нормали к поверхности обрабатываемого объекта и снижения до требуемого уровня жесткости «технологической пружины». Это достигается путем использования более прогрессивных структур управления, способных компенсировать упругие смещения инструмента по нормали к поверхности объекта. При этом с целью увеличения производительности необходимо стремиться к наиболее полному использованию силовых возможностей привода, предотвращая, однако, их перегрузки. Таким образом, управление осуществляется в результате одновременного использования обратных связей по контролируемым силам, которые с учетом текущей конфигурации манипулятора динамически корректируют контурную скорость и регулируют эквивалентную податливость инструмента вдоль траектории.
Исходя из отмеченных выше положений, управление обработкой в предлагаемой исполнительной системе может строиться в пространстве базовых координат с регулированием контурной скорости в функции силового взаимодействия между инструментом и заготовкой. В то же время высокая жесткость исполнительного механизма и его высокие демпфирующие возможности указывают на необходимость импедансного управления в рассматриваемом случае. Большая величина скорости резания при высокоскоростной обработке практически сглаживает пульсации сил резания от отдельной режущей кромки фрезы, и изменения сил резания могут быть лишь при изменении припуска на обработку как медленно меняющееся воздействие. Более того, при синтезе программной траектории выбираются гладкие траектории, а также стремятся к постоянству глубины резания и подаче на зуб. Учитывая сказанное выше, а также исходя из возможности формирования двухканального управляющего воздействия, управление траекторным движением рассматриваемого исполнительного устройства предлагается осуществлять позиционно-силовым способом [3], при котором одним их манипуляторов создается дозированное силовое взаимодействие между инструментом и обрабатываемым изделием, а другим осуществляется заданное относительное перемещение. Процесс перемещения инструмента и обрабатываемого изделия, с точки зрения их взаимодействия состоит из нескольких этапов: этап «свободного» движения, заключающийся в относительном перемещении инструмента и изделия до момента касания; этап врезания, при котором необходимо обеспечить плавное нарастание сил резания во – избежание поломки инструмента и этап резания с управляемым положением инструмента относительно изделия, при котором (например, при трохоидальном фрезеровании) происходит циклическое чередование этапов свободного движения и резания. Исходя из сказанного, управление движением робота-станка должно быть гибридным позиционно-силовым с переключением структуры.
На рис. 1 приведена обобщенная структура системы управления роботом-станком, содержащая подсистему стабилизации динамических характеристик, датчик силового взаимодействия, расположенный на выходном звене манипулятора инструмента, устройство управления, осуществляющее позиционное и (или) позиционно-силовое гибридное управление перемещением звеньев манипуляторов.
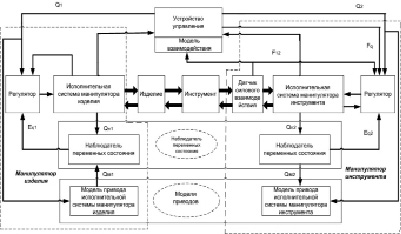
Рис. 1. Обобщенная структура системы управления роботом-станком
Задача стабилизации динамических характеристик исполнительной системы может быть ограничена обеспечением инвариантности к изменению только одного параметра – приведенного момента инерции, и она может быть решена на уровне привода без рассмотрения вопроса динамической коррекции программного движения. Этим освобождаются вычислительные ресурсы для решения задачи формообразования в процессе обработки в реальном масштабе времени, что является важным фактором при высокоскоростном резании. При решении задачи синтеза предпочтение может быть отдано методу сигнально-параметрической коррекции на основе модели системы с заданными свойствами.
Запишем уравнение движения автономного привода с регулятором тока, которое содержит момент инерции и его первую производную и имеет вид
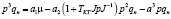. (1)
Здесь а1, а2, а3 – коэффициенты, ? – управляющий момент, ТКТ – постоянная времени контура тока, J – переменный момент инерции, p – оператор дифференцирования.
Представим выражение (1) в векторно-матричном виде относительно ошибки выходной координаты и ее производных:
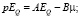
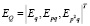. (2)
Полагая, что указанные ошибки являются отклонениями от эталонных значений, в качестве минимизирующего функционала используем квадратичную интегральную форму
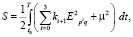(3)
где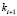 
– весовые коэффициенты.
Управляющее воздействие, доставляющее минимум выражению (3), будем формировать в виде
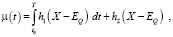(4)
где h1, h2 – коэффициенты регулятора, а Х – входное воздействие на регулятор.
В соответствии с выражениями (1) – (4) для обеспечения инвариантности динамических свойств манипуляционной системы предлагается использовать ее внутреннюю эталонную компьютерную модель с наблюдателем и сигнальной компенсацией отклонений между и объектом и моделью (рис. 2).
На рис. 2 обозначено:
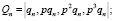
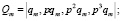
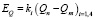
– векторы состояния привода, модели и ошибок.
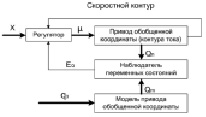
Рис. 2. Структура системы коррекции привода обобщенной координаты
Управление каждым манипулятором осуществляется в базовой системе координат. На рис. 3 приведены системы координат при реализации предлагаемого способа обработки.
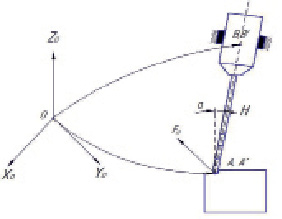
Рис. 3. Системы координат при реализации предлагаемого способа обработки
Выбранные системы координат можно связать матричным соотношением (4.16)
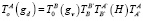(5)
Здесь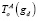 
– матрица координатных преобразований точек траектории обработки детали в базовую систему; 
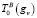– матрица координатных преобразований характеристической точки манипулятора инструмента в базовую систему; 
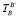– матрица упругих перемещений ирструмента; 
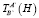– матрица координатных преобразований режущей кромки инструмента относительно т.В; 
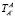– матрица составляющих погрешности обработки.
Уравнение для решения обратной задачи кинематики манипулятора изделия имеет вид
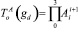. (6)
Здесь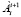 
– матрицы преобразования связанных координат в представлении Денавита-Хартенберга.
При решении обратной задачи компоненты матрицы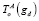 
– задаваемые величины.
Для решения обратной задачи относительно линейных скоростей необходимо продифференцировать соотношения (6) по времени и записать выражение
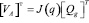, (7)
где VA – вектор линейной скорости конечной точки выходного манипулятора изделия, J(q) – матрица Якоби для преобразования скоростей, Qg – вектор обобщенных скоростей. Полагая величину VA заданной, Qg определяется с помощью обратного преобразования:
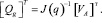(8)
При «свободном» движении задачей управления формально является сведение к единичной матрицы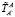 
в выражении 6 при отсутствии силового взаимодействия (нулевого сигнала с силомоментного датчика). Тогда согласованное движение манипуляторов можно описать матричными соотношениями:
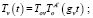
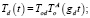
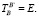
Задача управления:
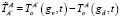, при t = tk ;
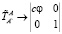4*4. (9)
Управляющие моменты определяются следующим образом:
; 
; 
;
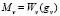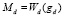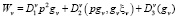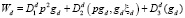. (10)
При позиционно-силовом управлении целесообразно организовать компенсацию позиционного возмущения. Управляющие моменты при этом имеют следующий вид:
;
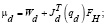
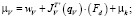
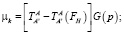
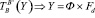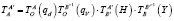. (11)
Работа выполнена при финансовой поддержке РФФИ (проект № 13-08-01364).