Введение в Российской Федерации новых образовательных стандартов высшего образования определило основную цель образовательного процесса – формирование у обучаемых поведенческой модели, подразумевающей способность анализировать бакалавром возникающую задачу и определять требуемые для ее решения технические средства [6]. В учебном процессе вуза данная модель реализуется компетенциями, ориентированными на работу с информацией и моделированием процессов, что дает возможность осуществлять также и разнообразную и детальную интерпретацию получаемой информации, а следовательно, гарантировать более глубокое понимание и усвоение материала.
Цель статьи – анализ возможности применения информационных технологий при формировании поведенческой модели с использованием информационных технологий на примере разработки модуля «Адаптивные антенные решетки» в курсе дисциплины «Устройства СВЧ и антенны» по направлению обучения 11.03.01 Радиотехника.
Актуальность выбранной темы модуля обусловлена тем, что в условиях резкого роста используемых радиотехнических систем и вследствие этого существенного усложнения радиотехнической установки одним из способов обеспечения устойчивого функционирования подвижных систем связи являются адаптивные антенные решетки, позволяющие осуществлять динамическую подстройку диаграммы направленности в реальном режиме времени.
Возможные направления использования информационных технологий в модуле
Выполним анализ возможных направлений применения информационных технологий при реализации обучающего модуля «Адаптивные антенные решетки».
Как известно, например, из [4], структурная схема адаптивной антенны наряду с излучателями и диаграммообразующей схемы должна включать адаптивный процессор для вычисления вектора весовых коэффициентов, обеспечивающих формирование главного лепестка в направлении полезного сигнала и «нулей» в направлении помеховых сигналов при использовании алгоритма либо оптимального, либо адаптивного типов. Поскольку случай, когда направления прихода сигналов являются неизвестными, то при построении модуля целесообразно рассматривать адаптивные алгоритмы, осуществляющие расчет вектора весовых коэффициентов путем статистической обработки накопленных выборок, т.е. за период так называемого переходного процесса. Данный процесс, называемый также обучением устройства обработки, начинается с обнаружения сигналов и заканчивается в момент нахождения оптимального решения, т.е. когда отношение «сигнал/шум» на выходе антенны достигает максимального значения. Следует отметить, что наблюдаемые в переходный период процессы определяют качество функционирования адаптивной антенны, т.е. глубину и скорость формируемых «нулей» диаграммы направленности.
На длительность переходного процесса оказывают существенное влияние параметры алгоритма адаптации. В приведенной в работе [2] классификации алгоритмов управления к адаптивным алгоритмам относятся алгоритмы прямого решения (непосредственного обращения матрицы, рекурсивного обращения матрицы, последовательной декорреляции) и рекурсивные (градиентные и Хауэлса-Аппельбаума). Каждый из перечисленных выше типов алгоритмов имеет свои достоинства. Так, алгоритм рекурсивного обращения матрицы, описанный в [1], обеспечивает упрощение схемы процессора, а, следовательно, и уменьшение вычислительных затрат при нахождении вектора весовых коэффициентов. С точки зрения простоты и наглядности построения модуля, что необходимо обеспечить в учебном процессе, целесо образно использовать рекурсивный алгоритм Хауэлса-Аппельбаума. Достоинствами данного алгоритма, как известно из теории, приведенной, например, в [4], являются относительная простота ее технической реализации, способность к самокоррекции промежуточных ошибок вычислений, возможность максимизации отношения «сигнал/шум» в предположении о том, что направление прихода полезного сигнала известно, однако сам сигнал в течение большей части времени приема может отсутствовать.
Модель алгоритма Хауэлса-Аппельбаума
Функциональная схема адаптивной антенной решетки из N элементов с контуром Хауэса-Аппельбаума из работы [4] приведена на рис. 1.
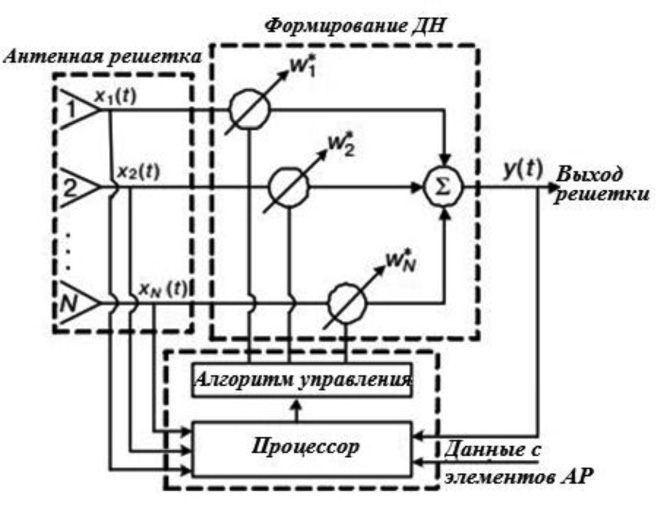
Рис. 1. Функциональная схема адаптивной антенной решетки из N элементов
Анализ данной схемы показывает, что в общем случае алгоритм функционирования представляет собой рекурсивную процедуру с положительной обратной связью [3], следовательно, данный процесс может быть описан уравнением [4]:
![]() , (1)
, (1)
где τ – постоянная времени контура адаптации; γ – коэффициент передачи в цепи обратной связи; I – единичная матрица; * – знак операции комплексного сопряжения; w – вектор весовых коэффициентов, соответствующий комплексным амплитудам возбуждения для каждого элемента антенны; S – вектор полезной части сигнала.
Ковариационная матрица помех R в случае действия J помеховых сигналов определяется выражением:
![]() , (2)
, (2)
где δ – мощность тепловых шумов в канале адаптивной антенной решетки; Vj – относительная мощность j-го помехового сигнала; ![]() – транспонированный вектор несущих колебаний помехового сигнала; Т – знак операции транспонирования.
– транспонированный вектор несущих колебаний помехового сигнала; Т – знак операции транспонирования.
Критерий оптимизации – величина отношения «сигнал/шум» – в рассматриваемом процессоре может быть вычислена с использованием выражения [4]:
![]() . (3)
. (3)
Анализ результатов моделирования
С использованием приведенных выше соотношений в языковой среде MathCad 15 была разработана программа, используемая для проведения исследований в модуле «Адаптивная антенная решетка». Программа включает несколько блоков: задание исходных данных; моделирование переходного процесса в контуре, включая получение окончательной диаграммы направленности и вычисление отношения «сигнал/шум»; исследование переходного процесса в контуре в различные моменты времени. Программа позволяет иллюстрировать в различные моменты переходного процесса изменение формы диаграммы направленности и величины отношения «сигнал/шум». На рис. 2 и 3 приведены примеры работы данного модуля для случая прихода одного полезного и одного помехового сигнала на линейную антенную решетку из 11 элементов, расположенных в излучающем раскрыве с шагом, равным половине длины волны. При этом на рис. 2 и в таблице приводятся результаты исследований влияния параметров помеховой обстановки на глубину формируемого «нуля» диаграммы направленности, обеспечивающего максимальное для данного случая значение критерия отношения сигнал/шум, а также непосредственно на величину критерия. При проведении исследований полагалось, что относительная мощность помех составляла 1000. Количество помех варьировалось от одной до двух, поскольку рассматривались самые простейшие из возможных случаи помеховой обстановки. Считалось, что две помехи могли приходить либо с одной стороны относительно главного лепестка диаграммы направленности (несимметричный случай), либо симметрично относительно главного лепестка диаграммы направленности. Для оценки получаемых значений используется потенциальное значение величины отношения «сигнал/шум», равное, как следует из теории [6], числу элементов антенной решетки.
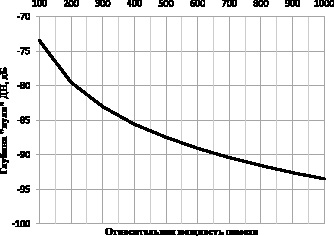
Рис. 2. Зависимость глубины формируемого «нуля» диаграммы направленности от мощности помехи
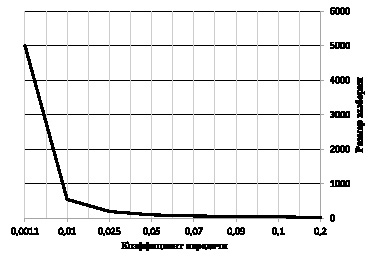
Рис. 3. Влияние коэффициента передачи на длительность переходного процесса
Зависимость величины отношения «сигнал/шум» от параметров помеховой обстановки
|
Помеховая ситуация |
Отношение «сигнал/шум», дБ |
|
Потенциальное значение в отсутствие помех |
11 |
|
Одна помеха |
10,16 |
|
Две помехи одинаковой мощности с разных сторон главного лепестка |
10,14 |
|
Две помехи одинаковой мощности с одной стороны главного лепестка |
9,95 |
Анализ получаемых при проведении исследований влияния параметров помеховой обстановки на характеристики адаптивной антенной решетки с помощью разработанного модуля позволяет сделать следующие выводы. Во-первых, при приходе двух помех с одной стороны главного лепестка деформирование главного лепестка больше, чем в случае прихода помех с разных сторон. Во-вторых, при приходе двух помех одинаковой мощности симметрично с разных сторон главный лепесток диаграммы направленности остается симметричным, что подтверждается известным патентом [5]. В-третьих, для обеспечения максимально достижимого значения отношения «сигнал/шум» при более мощных помехах требуется формирование «нулей» диаграммы направленности большей глубины: чем мощнее помеха, тем глубже должен быть «нуль» у формируемой диаграммы направленности. Наконец, в-четвертых, помехи, приходящие с одной стороны главного лепестка диаграммы направленности, снижают величину отношения сигнал/шум на 0,19 дБ по сравнению со случаем симметричного прихода и на 0,21 дБ по сравнению со случаем прихода одной помехи.
Рис. 3 иллюстрирует результаты исследований влияния параметров контура Хауэлса-Аппельбаума (значения коэффициента передачи в цепи с положительной обратной связью γ) на длительность переходного процесса, оцененную количеством накопленных выборок. Анализ данного рисунка позволяет обучаемому сделать вывод о том, что большие значения коэффициента передачи обеспечивают достижение требуемого значения критерия оптимальности при меньших размерах накопленных выборок. Так, при γ = 0,2 размер накопленных выборок должен составлять 25, а при коэффициенте обратной связи 0.0011 число накопленных выборок увеличивается до 104. Следовательно, длительность переходного процесса в первом случае будет в 400 раз меньше, чем во втором. Таким образом, чем больше коэффициент обратной связи, тем меньшее время требуется системе управления на обучение, тем более скоростной будет работа адаптивной антенной решетки.
Выводы
Выполнено обоснование использования информационных технологий при реализации компетенций по формированию поведенческой модели на примере разработки модуля «Адаптивные антенные решетки» в курсе дисциплины «Устройства СВЧ и антенны» направления обучения 11.03.01 Радиотехника. Показано, что актуальность разработки модуля обусловлена необходимостью обучения будущих радиотехников особенностям функционирования подвижных систем связи в условиях сложной, постоянно изменяющейся помеховой обстановки. Выполненный анализ функциональной схемы адаптивной антенной решетки позволил выделить основные параметры, исследование которых целесообразно осуществлять с использованием информационных технологий. В качестве данных параметров при разработке модуля были использованы: величина коэффициента передачи в цепи обратной связи вычислителя адаптивной антенной решетки; количество помеховых сигналов, их относительная мощность и направления прихода, т.е. параметры помеховой обстановки. Приведенный пример получаемых с использованием разработанной в языковой среде MathCad 15 результатов показывает, что обучающиеся по направлению подготовки 11.03.01 Радиотехника могут проводить исследования влияния параметров помеховой обстановки на характеристики адаптивной антенной решетки, а также влияния параметров контура адаптации на величину отношения «сигнал/шум», т.е. критерия, с помощью которого оценивается качество в канале связи. Получаемые при этом результаты являются за счет применения информационных технологий наглядными и позволяют легче усвоить известные положения теории адаптивных антенных решеток.



