До настоящего времени технический ресурс и гарантийный срок работы СВТ определялись разработчиком-изготовителем на стадии постановки СВТ на производство расчетным путем, а наработка на отказ подтверждалась специальными испытаниями определенной выборки СВТ на надежность (наработку на отказ и/или долговечность).
Однако используемые методы, испытательные приборы и стенды, в т.ч. ускоренные и форсированные, не могут обеспечить всего многообразия фактических эксплуатационных условий, в которые «попадают» СВТ на объектах автоматизации, в связи чем, все имеющиеся «паспортные параметры» являются приближенными. Поэтому на объектах и в технологических процессах повышенной опасности применяется резервирование (дублирование, троирование и т.д.) и профилактические «остановы» для ремонта или замены блоков и устройств, чтобы избежать аварий, взрывов и пожаров, из-за «внезапного» отказа СВТ.
В то же время и резервирование (холодное и горячее), и периоды восстановительных ремонтов, и ремкомплекты для них выполняются только расчётным путем, а их достоверность «оценивается косвенно» (по статистике отказов). При этом крайне редко, как правило, при катастрофических авариях (Чернобыль, Саяно-Шушенская ГЭС и т.д.), когда проводятся многочисленные экспертизы с отказавшими или с поврежденными объектами, удается определить причины отказов и сравнить их с расчетными показателями надежности и безопасности.
Поэтому для получения более достоверной информации о надежности и пожаробезопасном ресурсе электроприборов, в т.ч. и СВТ, был разработан вероятностно-физический метод (ВФМ) стендовых испытаний электроприборов [1–3] и предложены модули термоэлектронной защиты (МТЭЗ), позволяющие, во-первых, достоверно определить их технический ресурс при ускоренном технологическом прогоне, во-вторых, обнаруживать пожароопасный отказ и отключать электроприбор до загорания в нём электрорадиоматериалов, а в третьих, и это главное, определить его пожаробезопасный ресурс, который при этом становится соизмеримым с его техническим ресурсом [7].
Однако распространения предложенный метод не получил, наверное из-за «нетехнологичности и хрупкости» позисторных термозондов» [4], а также сложности автоматизированного стендового оборудования [5], с уникальными для того времени вычислительными ресурсами (УВК СМ-1210 с векторным режимом ПС 3000 под операционной системой Юникс и модернизированным ПВВ под модули УСО ТВСО).
В настоящее время вычислительные ресурсы СВТ автоматизированных систем, в частности, на объектах повышенной опасности (АЭС, НПЗ, терминалы ГСМ и т.д.), давно превзошли необходимые для указанного метода и быстродействие, и объем оперативной памяти, и возможности программного обеспечения, а вместо позисторных термозондов и прецизионных шунтов можно использовать микросхемы, измеряющие температуру и потребляемую электроэнергию [12, 13].
Следовательно, введение в каждое устройство СВТ «микросхемного модуля термоэлектрозондирования», данные с которого процессор, контроллер или микропроцессор устройства СВТ может передать на верхний уровень АСУ (АСУТП, АСК, АСУП и т.д.), является необходимым и достаточным условием реализации метода.
Разработанный метод определяет «текущие» интенсивности и вероятности отказов элементов изделий по модифицированному уравнению Аррениуса-Эйринга [1–3]:
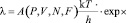
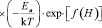, (1)
где l – текущая интенсивность отказа элемента, 1/час; А = ki∙λО – произведение безразмерных коэффициентов, зависящих от давления, влажности, вибраций и т.д.) на интенсивность отказов при хранении (λО), 1/час; k – постоянная Больцмана, 1,38·10-23 Дж/К; Т – температура элемента, °К; h – постоянная Планка, 6,626× ×10-34 Дж·с; Ea – эффективная энергия активации отказа, Дж; f(H) – функция нетермической (энергетической) нагрузки.
Уравнение (1) имеет решение, если определены температуры внутреннего объема изделия [T(t)] и окружающего воздуха [TВОЗД.(t)], а также измерены потребляемые изделием энергии [E(t)] при известных минимальных (λmin), номинальных (λном) и максимальных (λмах) значениях интенсивности отказов всех элементов. Указанные переменные определялись с помощью позисторных термозондов и электрозондов блоков и плат ([Wp(t)]. Тогда решением системы уравнений (2) теплового баланса и Навье-Стокса (прямая и обратная задачи тепловой локации), определялись все текущие коэффициенты энергетических нагрузок элементов [EL(t)]:
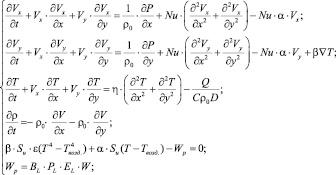(2)
f(H) ≈ ЕL = (β·S·σ(T4–T4ВОЗД) + α·S(T–TВОЗД))/(WL·BL·PL),
где α, β, ρ, η – коэффициенты, Nu – число Нуссельта; С – теплоемкость, D – расстояние, σ – постоянная Стефана-Больцмана, Sи – площадь поверхности источника тепла (ЭРЭ), WP – потребляемая источником тепла мощность (фактическая), ТВОЗД. – температура окружающего источника тепла воздуха/зонда, Т – искомая/измеренная температура источника тепла (ЭРЭ, платы, стенки и т.д.), BL – коэффициент энергетической нагрузки конструктива (блока, изделия), PL – коэффициент энергетической нагрузки платы (модуля), W – номинальная (паспортная) потребляемая мощность, ЕL – коэффициент энергетической нагрузки ЭРЭ (микросхемы, резистора и т.п.).
Знание функций энергетической нагрузки ЭРЭ – f(H) – превращает λ в функцию, у которой для любого ЭРЭ известны минимальное (λО), номинальное (λном), максимальное (λмах) значения интенсивности отказов, а также интенсивность отказов при хранении (λхр), что позволяет построить и аппроксимировать «семейство» λ-кривых в границах λхр(Т) и λмах(Т), а также логарифмированием получить функцию эффективной энергии активации отказов каждого ЭРЭ – Еai (Н,Т).
Таким образом, подставляя в уравнения Аррениуса-Эйринга текущие значения функций энергетических нагрузок каждого ЭРЭ, текущие значения температур их корпусов, текущие значения функций эффективной энергии активации отказа, им соответствующие, а также текущие значения параметров окружающей среды (температуры, давления и т.д.), получаем текущие интенсивности отказов ЭРЭ, т.е. функции λ (Н,Т,Р), которые описываются γ-распределениями [1–3].
При этом предварительное нахождение параметров γ-распределения случайной величины λi в данном случае сводилось к задаче определения параметров В и С функции γ-распределения по заданным двусторонним доверительным интервалам (λн < λ< λмах):
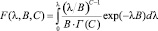
при В > 0, С > 0,5,Г(С)-гамма-функция, (3)
т.е. по заданным ее квантилям λн = λmin и λв = λмах уровня доверительной вероятности (р = 0,95) соответственно L и 1-L, где L = (1-р)/2, к решению системы уравнений:
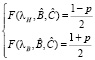(4)
с последующей заменой переменной х = 2λ/В, переводящей γ-распределение в обобщенное χ2 – распределение (для снятия ограничений относительно целочислености v), после чего делением одного уравнения на другое находится
q (v) = λв / λн. (5)
Полученные значения q (v) = χ2 1-L(v)/ χ2L(v) являются монотонной функцией от v, имеющей при λв/λн > О единственный корень, а по вычисленному v (а следовательно, и С = v/2) находится и второй параметр γ-распределения:
В = 2λн/χ2L(v) = 2 λв/χ2 1-L(v). (6)
С помощью термозондирования тепловых потоков от ЭРЭ позисторными датчиками [4] и определения потребляемой электроэнергии с помощью прецизионных шунтов [5] удалось устранить ограничения, возникающие при решении указанного уравнения (1) в двумерном приближении Обербека-Бусcинеска в «прямой и обратной задачах» тепловой локации элементов, чтобы получить значения функции нетермической нагрузки f(H) [1, 3].
Дальнейшее вычисление прогнозируемого технического ресурса на плату, блок или устройство, в связи с аддитивностью текущих интенсивностей отказов, осуществляется интегрированием по времени их суммарного значения.
Понятие «пожаробезопасный ресурс» было введено одновременно с указанным выше методом [1–3], однако до сих пор не «прижилось». Положение усугубилось в 2008 году, когда 123-ФЗ был введен в действие «Технический регламент о требованиях пожарной безопасности», в котором были введены «пожарные риски», научной теории которых нет до сих пор.
Конечно, отечественный ГОСТ 12.1.004 «Пожарная безопасность. Общие требования», построенный на теории вероятностей, имеет существенные недостатки, которые «появились при его рождении» в 1974 году и были обусловлены, во-первых, отсутствием «связки» методов экспериментальных исследований пожарной опасности веществ и материалов (по ГОСТ 12.1.044) с электроприборами, технологическими процессами и объектами техносферы, где они применяются, во-вторых, ошибочной методологией «внесения неисправностей» в оборудование, нарушающей принцип независимости событий в них, а в-третьих, некорректным применением понятий теории вероятностей, проявившейся в нарушениях размерности событий [9–11].
В связи с тем, что введенные 123-ФЗ «пожарные риски» повторили и «усугубили» ошибки ГОСТ 12.1.004, покажем необходимость и возможность их устранения, а также докажем достаточность теории вероятностей для корректного применения её в методиках, предназначенных для оценки пожарной опасности любого объекта, в т.ч. при формировании декларации о пожарной безопасности, без введения дополнительных и «размытых» понятий «пожарных рисков».
Вероятность события является безразмерной величиной, а ГОСТ 12.1.004, как и «Технический регламент», фиксирует допустимый уровень вероятности пожара в оборудовании или объекте, в т.ч. «пожарного риска» – 10-6 в год, что, с точки зрения теории надежности и теории вероятностей, является интенсивностью событий – λ с общепринятой размерностью 1/час, т.е. 1,14∙10-10 час-1, т.к. приходится одну миллионную разделить на 8760 часов, из которых состоит год [1, 6].
Эта ошибка может быть устранена, путем введения понятия «пожаробезопасный ресурс» (материала, изделия и т.д.) и требования его соизмеримости с техническим ресурсом, т.е. со сроком эксплуатации материала, оборудования, помещения и объекта. Тогда корректная формулировка прозвучит так: вероятность пожара в оборудовании и/или объекте не должна превышать 10-6 в течение всего срока их эксплуатации.
В случае общепринятого в теории надежности (и в ГОСТ 12.1.004) экспоненциального распределения логарифмированием функции распределения при известном времени «пожаробезопасного ресурса» (tПБР) корректно определяется допустимая интенсивность λД пожароопасного отказа материала, оборудования, помещения и объекта при «вводе в эксплуатацию» [6, 8]:
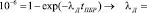
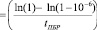. (7)
Если же возникло желание ввести понятие «пожарный риск», чтобы, например, уйти от «неблагозвучности понятия интенсивности возникновения пожара», то в рамках теории вероятности существует функция риска – h(х), которая определена, как отношение функции плотности вероятности – f(x), к функции выживания – S(x) в точке х, и в нашем случае (экспоненциального распределения) она равна именно λД [14]:
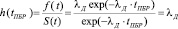. (8)
Необходимо исключить методологию внесения неисправностей при испытаниях на пожарную опасность радиоэлектронного и электротехнического оборудования и приборов, в связи с тем, что она требует применения сложного раздела теории надежности – теории зависимых отказов, т.к. искусственное «выключение», т.е. замыкание или обрыв какого-либо элемента изделия вызывает аварийный режим не в нем, а в схемотехнически связанном другом элементе. Поэтому дальнейший расчет вероятности пожара является некорректным, т.к. при этом нарушаются условия применимости формул распределения вероятностей, требующих независимости событий [6, 9].
Эта ошибка устраняется, путем применения вероятностно-физической методологии – модели дополнительного тепловыделения каждого элемента при пожароопасном отказе, полученная в виде логнормальных функций распределения [1, 2]:
FЭ(Q) = 1 – vЭ ∙ [1 – GЭ(z)], (9)
где FЭ(Q) – вероятность дополнительного тепловыделения, vЭ – доля пожароопасных отказов (короткое замыкание, пробой, обрыв), GЭ(z) – условная функция распределения (при возникновении пожароопасного отказа ЭРЭ) случайной величины z = lg Q, Q = k∙U∙I∙t – Джоулево тепло пожароопасного отказа ЭРЭ.
Дополнительное тепловыделение пожароопасного отказа, нагревая материал отказавшего ЭРЭ, воспламеняет его при переходе процессов деструкции и пиролиза в самоускоряющуюся фазу по критерию Семёнова или «зажигает соседа» по критерию Зельдовича, если собственная температура воспламенения выше «соседней», а плотность теплового потока равна критической. Тогда, решая систему (10) неравенств Семёнова, Зельдовича и Франк-Каменецкого в точке воспламенения (Твс), т.е. при Se = 0,368, Fк = 2,00 и Ze = Q/S, определяются: Еа – энергия активации воспламенения образца (11), K – предэкспонент (6) и Н – тепловой эффект реакции в газовой фазе (12), после чего вычисляются энергии и теплоты – ЕDi и НDi стадий деструкции по формулам (11, 12), при температурах (Тр, Тпл, Ттл) этих стадий [6]:
(10)
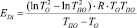; (11)
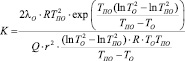; (12)
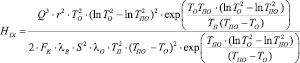; (13)
где Ze – критерий Зельдовича; l – коэф. теплопроводности газовой фазы; R – газовая постоянная; Тп – температура печи; Еа – энергия активации деструкции образца; Н – тепловой эффект реакции в газовой фазе; K – предэкспонент; Se – критерий Семенова; Q – теплота, подведенная к образцу; V – объём образца; S – площадь поверхности образца; a – коэф. теплоотдачи образца; Тпо – температура поверхности образца; Fк – критерий Франк-Каменецкого; r – линейный размер образца; λо – коэф. теплопроводности образца; То – температура образца.
Приведенная выше математическая модель, позволяет определить интенсивности пожароопасных отказов элементов (λПО = λН,Т∙vЭ) и интенсивности их воспламенений (λВ = λПО∙FЭ), зафиксировав критические теплоты каждого элемента – Qэ, после чего интегрированием вычисляет вероятности их воспламенений (Fв).
Расчеты по системе неравенств (10) и модели дополнительного тепловыделения (9) проводятся для каждого элемента пожарной нагрузки объекта и его «соседей». Для этого необходима их топология, т.е. геоинформационная среда, а для вероятностной оценки «превращения воспламенения в пожар», вводится функция (14) «маятник события» [9], формирующая из топологии элементов пожарной нагрузки на объекте (в частности, из матрицы вероятностей воспламенений) «матрицу распространения огня» (Fр), позволяющую вычислить вероятность пожара каждого элемента (Fп = Fв∙Fр):
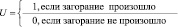. (14)
Таким образом, устраняется методологическая и логическая незавершенность оценки пожарной опасности любого изделия или объекта (ГОСТ 12.1.004 в своих вероятностных параметрах и формулах практически не использует ни одного из 20 значений номенклатуры показателей пожаровзрывоопасности веществ и материалов, приведенных в ГОСТ 12.1.044), путем использования методов термического анализа для определения (по критериям Семенова, Франк-Каменецкого и Зельдовича) существующих и дополнительных параметров пожаровзрывоопасности веществ и материалов, из которых изготовлены изделия и объекты, а с помощью вероятностно-физических уравнений, описывающих тепловыделение пожароопасного отказа, корректно связывает их с вероятностью пожара [1, 6].