Вопросам полноты системы корневых векторов несамосопряженных операторов посвящена большая серия работ как советских, так и зарубежных математиков, появившихся в основном после 50-х годов прошлого века. А первые результаты по вопросам полноты корневых подпространств несамосопряженных операторов, по-видимому, были получены Б. Биркгофом в начале прошлого столетия. Впоследствии существенные результаты в этом направлении были получены Я. Тамаркиным в случае обыкновенных несамосопряженных дифференциальных операторов с регулярными краевыми условиями. Эти авторы отправлялись от методов Коши и Пуанкаре, основанных на изучении асимптотических свойств резольвенты. Что касается краевых задач для дифференциальных уравнений в частных производных, то ввиду сложного строения резольвенты, в течение продолжительного времени не удавалось получить ничего аналогичного. Лишь в 30-х годах Т. Карлеману оригинальным образом удалось установить полноту системы корневых векторов для эллиптических операторов второго порядка. Однако вопрос о полноте системы корневых векторов в случае дифференциальных операторов с частными производными оставался и после работ Карлемана еще продолжительное время открытым.
Положение это изменилось лишь в 1951 г. в связи с появлением работы М.В. Келдыша [2], в которой получены теоремы о полноте системы корневых векторов и теоремы об асимптотических свойствах собственных чисел для широкого класса полиноминальных пучков несамосопряженных операторов. Эти теоремы позволили получить важные результаты в краевых задачах для дифференциальных уравнений в частных производных, они привели также к новым сильным результатам и в случае обыкновенных дифференциальных уравнений.
Вышеупомянутая работа М.В. Келдыша стимулировала появление глубоких исследований по вопросам полноты системы корневых векторов несамосопряженных операторов. Библиография этих работ весьма многочисленна (можно посмотреть, например в [1]).
Мы будем рассматривать линейные несамосопряженные операторы A, действующие в гильбертовом пространстве H и обладающие дискретным спектром. Последнее означает что все точки спектра оператора A (за исключением, быть может, одной) являются изолированными и соответствующее им подпространство конечномерно. Конечномерное инвариантное подпространство оператора A, относящееся к некоторой точке λ, принято называть корневым подпространством.
Корневое подпространство может быть охарактеризовано как совокупность элементов f, удовлетворяющих при некотором целом n ≥ 1 уравнению
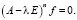
Дискретным сектором, как известно, обладают вполне непрерывные операторы, а также неограниченные (например, дифференциальные) операторы, имеющие вполне непрерывные обратные.
Основной задачей нашей работы является исследование условий, при которых система корневых подпространств оператора A полной в гильбертовым пространстве H или области значения этого оператора. Поясним, что систему корневых подпространств некоторого оператора принято называть полной в гильбертовом пространстве H, если любой элемент f∈H можно с наперед заданной точностью приблизить по норме конечной линейной комбинацией элементов, каждый из которых принадлежит одному из корневых подпространств. Хорошо известно, что если некоторый вполне непрерывный оператор является самосопряженным, то система его конечномерных корневых подпространств полна в области значений оператора (при этом корневые подпространства оказываются собственными).
В случае общего вполне непрерывного оператора полнота может и не иметь места. Простейшим примером такого рода служит оператор интегрирования
,
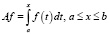который действует в гильбертовом пространстве функций, обладающих интегрируемым по Лебегу квадратом на интервале (a, b). Это пространство мы будем в дальнейшем обозначать через L2(a, b). Этот оператор, во-первых, вполне непрерывный; во-вторых, он обладает лишь единственной точкой спектра и не имеет ни одного собственного вектора. Следовательно, корневое подпространство у него вообще отсутствует.
Более того, существуют вполне непрерывные операторы, которые вообще не имеют собственных значений (конечнократных). Поэтому в несамосопряженном случае вопрос полноты приобретает особый интерес.
В ряде работ М. Отелбаева [4, 5, 6, 7, 8] найдены двусторонние оценки собственных чисел самосопряженных операторов типа Шредингера. Такие результаты имеют ряд преимуществ перед известными классическими формулами распределения собственных чисел: во-первых, для классических формул нужен ряд условий; во-вторых, они не всегда справедливы [9]; в-третьих, не позволяют судить о малых собственных числах. Результаты такого характера впервые появились в работах [6, 7].
Цель работы состоит в получении условия полноты собственных и присоединенных элементов несамосопряженного оператора Шредингера высокого порядка, заданных во всем пространстве.
Работа носит теоретический характер. Результаты работы могут найти применение в различных вопросах спектральной теории дифференциальных операторов и теории рядов, а также в задачах квантовой механики, приводящих к изучению сингулярных несамосопряженных дифференциальных операторов.
Основные результаты сформулированы в терминах некоторых вспомогательных функций, которые достаточно эффективно строятся из коэффициентов уравнения. Впервые такие функции были введены в работах М. Отелбаева [5, 6].
Пусть L – замыкание в L2(Rn) дифференциального оператора L0, определенного на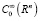 
равенством
,
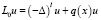где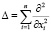 
– оператор Лапласа, l – положительное целое число, q(x) – ограниченная в каждом компакте комплекснозначная функция, такая, что
. 
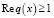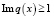. (1)
Введем некоторые необходимые обозначения и определения.
(2, l) – емкость замкнутого множества F относительно открытого множества W⊂Rn, содержащего F, называется число
,
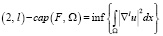где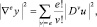 
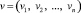
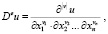
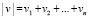
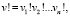а infimum берется по всем 
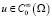, равным единице в окрестности F.
Через Qd(x) будем обозначать куб с центром в точке x, с ребрами d, параллельными координатным осям, а через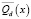 
– его замыкание, если положение центра куба не важно, вместе Qd(x) и 
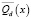будем писать Qd и 
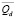соответственно. Совокупность всех компактных подмножеств F куба 
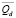, удовлетворяющих неравенству
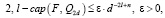
обозначим через N2, l, ε(Qd). При 2l > n и достаточно малом ε множество N2, l, ε(Qd) пусто.
Теперь ограниченной в каждом компакте комплекснозначной функции q(x) сопоставим функцию
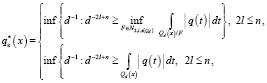(2)
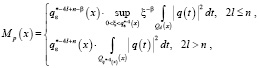(3)
, 
.
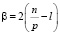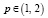Основная теорема. Пусть 2l > n и выполнены следующие условия:
1) 
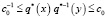при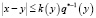 
, где k(y) ≥ δ > 0 – непрерывная функция, стремящаяся к + ∞ при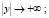 
2) 
;
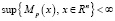3) оператор L–1 вполне непрерывен.
Предположим, что
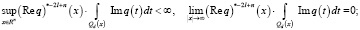
и при некотором θ∈(0, + ∞)
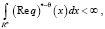
тогда система корневых векторов оператора L полна в L2(Rn).
Для доказательства этой теоремы в дальнейшем нам потребуются следующие леммы.
Лемма 1. Если x∈Rn, то
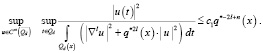
Для доказательства этой леммы нужно воспользоваться преобразованием подобия. Тогда она сводится к случаю d = 1. В этом случае лемма вытекает из известной леммы о продолжении [8] и из непрерывности вложения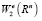 
в пространстве непрерывных функций.
Лемма 2. Пусть r(x) – локально интегрируемая в Rn функция. Тогда
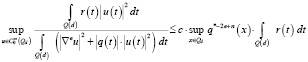. (4)
Доказательство. Пусть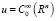 
. Покроем Rn семейством кубов 
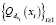в соответствии с леммой Безиковича-Гуцмана [10]. Тогда
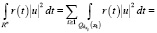
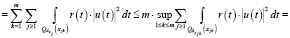
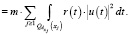
Здесь через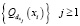 
обозначено подсемейство на, котором достигается указанный supremum.
Далее, пользуясь леммой 2 и известной неравенств (см. [8], лемму 4.3) получаем:
,
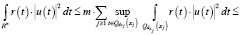
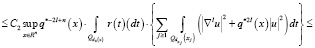
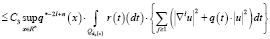поскольку кубы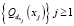 
по построению не пересекаются. Поэтому
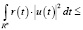
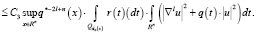
Отсюда получаем (4). Лемма 2 доказана.
Лемма 3. Пусть r(x) локально суммируемая, неотрицательная в Rn функция. Тогда множество
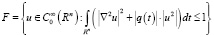
относительно компактно по норме
,
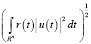если
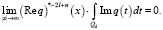
Доказательство. Как известно, если W – некоторый компакт в Rn достаточно гладкий границей, то множество F относительно компактно в метрике
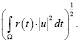
Покроем Rn/F кубами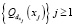 
, центры которых принадлежат этому множеству. Далее, рассуждая, как в лемме 3, получаем
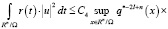
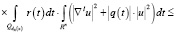
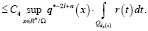
Здесь мы воспользовались принадлежностью и к F. Из условия леммы вытекает, что при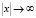 
оцениваемый интеграл стремится к нулю, т.е. для любого ε > 0 можно указать такое компактное множество Wε, что
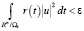
Лемма 3 доказана.
Доказательство основной теоремы. Пусть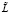 
– оператор, аналогичный L, соответствующий потенциалу Req(x). В силу условия (1) имеем, что 
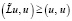. С другой стороны, из условия основной теоремы оператор 
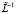имеет конечный тип. Из леммы 3 и условия доказываемой теоремы получаем, что оператор 
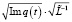вполне непрерывен. Но тогда вполне непрерывен и оператор 
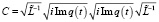, и по теореме М.В. Кельдыша [2] система корневых векторов операторного уравнения
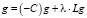
полна в L2(Rn). Легко заметить, что система корневых векторов последнего операторного уравнения совпадает с системой корневых векторов оператора L(E + C) или обратного к нему оператора (E + C)–1 L–1.
Теорема доказана.
Доказательство следующей теоремы вытекает из общей теоремы Келдыша-Лидского [9].
Теорема 1. Пусть 4l > n и выполнены условия основной теоремы. Тогда, если
,
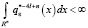то система корневых векторов оператора L2 полна в L2(Rn).