В [3] было показано, что описание движения сплошной среды в инерциальной системе отсчета (ИСО) и переход к неинерциальной (НСО) требует в общем случае выхода за рамки плоского пространства-времени. Это связано с заданием не только силового поля, действующего на частицы среды, но также и наложения условий на кинематические характеристики континуума с помощью уравнений структуры [3–7]. Эти уравнения связывают тензор Римана – Кристоффеля с тензорами скоростей деформаций, угловой скорости вращения и векторами первой кривизны мировых линий частиц среды. В результате система уравнений оказывается переопределенной и не реализуема в пространстве Минковского. Эта система разрешима при рассмотрении движения среды в римановом пространстве или в более общем случае в пространстве метрической связности. Если не накладывать на характеристики континуума дополнительных условий, а ограничиться лишь интегрированием уравнений движения, например, в плоском пространстве-времени, то никакого выхода за рамки плоского пространства-времени при стандартном переходе из ИСО к НСО не происходит. Однако если при переходе к сопутствующей среде системе в уравнениях движения для лагранжевых частиц с номерами 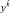 для вычисления расстояния между соседними частицами брать не проекцию полного дифференциала
для вычисления расстояния между соседними частицами брать не проекцию полного дифференциала 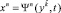 , от эйлеровых координат xn на гиперплоскость одновременности, а дифференциал при фиксированном времени t, как это делается в классической механике [8], то получаем элемент квадрата интервала в синхронной системе в общей теории относительности (ОТО). Пространственное сечение при таком подходе будет плоским.
, от эйлеровых координат xn на гиперплоскость одновременности, а дифференциал при фиксированном времени t, как это делается в классической механике [8], то получаем элемент квадрата интервала в синхронной системе в общей теории относительности (ОТО). Пространственное сечение при таком подходе будет плоским.
Анализ уравнений Эйлера и относительного тензора кривизны
Исследуем в ньютоновском приближении метрику пространства-времени для наблюдателей, движущихся вместе со средой. В этом приближении метрика сводится к виду
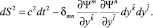 (1)
(1)
В метрике (1) в качестве эйлеровых координат ИСО выбраны декартовы координаты, в которых gmn = –δmn, t – ньютоново абсолютное время. Следует отметить, что метрика (1) в общем случае риманова с плоским пространственным сечением. Этот результат на первый взгляд является неправдоподобным, однако метрика (1) допускает простое геометрическое и физическое толкование.
В качестве примера рассмотрим нежесткий стержень, элементы которого движутся вдоль оси стержня с разными скоростями. Вблизи стержня параллельно ему движется частица со скоростью, превосходящей скорости частиц стержня. Условимся, что наблюдатели на стержне в качестве времени используют часы ИСО пространства Минковского. Пусть показания часов, когда частица поравнялась с задним концом стержня, t1, а в момент обгона часы показывали t2. Время, затраченное на обгон, равно (t2 – t1). Ясно, что относительную длину мировой линии частицы, при обгоне стержня, можно вычислить по теореме Пифагора. Относительная длина мировой линии частицы, когда стержень имеет бесконечно малые размеры, дается формулой (1). Элемент интервала (1) получается из псевдоевклидова интервала с помощью закона движения 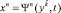 , а дифференциал от xn вычисляется при фиксированном значении t, т.е. не является полным. Поэтому квадрат элемента интервала, получаемого вычитанием из квадрата временного элемента квадрата пространственного элемента, заданного в лагранжевой сопутствующей НСО, в общем случае приводит к неевклидову пространству-времени с плоским пространственным сечением.
, а дифференциал от xn вычисляется при фиксированном значении t, т.е. не является полным. Поэтому квадрат элемента интервала, получаемого вычитанием из квадрата временного элемента квадрата пространственного элемента, заданного в лагранжевой сопутствующей НСО, в общем случае приводит к неевклидову пространству-времени с плоским пространственным сечением.
Обычно при переходе из ИСО в НСО рассматривают элемент абсолютной длины мировой линии частицы. Элемент интервала получается из псевдоевклидова интервала с помощью закона движения 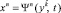 , а дифференциал от xn является полным. Поэтому квадрат элемента (в отличие от (1)) содержит члены, зависящие от абсолютной скорости частицы, изменяется g00 компонента и появляются отличные от нуля g0k компоненты метрического тензора. Однако пространство-время при этом остается плоским. Очевидно, что абсолютная длина мировой линии рассматриваемой частицы не равна относительной длине мировой линии этой частицы.
, а дифференциал от xn является полным. Поэтому квадрат элемента (в отличие от (1)) содержит члены, зависящие от абсолютной скорости частицы, изменяется g00 компонента и появляются отличные от нуля g0k компоненты метрического тензора. Однако пространство-время при этом остается плоским. Очевидно, что абсолютная длина мировой линии рассматриваемой частицы не равна относительной длине мировой линии этой частицы.
Пространственная метрика в лагранжевой сопутствующей НСО в согласии с (1) имеет вид
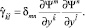 (2)
(2)
Как известно из механики сплошной среды [8]
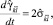 (3)
(3)
где 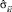 – тензор скоростей деформаций в сопутствующей СО. Так как лагранжевы
– тензор скоростей деформаций в сопутствующей СО. Так как лагранжевы 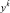 при движении каждой частицы остаются неизменными, то
при движении каждой частицы остаются неизменными, то 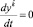 , и поэтому
, и поэтому
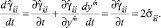 (4)
(4)
Рассмотрим движение разряженного газа в ньютоновском поле тяжести, используя уравнение движения в форме Эйлера и уравнение неразрывности.
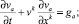
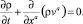 (5)
(5)
Дифференцируя уравнение (5) по xb, имеем
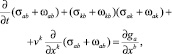 (6)
(6)
или
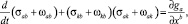 (7)
(7)
где
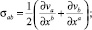
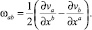 (8)
(8)
В (8) σab, ωab – тензоры деформаций и угловой скорости вращения в нерелятивистской механике в переменных Эйлера. Рассмотрим случай, когда среда движется без вращений
ωab = 0.
Свертывая (6) по a, b, получим в переменных Лагранжа
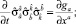 (9)
(9)
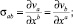
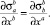
Последнее соотношение в лагранжевых переменных сводится к виду
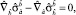 (10)
(10)
где ковариантные производные вычисляются по метрике (2). Для вычисления тензора Риччи воспользуемся метрикой (1) и результатом [2] для синхронной системы отсчета с плоской пространственной метрикой.
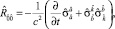 (11)
(11)
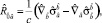 (12)
(12)
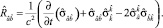 (13)
(13)
Можно показать, что при отсутствии вращений справедливо равенство
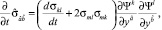 (14)
(14)
используя которое, имеем для выражения (13) соотношение
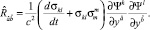 (15)
(15)
Учитывая (7), находим при отсутствии вращений
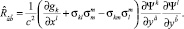 (16)
(16)
Среда, движущаяся в собственном поле тяжести, имеет 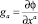 , где ϕ – потенциал поля тяжести, удовлетворяющий уравнению Пуассона. Из соотношений (9), уравнения Пуассона находим для (11)
, где ϕ – потенциал поля тяжести, удовлетворяющий уравнению Пуассона. Из соотношений (9), уравнения Пуассона находим для (11)
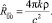 (17)
(17)
Соотношение (12) с учетом (10) дает
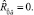 (18)
(18)
Выражение (16) в совокупности с уравнением Пуассона представим в удобной для дальнейших исследований форме
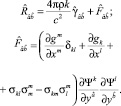 (19)
(19)
Соотношения (17)–(19) при условии, что в последнем выражении 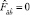 , представляют собой уравнения Эйнштейна, записанные в синхронной системе отсчета для пылевидной материи [2]. Очевидно, что в общем случае
, представляют собой уравнения Эйнштейна, записанные в синхронной системе отсчета для пылевидной материи [2]. Очевидно, что в общем случае 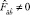 , так как в одном и том же силовом поле конгруенции мировых линий частиц среды обладают большим произволом.
, так как в одном и том же силовом поле конгруенции мировых линий частиц среды обладают большим произволом.
Эквивалентность ОТО с теорией Ньютона
Выясним, при каких частных условиях геометрия НСО, определяемая законами ньютоновой механики, и геометрия синхронной системы отсчета для пылевидной материи, определяемая уравнениями Эйнштейна, совпадают. Из вида метрики (2) следует, что искомые решения уравнения Эйнштейна справедливы в случае плоских пространственных сечений. А совпадение решений уравнений Эйнштейна с решениями ньютоновской механики возможно, если на конгруенции мировых линий частиц базиса наложить ограничение
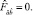 (20)
(20)
Исследуем сферически-симметричные движения сплошной среды, поле скоростей которых в переменных Эйлера в декартовых координатах есть
va = v(r, t)na; 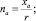 nana = 1. (21)
nana = 1. (21)
Используя уравнения Эйлера (5), условия симметрии (21), получим для системы (20) выражение
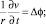
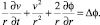 (22)
(22)
Рассмотрим некоторые частные случаи решения этой системы:
1. Для радиального движения разряженной среды в ньютоновском центрально- симметричном поле тяжести, создаваемом массивным телом, центр масс которого расположен в начале координат, имеем
Δϕ = 0; 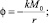
 (23)
(23)
где M0 – масса тела, создающего поле; v0 – значение скорости при r = r0. Из совместности выражений (22) и (23) получим
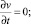
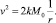 (24)
(24)
Решение (24) есть частный случай (23) при условии, что среда на бесконечности покоится. Интегрируя (24), получаем
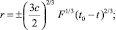
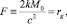 (25)
(25)
где rg – гравитационный радиус. Отметим, что в последнем соотношении скорость света c введена искусственно для удобства сравнения с другими результатами, и в результате в этой формуле она сокращается, как и должно быть при интегрировании уравнений движения в нерелятивистской механике. Выбор знака зависит от характера движения частиц. При движении по радиусу к центру выбирается знак «плюс», и знак «минус» – при расширении от центра. Постоянная t0 выбирается из требования, что при t = 0 должно быть r = r0, где r0 – лагранжева координата. Очевидно, что при падении частиц на центр текущий радиус лагранжевой частицы r(r0, t) уменьшается поэтому t < t0.
Метрика (1) в сферической системе координат имеет вид
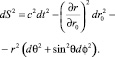 (26)
(26)
Используя закон движения (25), полагая
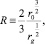 (27)
(27)
имеем для элемента интервала выражение
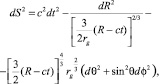 (28)
(28)
которое в точности совпадает с известной метрикой Леметра в ОТО [2]. Для нашего случая элемент интервала метрики Леметра означает квадрат относительной длины мировой линии пробной частицы, движущейся относительно свободно падающих по радиусу к центру невзаимодействующих друг с другом частиц в ньютоновском центрально-симметричном поле тяжести. При этом падающие частицы, имеющие на бесконечности нулевую скорость, образуют базис НСО. Характер сил, действующих на пробную частицу, не имеет значения.
Хотя метрика (28) и тождественна с соответствующей метрикой из ОТО, однако в нашем случае координаты и время, определяющие метрику, имеют ясный метрический смысл, чего в принципе не может быть в ОТО. Например, время падения T частицы базиса от начального значения радиуса r1 до текущего значения r(r1, T) является конечной величиной и определяется формулой
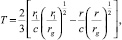 (29)
(29)
которая соответствует формуле из ОТО, когда в качестве времени используется собственное время частицы [1]. В нашем случае роль собственного времени играет ньютоновское время t.
2. Следуя работам [1, 2], рассмотрим ньютоновскую однородную изотропную космологическую модель, для которой имеем
v(r, t) = H(t)r. (30)
Систему (22), учтя уравнения Эйлера, запишем в виде
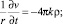
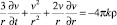 . (31)
. (31)
Из уравнений (30), (31) находим
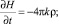
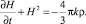 (32)
(32)
Откуда
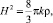 (33)
(33)
что соответствует случаю расширения при плотности равной критической. Так как закон эволюции Вселенной в ньютоновском приближении выведен в [1] для произвольной плотности, то воспользуясь результатами [1] для нашего случая, находим закон расширения
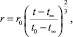 (34)
(34)
где (t0 – t∞) – «возраст» однородной модели Вселенной. Подстановка (34) в (26) приводит к выражению для квадрата интервала
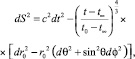 (35)
(35)
которое соответствует модели с плоским (евклидовым) пространством ОТО.
Заключение
Самым странным результатом, полученным в этой работе, является то, что точные решения уравнений Эйнштейна содержатся в качестве частных случаев нерелятивистской механики Ньютона, а не наоборот, как принято считать. Более подробные исследования релятивистской сплошной среды приведены в работах [9-12].



