Конечноэлементная схема позволяет задачу с бесконечным числом неизвестных привести к задаче с конечным числом неизвестных, решение которой принципиально возможно на вычислительных машинах.
С помощью конечноэлементной схемы получаем приближенное решение дифференциальной задачи, то есть задачи с начальными и граничными условиями.
Для выполнения условий устойчивости конечноэлементную схему нужно представить в виде некоторого линейного оператора в разные моменты времени. Условие устойчивости требует, чтобы собственные числа этого оператора не превосходили по модулю единицу в разные моменты времени. Если это условие не выполнено, тогда погрешности конечноэлементной схемы быстро возрастают и результат становится неприемлемым. Если это условие выполнено, тогда результат конечноэлементной схемы сходится к решению нестационарной волновой теории упругости.
Для оценки устойчивости конечноэлементной схемы применяется условие Куранта. Согласно условию Куранта скорость распространения возмущений в конечноэлементной схеме не должна быть меньше, чем в исходной дифференциальной задаче. Если это условие не выполнено, то результат конечноэлементной схемы не стремится к решению исходного дифференциального уравнения. Другими словами, за один шаг по времени возмущение не должно пробегать более одного конечного элемента.
Свойство устойчивости явной конечноэлементной схемы в основном зависит от величины шага по времени при сравнении с временами изучаемых физических нестационарных волновых процессов.
Некоторая информация о применяемом численном методе, алгоритме и комплексе программ приведена в следующих работах [1–10].
Рассмотрим устойчивость двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних узловых точек на равномерной прямоугольной сетке [3, 8, 9].
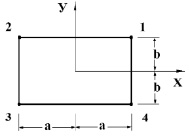
Рис. 1. Прямоугольный конечный элемент
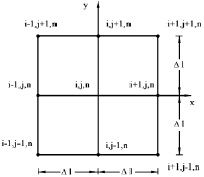
Рис. 2. Прямоугольная равномерная конечноэлементная сетка по пространственным координатам (шаблон из девяти точек)
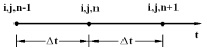
Рис. 3. Прямоугольная равномерная конечноэлементная сетка по временной координате
Используя основные соотношения для прямоугольного конечного элемента (рис. 1), покажем матрицу жесткости 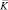 и вектор инерции для
и вектор инерции для 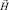 двумерного прямоугольного конечного элемента
двумерного прямоугольного конечного элемента
 (1)
(1)
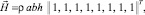 (2)
(2)
где
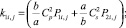
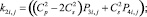
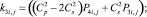
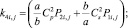
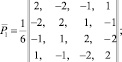
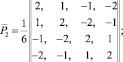
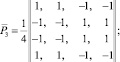

где E – модуль упругости; ν – коэффициент Пуассона; ρ – плотность материала; 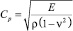 – скорость продольной упругой волны;
– скорость продольной упругой волны; 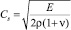 – скорость поперечной упругой волны; a – половина длины прямоугольного конечного элемента; b – половина высоты прямоугольного конечного элемента; h – толщина прямоугольного конечного элемента.
– скорость поперечной упругой волны; a – половина длины прямоугольного конечного элемента; b – половина высоты прямоугольного конечного элемента; h – толщина прямоугольного конечного элемента.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для некоторого деформируемого тела [1, 4–7], записываем приближенное значение уравнения движения в теории упругости
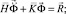
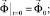
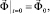 (3)
(3)
где 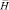 – матрица инерции;
– матрица инерции; 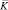 – матрица жесткости;
– матрица жесткости; 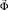 – вектор узловых упругих перемещений;
– вектор узловых упругих перемещений;  – вектор узловых упругих скоростей перемещений;
– вектор узловых упругих скоростей перемещений; 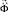 – вектор узловых упругих ускорений;
– вектор узловых упругих ускорений; 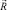 – вектор узловых упругих внешних сил.
– вектор узловых упругих внешних сил.
Соотношение (3) система линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями.
Таким образом, с помощью метода конечных элементов в перемещениях, линейную задачу с начальными и граничными условиями привели к линейной задаче Коши.
Интегрируя по временной координате соотношение (3) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек
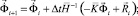
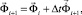 (4)
(4)
где Δt – шаг по временной координате.
Исследуем на устойчивость явные конечноэлементные линейные схемы в перемещениях для внутренних узловых точек на равномерных сетках с помощью метода Неймана [1–3, 8, 9].
Будем искать решение явных двухслойных конечноэлементных линейных схем в перемещениях для внутренних узловых точек на равномерных сетках в виде
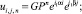 (5)
(5)
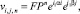 (6)
(6)
где 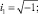 G и F – константы; P – функция целых чисел α и β.
G и F – константы; P – функция целых чисел α и β.
Рассмотрим устойчивость одномерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних узловых точек на равномерной прямоугольной сетке (рис. 2–3).
Рассмотрим уравнение динамического равновесия (4) для узловой точки (i, j, n) через элементы матрицы жесткости (1) и вектора инерции (2) конечного элемента с четырьмя узловыми точками:
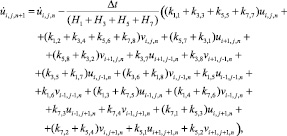 (7)
(7)
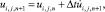 (8)
(8)
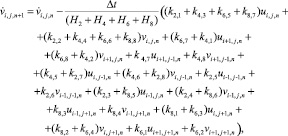 (9)
(9)
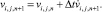 (10)
(10)
Подставляя (1–2) и (5–6) в (7–10), получаем систему при cos α = sin β = 1, которая имеет следующий вид:
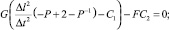 (11)
(11)
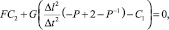 (12)
(12)
где
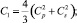
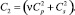
Из (11) и (12) получим матрицу
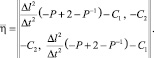 (13)
(13)
Раскрывая определитель матрицы 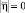 в (13), получим характеристическое уравнение
в (13), получим характеристическое уравнение
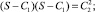 (14)
(14)
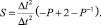 (15)
(15)
Из уравнений (14) и (15) получим
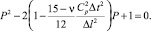 (16)
(16)
Устойчивость двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних узловых точек на равномерной прямоугольной сетке (4) будет иметь место, если шаг по временной координате подчинить условию
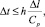 (17)
(17)
где
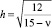 (0,83 < h < 0,89).
(0,83 < h < 0,89).
Выводы
1. Рассматривается исследование устойчивости двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних узловых точек на равномерной прямоугольной сетке. Применяется шаблон из девяти точек. С помощью метода конечных элементов дифференциальные уравнения в частных производных приведены к линейной задаче Коши с начальными условиями. С помощью конечноэлементного варианта метода Галеркина система обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями приведена к явной двухслойной конечноэлементной линейной схеме в перемещениях для внутренних и граничных узловых точек исследуемой области.
2. Аналитическое исследование устойчивости двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних узловых точек на прямоугольной сетке показало, что она удовлетворяет условию устойчивости Неймана.
3. Шаг по временной координате при различных значениях коэффициента Пуассона изменяется от 0,83 до 0,89, то есть он удовлетворяет условию Куранта.



