Допустим что, поток воздуха образует скоростной поезд со скоростью 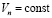
Целью рассматриваемой задачи является определение распределения скоростей потока воздуха и давление частиц воздуха в окружающем регионе (вокруг двигающихся вагонов поезда), а также коэффициент сопротивления движению поезда образованной за счет возмущения при движении поезда в безграничной воздушной среде.
Предполагается, что возникшее возмущенное движение воздуха потенциальное, стационарное. Рассматривается движение скоростного поезда дозвуковое и поэтому полагается учесть сжимаемость воздуха. Также предполагается, что на расстоянии 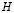 от боковой стенки поезда скорость частиц воздуха будет намного меньше, чем скорость поезда.
от боковой стенки поезда скорость частиц воздуха будет намного меньше, чем скорость поезда.
Ранее была решена аналогичная задача для воздушного потока в вертикальной плоскости [3]. Далее эту задачу решим для горизонтальной плоскости с целью определения поля скоростей в горизонтальной плоскости. Предполагается, что процесс в воздухе политропический, т.е. давление и плотность воздуха удовлетворяет закон политропии.
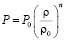 , (1)
, (1)
где P, r – давление и плотность частиц воздуха, 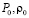 – давление и плотность частиц воздуха неподвижности и состояния (параметры торможения), n – показатель политропии.
– давление и плотность частиц воздуха неподвижности и состояния (параметры торможения), n – показатель политропии.
В работе [1] предложен метод решения задачи о течении сжимаемой жидкости с образованием свободной поверхности или поверхности при дозвуковом течении жидкостей. Получены выражения для давления, плотности давления и температуры. При существовании интеграла Бернулли [1] в виде
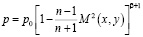 (2)
(2)
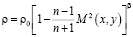 , (3)
, (3)
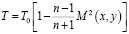 , (4)
, (4)
полагается, что
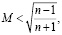
где 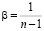 ,
, 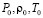 – параметры воздуха в положении равновесия, n – показатель политропии,
– параметры воздуха в положении равновесия, n – показатель политропии, 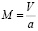 – число Маха, a – скорость распространения малых возмущений в воздухе,
– число Маха, a – скорость распространения малых возмущений в воздухе, 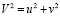 где u, v – компоненты вектора
где u, v – компоненты вектора 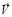 скорости частиц воздуха.
скорости частиц воздуха.
Для решения этой задачи, ниже рассмотрим струйную модель Кирхгофа, где отсутствуют кавитации.
Поскольку в определенном расстоянии от линии 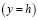 скорость частиц воздуха возникшее за счет движения поезда становятся малым, а при
скорость частиц воздуха возникшее за счет движения поезда становятся малым, а при 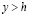 скорости частиц воздуха становятся равным нулю, поэтому за модель струйного течения воздуха, применим модель Кирхгоффа-Гельмгольца. С увеличением скорости поезда как впереди, так и сзади поезда возникают зоны отрыва, более сложные струйные модели Тулина, Лаврентьева, Эфроса, Жуковского, Чаплыгина и другие (см. [1]).
скорости частиц воздуха становятся равным нулю, поэтому за модель струйного течения воздуха, применим модель Кирхгоффа-Гельмгольца. С увеличением скорости поезда как впереди, так и сзади поезда возникают зоны отрыва, более сложные струйные модели Тулина, Лаврентьева, Эфроса, Жуковского, Чаплыгина и другие (см. [1]).
Ниже рассматриваемая задача предварительно решается. Для случая когда воздух несжимаем, т.е. когда число Маха удовлетворяет условию 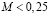 . Далее пользуясь этим решением, определяется поле скоростей для случая,
. Далее пользуясь этим решением, определяется поле скоростей для случая, 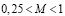 т.е. дозвуковой скорости.
т.е. дозвуковой скорости.
Областью движения воздуха будет Gz ограниченные твердыми границам AB, BC, CD и E – и свободная поверхность DE. Поскольку свободная поверхность DE форма которой определяются в процессе решения.
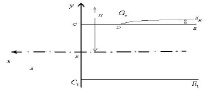
Рис. 1
В зависимости от скорости поезда точка отрыва потока воздуха с поверхности поезда сдвигается к точке C рис. 1.
Введем область G0 действительная ось области G0 (при 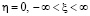 ) соответствуют границе области течения Gz. Для этого предварительно задача решается в канонической области G0, а далее определяется функция
) соответствуют границе области течения Gz. Для этого предварительно задача решается в канонической области G0, а далее определяется функция 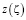 , которая дает конформное отображение области G0 в область течения Gz, определяемое процессе решения задачи.
, которая дает конформное отображение области G0 в область течения Gz, определяемое процессе решения задачи.
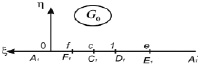
Рис. 2
Постановка задачи вдоль области A1, F1, C1, D1, E1, где заданы мнимая часть функции 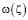 . Полагаются отрезки границы A1F1, F1C1, C1D1, D1E1 и
. Полагаются отрезки границы A1F1, F1C1, C1D1, D1E1 и 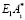 области G0, соответствуют границам AB, BC, CD, DE и EA соответственно; а также точки находящие в этих отрезках G0 соответственно к точкам границ в области Gz.
области G0, соответствуют границам AB, BC, CD, DE и EA соответственно; а также точки находящие в этих отрезках G0 соответственно к точкам границ в области Gz.
Для решения рассматриваемой задачи введем функции потенциала скорости 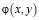 , функцию тока
, функцию тока 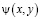 и комплексный потенциал
и комплексный потенциал
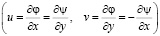
в виде:
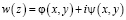 . (5)
. (5)
При M<1, введенная функция будет аналитической функцией в области течения Gz (рис. 3) и области G0 (рис. 2).
Для решения задачи введем функцию Жуковского 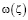 определяемой равенством
определяемой равенством
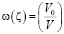 , (6)
, (6)
где 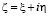 , V0 – скорость частиц воздуха, где
, V0 – скорость частиц воздуха, где 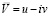 сопряженная комплексная скорость. Вдоль свободной поверхности DE; а также вдоль EA реальная часть функции Жуковского в связи с этим введем
сопряженная комплексная скорость. Вдоль свободной поверхности DE; а также вдоль EA реальная часть функции Жуковского в связи с этим введем 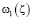 в виде:
в виде:
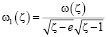 . (7)
. (7)
Тогда во всех участках действительной оси G0 заданы лишь мнимая часть искомой функции 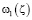 , где
, где 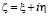 (при
(при 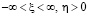 ).
).
Для решения задачи в области G0 (рис. 2) из равенства (7) установим следующие граничные условия вдоль действительной оси в области 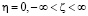 .
.
Для этих функций имеем следующие граничные условия:
Вдоль отрезка
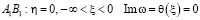
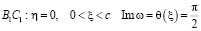
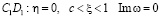
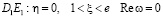
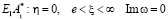
Введенная функция
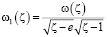 ,
,
граничные условия для функции 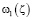 будут:
будут:
Вдоль отрезка
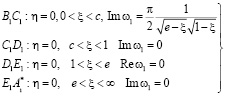 . (8)
. (8)
Пользуясь интегральной формулой Шварца, получим выражение для аналитической функции 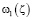 в области G0 в виде
в области G0 в виде
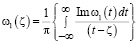 . (9)
. (9)
Учитывая условия (2.8), на действительной оси области G0 имеем
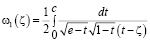 .
.
Интегрируя по x, будем иметь следующие выражении для искомой функции
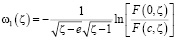 . (10)
. (10)
Учитывая равенство (1.37) находим
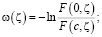 (11)
(11)
где 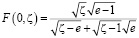 ; (12)
; (12)
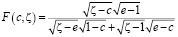 .(13)
.(13)
Обозначим
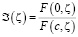 . (14)
. (14)
Из равенств (6) и (14) имеем распределения сопряженной комплексной скорости в области G0 в виде
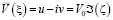 , (15)
, (15)
где 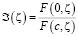 .
.
Для получения поля скоростей в области течение Gz определим функцию отображения 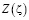 областей G0, Gz. Поскольку функции комплексного потенциала
областей G0, Gz. Поскольку функции комплексного потенциала 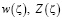 аналитические функции в области G0, имеем:
аналитические функции в области G0, имеем:
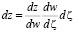
интегрируя по 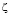 , получим искомую функцию отображения:
, получим искомую функцию отображения:
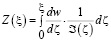 . (16)
. (16)
Поскольку в области G0 источник с расходами q расположен в точке A 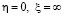 , а стока в точке Е, то для комплексного потенциала в области G0, имеем
, а стока в точке Е, то для комплексного потенциала в области G0, имеем
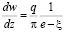 ; (17)
; (17)
где q – секундный расход в источнике и стоке 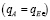 потеря жидкости в области G0 и Gz определяемое равенством
потеря жидкости в области G0 и Gz определяемое равенством 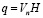 отсутствуют. Полагая,
отсутствуют. Полагая, 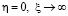 определим зависимость между скоростью на струе DE и скоростью поезда Vn:
определим зависимость между скоростью на струе DE и скоростью поезда Vn:
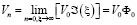 ,
,
так что скорость частиц воздуха на свободной поверхности DE определяется равенством
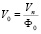 , (18)
, (18)
где 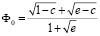 ; (19)
; (19)
Равенство (14) дает поле скоростей в области G0, а равенство (16) дает функцию, определяющую точки областей G0 и Gz, учитывая равенства (16) и (17) получим аналитическое выражения для искомой функции отображения
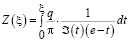
или
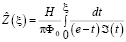 , (20)
, (20)
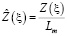 ,
,
где 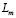 – ширина вагона, а равенства (14) и (20) дают поле скоростей частиц воздуха в области течения Gz.
– ширина вагона, а равенства (14) и (20) дают поле скоростей частиц воздуха в области течения Gz.
В случае сжимаемой жидкости, действуем приближенным методом, изложенным в работе [1].
В функциях 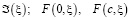 входят неизвестные параметры, определяемые равенствами c и e из двух условий. Равенство длины отрезка
входят неизвестные параметры, определяемые равенствами c и e из двух условий. Равенство длины отрезка 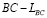 – заданной
– заданной
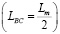 ,
,
где Lm – ширина вагона поезда и условия равенства расходов в источнике (А) и стоке (Е) 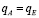 , известно
, известно
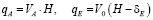 ; (21)
; (21)
где 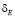 – отклонение свободной поверхности от боковых стенок вагонов.
– отклонение свободной поверхности от боковых стенок вагонов.
Распределения скоростей вдоль свободной поверхности CD определяется равенствами (20),
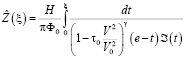
и
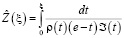 ,
,
где 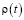 определяется из (3).
определяется из (3).
Из равенства (16) и (14) с учетом равенства (2) получим выражение
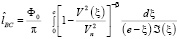 .(22)
.(22)
Далее определим ширину в стоке, следующим равенством: 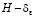 ,
,
где
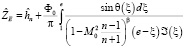 (23)
(23)
где 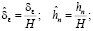 толщина струи в точке E определяется равенством
толщина струи в точке E определяется равенством
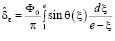 ; (24)
; (24)
где 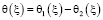 ,
,
а 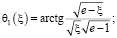
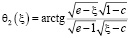 , (25)
, (25)
так что, из равенства расходов в источнике и стоке 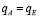 будем, иметь:
будем, иметь:
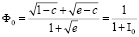 , (26)
, (26)
где
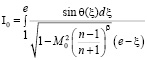 ;
;
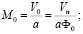
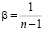 ;
; 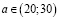
для воздуха 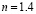 .
.
Равенства (22), (24) и
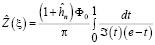 ; (27)
; (27)
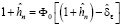
будут системой уравнений для определения 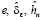 и c. Так же должно удовлетворяться условию
и c. Так же должно удовлетворяться условию
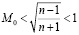 .
.



