Импульсное воздействие характеризуется внезапностью приложения и кратковременностью действия, измеряемого микросекундами. Интенсивность их достаточно велика, для того чтобы произвести разрушение и большие необратимые изменения в теле, на которые они действуют.
В деформируемом теле при импульсном воздействии возникают возмущения различной природы. Они распространятся с конечными скоростями. Величина возмущений зависит от состояния тела и характера деформаций, в виде волн возмущений, называемых волнами напряжений. Возмущения, распространяясь в теле, образуют области, которые расширяются с течением времени и ограничены частью поверхности тела и поверхностью фронта волны напряжений.
Каждой области возмущений соответствует свое напряженно-деформированное состояние, характеризуемое тензором напряжений и тензором деформаций. Области возмущений можно разделить на первичные и вторичные. Первичной является область возмущений волны нагрузки. Области возмущений волн разгрузки и отраженных будут вторичными. Они всегда находятся внутри области возмущений волны нагрузки и являются областями с начальными напряжениями и деформациями.
Волны напряжений различной природы, распространяясь, в деформируемом теле взаимодействуют, друг с другом, что приводит к образованию новых областей возмущений, перераспределению напряжений и деформаций.
Напряженное состояние волнового нагруженного тела может изменяться так быстро, что возникающие деформации и разрушения еще не успевают распространиться, как распределение напряжений изменится, так как скорости распространения волн напряжений достигают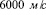 
, а нарушение прочности распространяются со скоростью не более 
.
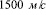При интерференции волн напряжений их интенсивности складываются. Они могут достигать значений, превосходящих предел прочности материала. В этом случае наступает разрушение материала.
После трехкратного или четырехкратного прохождения и отражения волн напряжений в теле процесс распространения возмущений становится установившимся, напряжения и деформации усредняются, тело находится в колебательном движении.
Некоторые вопросы в области постановки, разработки методики, алгоритма и результаты решенных нестационарных динамических задач рассмотрены в следующих работах [1–10].
Постановка задачи
Для решения поставленной задачи рассмотрим некоторое тело Г (рис. 1) в прямоугольной декартовой системе координат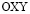 
, которому в начальный момент времени 
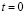сообщается механическое воздействие.
Точные уравнения двумерной (плоское напряженное состояние) динамической теории упругости имеют вид
, 
,
,
,
,
,
, 
,
, 
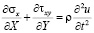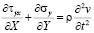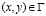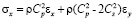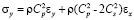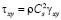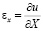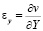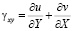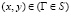, (1)
где 
, 
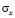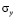и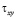 
– компоненты тензора упругих напряжени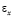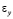й; 
, 
и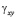 
– компоненты тензора упругих деформаци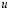й; 
и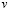 
– cоставляющие вектора упругих перемещений вдоль осе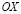й 
и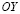 
соответственно; r – плотность материала; 
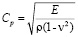– скорость продольной упругой волны; 
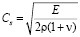– скорость поперечной упругой волны; 
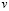– коэффициент Пуассона; 
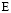– модуль упругости; 
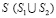– граничный контур тела 
.
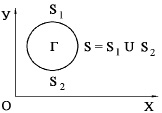
Рис. 1. Некоторое тело Г в прямоугольной декартовой системе координат 
Систему (1) в области, занимаемой телом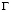 
, следует интегрировать при начальных и граничных условиях.
Начальные условия в области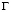 
зададим в виде
, 
, 
,
, 
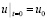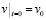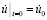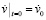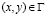, (2)
где 
, 
, 
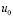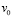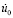и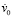 
– заданные в области 
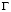функции.
Граничные условия зададим в виде:
составляющих компонентов тензора упругих напряжений на границе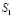 
, 
,
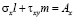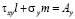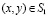; (3)
составляющих компонентов вектора упругих перемещений на границе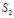 
, 
, 
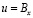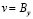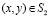, (4)
где l и m – направляющие косинусы;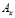 
, 
, 
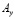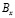и 
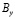– заданные на границе S функции.
Разработка методики и алгоритма
Для решения двумерной нестационарной динамической задачи математической теории упругости с начальными и граничными условиями (1–4) используем метод конечных элементов в перемещениях [1, 4, 6].
Задача решается методом сквозного счета, без выделения разрывов. Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела <<mus58.wmf>>, записываем приближенное значение уравнения движения в теории упругости
, 
,
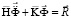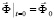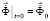, (5)
где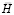 
– матрица инерции; 
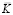– матрица жесткости; 
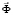– вектор узловых упругих перемещений; 
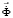– вектор узловых упругих скоростей перемещений; 
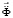– вектор узловых упругих ускорений; 
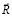– вектор узловых упругих внешних сил.
Соотношение (5) система линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями.
Таким образом, с помощью метода конечных элементов в перемещениях, линейную задачу с начальными и граничными условиями (1–4) привели к линейной задаче Коши (5).
Для интегрирования уравнения (5) конечноэлементным вариантом метода Галеркина приведем его к следующему виду
, 
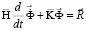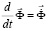. (6)
Интегрируя по временной координате соотношение (6) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек
,
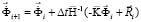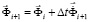. (7)
где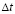 
– шаг по временной координате.
Определим упругое контурное напряжение на границе области, свободной от нагрузок.
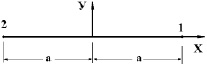
Рис. 2. Контурный конечный элемент с двумя узловыми точками
С помощью вырождения прямоугольного конечного элемента с четырьмя узловыми точками получим контурный конечный элемент с двумя узловыми точками (рис. 2).
При повороте оси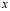 
на угол 
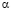против часовой стрелки, получим упругое контурное напряжение 
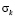в центре тяжести контурного конечного элемента с двумя узловыми точками
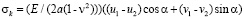. (8)
Рассмотрим устойчивость двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних и граничных узловых точек на квазирегулярных сетках
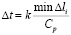
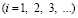, (9)
где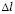 
– длина стороны конечного элемента.
Результаты численного эксперимента показали, что при k = 0,5 обеспечивается устойчивость двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних и граничных узловых точек на квазирегулярных сетках.
Для исследуемой области, состоящей из материалов с разными физическими свойствами, выбирается минимальный шаг по временной координате.
На основе метода конечных элементов в перемещениях разработаны алгоритм и комплекс программ для решения линейных плоских двумерных задач, которые позволяют решать сложные задачи при нестационарных динамических воздействиях на уникальные сооружения [1, 5–10].
При разработке комплекса программ использовался алгоритмический язык Фортран-90.
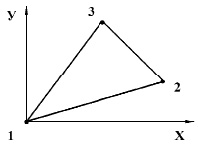
Рис. 3. Треугольный конечный элемент с тремя узловыми точками
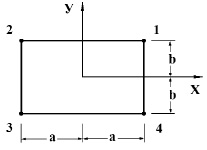
Рис. 4. Прямоугольный конечный элемент с четырьмя узловыми точками
Исследуемая область разбивается по пространственным переменным на треугольные конечные элементы с тремя узловыми точками с линейной аппроксимацией упругих перемещений (рис. 3) и на прямоугольные конечные элементы с четырьмя узловыми точками с билинейной аппроксимацией упругих перемещений (рис. 4). По временной переменной исследуемая область разбивается на линейные конечные элементы с двумя узловыми точками с линейной аппроксимацией упругих перемещений.
Выводы
Для моделирования волн напряжений в деформируемых областях сложной формы применяется численное моделирование. На основе метода конечных элементов в перемещениях разработаны методика, алгоритм и комплекс программ для решения линейных двумерных плоских задач, которые позволяют решать сложные задачи при ударных воздействиях на сооружения. Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений. Матрица упругости выражена через скорость продольных волн, скорость поперечных волн и плотность.
Исследуемая область разбивается по пространственным переменным на треугольные конечные элементы с тремя узловыми точками с линейной аппроксимацией упругих перемещений и на прямоугольные конечные элементы с четырьмя узловыми точками с билинейной аппроксимацией упругих перемещений. По временной переменной исследуемая область разбивается на линейные конечные элементы с двумя узловыми точками с линейной аппроксимацией упругих перемещений. За основные неизвестные приняты два перемещения и две скорости перемещений в узле конечного элемента.
Задачи решаются с методом сквозного счета, без выделения разрывов. Применяется кусочно-линейная аппроксимация для уменьшения влияния разрывных на точность результатов численного решения, полученных с помощью метода конечных элементов в перемещениях.
Линейная динамическая задача с начальными и граничными условиями в виде дифференциальных уравнений в частных производных, для решения задач о нестационарных воздействиях на деформируемые объекты сложной формы, с помощью метода конечных элементов в перемещениях приведена к системе линейных обыкновенных дифференциальных уравнений с начальными условиями, которая решается по явной двухслойной схеме.