Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Важным условием устойчивого развития финансовой системы Казахстна является обеспечение финансовой устойчивости коммерческих организаций, поддержание в долгосрочном аспекте оптимальной структуры источников их финансирования. Обеспечение финансовой устойчивости представляет собой трудоемкий процесс анализа, мониторинга и прогнозирования ее основных показателей, а также реализации мероприятий по результатам выявленных отклонений.

С целью совершенствования управления финансовой устойчивостью казахстанских предприятий в условиях рыночной экономики необходимо повысить требования к ее обеспечению, предложить инструментарий, который позволит прогнозировать ее уровень и риски снижения финансовой устойчивости на ранней стадии диагностики.

Несомненная важность и недостаточная изученность многоаспектных проблем анализа и многофакторных методов прогнозирования финансового состояния, необходимость формирования прогнозно-аналитической системы, позволяющей получать реальную и потенциальную оценку эффективности деятельности коммерческих организаций, и установление ее составных компонентов, определяют актуальность данных исследований [1].

В разной степени изучению этих проблем посвящены работы многих известных ученых и экономистов: М.И. Баканова, С.Б. Барнгольц, М.А. Бахрушиной, Н.В. Парушиной, Г.В. Савицкой, С.Г. Чеглаковой, М.Б. Чирковой, А.Д. Шеремета С.Дж. Брауна, Ю.Ф. Брикхэма, М. Вебера, М.А. Гольцберга, Т.Р. Карлина, А.Р. Макмина и др.

Прогнозирование финансовой устойчивости коммерческой организации представляет совокупность аналитических процедур, применяемых для диагностики финансовой устойчивости хозяйствующего субъекта в перспективе посредством разработанных методик анализа и прогнозирования финансовой устойчивости на основе действующей методологии (методов и приемов) экономического анализа и прогнозирования. Значение прогнозирования финансовой устойчивости заключается в информационном обеспечении процесса управления финансами коммерческой организации.

В настоящее время разработано большое число различных моделей, направленных на определение прогнозной величины финансовой устойчивости предприятия. Большинство моделей строятся на основе тренда ряда индикаторов выявляются признаки тенденций развития финансового положения предприятия. Однако функционирование любой экономической системы происходит в условиях сложного взаимодействия комплекса внутренних и внешних факторов [1, 2].

При изучении закономерностей экономических явлений большое значение имеет выявление связей между взаимосвязанными, развивающимися во времени явлениями, проведение связанного анализа динамики. С этой целью строятся многофакторные модели взаимосвязанных временных рядов.

Под факторным анализом понимается методика комплексного и системного изучения и измерения воздействия факторов на величину результативных показателей.

Многофакторной моделью называют модель, построенную по нескольким временным рядам, уровни которых относятся к одинаковым временным отрезкам или датам. При моделировании многомерных временных рядов особое значение имеет корреляционный и регрессионный анализ. Моделирование связных рядов динамики основано на использовании уравнений регрессии. Подобные модели отображают сложившиеся между исследуемыми показателями взаимосвязи с достаточной степенью точности и позволяют оценить степень влияния отдельных факторов на результативный признак, а также эффективность влияния всех факторных признаков.

Методика. Как показали исследования, описанные в работах разных авторов, результаты прогнозов экономических процессов по модели, построенной по рядам динамики, вполне удовлетворительные. Поэтому представляется целесообразным более подробно рассмотреть именно эту методику построения динамической модели многофакторного прогнозирования [3, 4].

Для каждого года l изучаемого периода L строится многофакторная модель с учетом исключения мультиколлинеарности и обоснования аналитического вида модели. Необходимо, чтобы оценки главного фактора были несмещенными, состоятельными и эффективными на рассматриваемом отрезке времени. Запишем в виде линейной модели:

;

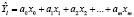где Yl – моделируемый показатель l гоa года; xi – факторы, влияющие на данный показатель, i = 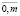; ai – параметры модели, i = 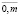; m – число факторных признаков.

Получаем систему из L таких моделей, каждая из которых проверяется на адекватность по F-критерию и t-критерию. Для прогнозирования зависимой переменной (результативного признака) на L шагов вперед необходимо знать прогнозные значения всех входящих в модель факторов. Эти значения могут быть получены на основе трендовых моделей, например, с использованием метода экстраполяции или непосредственно заданы исследователем экономического процесса. Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.

Для определения области возможных значений результативного показателя при известных значениях факторов, т.е. доверительного интервала прогноза, необходимо учитывать два возможных источника ошибок. Ошибки первого рода вызываются рассеиванием наблюдений относительно линии регрессии, и их можно учесть, в частности, величиной среднеквадратической ошибки изучаемого показателя с помощью регрессионной модели 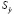. Ошибки второго рода обусловлены тем, что заданные в модели коэффициенты регрессии являются случайными величинами, распределенными по нормальному закону. Эти ошибки учитываются вводом поправочного коэффициента при расчете ширины доверительного интервала; формула для его расчета включает табличное значение t-статистики при заданном уровне значимости и зависит от вида регрессионной модели.

Основная часть. Для разработки модели оптимизации финансовой устойчивости в работе используем метод корреляционно-регрессионного анализа. Корреляция представляет вероятную зависимость между показателями не находящимися в функциональной зависимости. Данный метод используется для определения тесноты связи между показателями финансовой устойчивости [3].

Для этого введем следующие обозначения: х1 – коэффициент автономии; х2 – коэффициент финансового риска; х3 – коэффициент долга; х4 – коэффициент финансовой устойчивости; х5 – коэффициент маневренности; х6 – коэффициент обеспеченности собственными оборотными средствами.

Составляем экономическую модель множественной регрессии в виде:

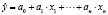
определим оценки а0, а1, … , аn параметров по методу наименьших квадратов (МНК).

Коэффициенты аi – показывают, на сколько измениться результативный показатель при изменении факторного на единицу.

На основании изложенного выделяем основные целевые показатели финансовой устойчивости хозяйствующего субъекта, которые считаем необходимым учитывать при построении модели прогнозирования.

Необходимые исходные данные берём из табл. 1 и рассчитываем параметры уравнения регрессии.

Таблица 1

Параметры уравнения регрессии

* Таблица составлена автором на основе расчета.

Составляем экономическую модель по данным табл. 1 и получаем систему многофакторных моделей формирующих показатель коэффициента финансовой устойчивости:

y = a0 + x2 a1

x2 = a0 + x1 a1 + x6 a2

x1 = a0 + x3 a1

x6 = a0 + x4 a1 + x5 a2

Таким образом, решается задача максимизации показателя y при заданных ограничениях, то есть, находим оптимальное решение коэффициента финансовой устойчивости для предприятия при варьировании значениями других коэффициентов.

Оценки а0, а1, а2 рассчитываем по МНК:

Уравнение регрессии с оценками параметров имеет вид:

.

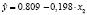Совокупный коэффициент множественной корреляции ry характеризует тесноту связи результативного y и факторных х1, х2, … , хm признаков и в общем случае определяется по формуле:

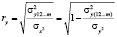, (1)

где 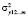– факторная дисперсия; 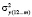– остаточная дисперсия; 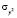– дисперсия результативного признака:

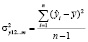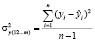; ; (2)

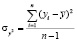(3)

где 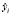– расчетное значение результативного признака; 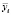– среднее значение результативного признака.

Приведенная форма записи индексов трактуется следующим образом: 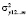– дисперсия 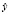, полученная с учетом факторов х1, х2, … , хm; 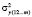– дисперсия 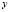, полученная с учетом факторов х1, … , хm;

Чем плотнее фактические значения 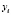располагаются относительно линии регрессии, тем меньше остаточная дисперсия (больше факторная дисперсия) и, следовательно, больше величина .

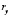Таким образом, коэффициент множественной корреляции, как и величина остаточной дисперсии, характеризует качество подбора уравнения регрессии.

Квадрат величины 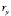является коэффициентом множественной детерминации и характеризует долю влияния выбранных признаков на результативный фактор:

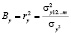. (4)

По данным сквозного примера имеем:

; ;

;

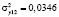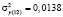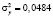
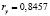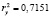
В соответствии с таблицей Чеддока связь результативного признаков считается высокой (0,71). Регрессия у на х1 объясняет на 71 % изменение показателя: Коэффициент долга.

Значение коэффициентов находится в пределах 0 ≤ ry ≤ 1.

При отсутствии связи между результативными и факторными признаками факторная дисперсия равна нулю, коэффициент множественной корреляции равен нулю и линия регрессии совпадает с прямой 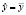. При функциональной связи факторная дисперсия совпадает с общей дисперсией, а коэффициент корреляции равен 1.

Оценка значимости коэффициента детерминации определяется с использованием критерия Фишера. По данным проводимых расчетов критерий Фишера имеет следующее значение:

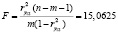(5)

По таблице F-распределения находим для степеней свободы f1= m = 2 и f2= n – m – 1 = 7 – –2 – 1 = 4 , a = 5 % , Fкр = 5,32 , и, следовательно, значение коэффициента детерминации и значение коэффициента множественной корреляции являются значимыми (F > Fкр).

Для оценки вклада во множественный коэффициент корреляции каждого из факторов применяют частные коэффициенты корреляции.

Частный коэффициент корреляции – это показатель, характеризующий тесноту связи между признаками при элиминации всех остальных признаков. В общем случае формула для определения частного коэффициента корреляции между факторами у и х при элиминации влияния факторов х1, …, хm-1 имеет вид:

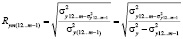(6)

где 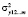– факторная дисперсия регрессии у на х1, х2, … , хm; 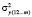– факторная дисперсия у, полученная с учетом факторов х1, … , хm-1; 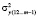– остаточная дисперсия регрессии у, полученная с учетом факторов х1, х2, … , х; 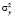–дисперсия результативного фактора.

Величина частного коэффициента корреляции лежит в пределах от 0 до 1, а знак определяется знаком соответствующих параметров регрессии.

Принимая вместо σ2 его оценку S2:

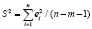, (7)

где n – число наблюдений; m – число объясняющих переменных.

Тогда

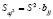, (8)

где bjj – диагональные элементы матрицы оценки параметров уравнения регрессии.

Квадратическая ошибка 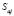равна:

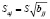. (9)

Полученные квадратические ошибки могут быть использованы для расчета доверительных интервалов оценок параметров регрессии и для проверки значимости их отличия от нуля.

Учитывая, что 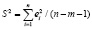, имеем:

S = 0,4625;

S a0 = 0,0998;

S a1 = 0,0511.

Расчетный критерий ti равен:

; .

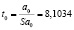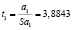Для доверительной вероятности р=0,95 и числа степеней свободы k=8 по таблице Стьюдента находим tкр = 2,57. Поэтому критерию в уравнении регрессии значимыми являются все параметры: а0, а1, а2.

t0 = 8,1034 > tкр = 2,57;

t1 = 3,8834 > tкр = 2,57.

Таблица 2

Прогнозные значения коэффициента финансовой устойчивости на период 2013-2016 гг.

* Таблица составлена автором на основе расчета.

Для остальных финансовых показателей экономикой модели разработаны ряд многофакторных моделей и получены следующие расчетные характеристики этих уравнений.

Таблица 3

Прогнозные значения коэффициента долга на период 2013-2016 гг.

* Таблица составлена автором на основе расчета.

Таблица 4

Прогнозные значения коэффициента финансового риска (коэф. задолженности, соотношения заемных и собственных средств, рычага) на период 2013-2016 гг.

* Таблица составлена автором на основе расчета.

Таблица 5

Прогнозные значения коэффициента обеспеченности оборотного капитала собственными источниками финансирования на период 2013-2016 гг.

* Таблица составлена автором на основе расчета.

Проанализируем цифровые данные, приведенные в списке многофакторных регрессионных уравнений. В целом прогнозные значения, полученные на основе решения многофакторных регрессионных уравнений и прогнозные значения, рассчитанные на основе одинарных уравнений регрессии от временного тренда, имеют более доверительное предпочтение, так как последние в большинстве случаев отражают только трендовую перспективу развития, хотя и находятся в пределах допустимой погрешности.

Уравнение Y = 0.809 – 0.198 X2 свидетельствует о снижении коэффициента финансовой устойчивости на 0,198 единиц ( далее – ед.) в случае повышения X2 – коэффициента долга на 1,0 ед. Уравнение X2 = 1.760 – 2.154 X1 + 5.584 X6 также свидетельствует о том, что коэффициент долга меняет свое значение на 1,0 ед под воздействием изменения параметров коэффициента финансового риска на 2,154 ед. и коэффициента обеспеченности оборотного капитала собственными источниками финансирования на 5,584 ед.

В случае снижения коэффициента автономии на 1,0 ед., согласно уравнения X1 = 0.556 – 0.204 X3 происходит снижение коэффициента финансового риска на 0,204 ед.

Уравнение X6 = – 0.270 – 0.637 X4 + 2.323 X5 показывает зависимость коэффициента обеспеченности оборотного капитала собственными источниками финансирования от коэффициента маневренности собственных средств на 0,637 ед. и коэффициента устойчивости структуры мобильных средств на 2,323 ед.

Выводы. Таким образом, прогнозные значения, полученные по системе многофакторных регрессионных уравнений, могут служить основой для индикативного планирования финансовой стратегии развития предприятия на соответствующие годы. Отклонения вполне допустимые, если учесть структуру исходных статистических рядов.

При стремлении максимизировать значение коэффициента финансовой устойчивости, который является основным из рыночных коэффициентов финансовой устойчивости, полученные прогнозные значения свидетельствуют о том, что у предприятия коэффициент финансового риска и долга должен быть приближен или равен нулю. Коэффициент маневренности при этом имеет тенденцию к снижению, что свидетельствует о не гибком использовании собственных источников. Данные решения вполне реализуемы и применимы на практике, в случае привлечения заемные средств, необходимых для нормальной работы предприятия.

Таким образом, при правильном пользовании коэффициентами финансовой устойчивости можно активно воздействовать на уровень финансовой устойчивости, повышать его до минимально необходимого, а если он фактически превышает минимально необходимый уровень, – использовать эту ситуацию для улучшения структуры активов и пассивов.