Математический аппарата дискретного преобразования Фурье (ДПФ) и быстрого преобразования Фурье (БПФ) нашли широкое применение в алгоритмах цифровой обработки сигналов (ЦОС). При этом цифровая обработка сигналов характеризуется обработкой большого объема данных в реальном масштабе времени. Обеспечить выполнение данного условия возможно за счет использования непозиционных модулярных кодов.
Одним из основных критериев цифровой обработки сигналов является необходимость выполнения ортогональных преобразований в реальном масштабе времени. Для решения данной проблемы предлагается использовать непозиционные модулярные коды. Так в работах [1-3] для проведения ортогональных преобразований сигналов предлагается использовать систему остаточных классов (СОК). В данной непозиционной системе счисления в качестве оснований используются взаимнопростые числа 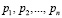 , у которых
, у которых
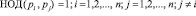 .
.
Тогда любое число, которое не превосходит рабочий диапазон СОК, можно представить в виде набора остатков, полученных при делении этого числа на числа-основания
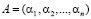 , (1)
, (1)
где 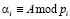 ;
; 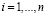 .
.
В качестве основного достоинства системы остаточных классов можно отметить высокую скорость выполнения модульных операций [1]. Этими операциями являются операции сложение, вычитание и умножение.
Пусть дана пара чисел А и В, которая представлена в модулярном непозиционном коде 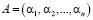 и
и 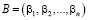 . Тогда операции сложения, вычитания и умножения по модулю можно представить соответствующими операциями над остатками
. Тогда операции сложения, вычитания и умножения по модулю можно представить соответствующими операциями над остатками
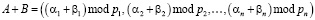 . (2)
. (2)
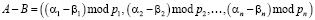 . (3)
. (3)
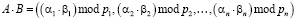 . (4)
. (4)
Тогда, используя систему остаточных классов, можно реализовать ортогональные преобразования сигналов в виде n параллельно выполняемых вычислений дискретного преобразования Фурье по основаниям СОК
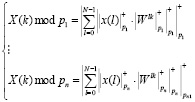 . (5)
. (5)
где Wlk – поворачивающий коэффициент; k =0,1,2,…,N–1; 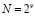 .
.
Следует отметить, что математический аппарат непозиционного кодирования класса вычетов эффективно поддерживает также реализацию БПФ. Так при использовании параллельно-конвейерного алгоритма БПФ выражение (5) принимает вид
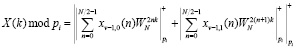 . (6)
. (6)
где 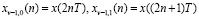 – соответственно последовательность с четными и нечетными номерами;
– соответственно последовательность с четными и нечетными номерами; 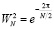 .
.
При этом, несмотря на необходимость проведения прямого преобразования из позиционного кода в модулярный код и ему обратного преобразования, спецпроцессор БПФ класса вычетов позволяет в производительность. Сравнительный анализ времени выполнения БПФ в позиционной системе счисления (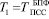 ) и с использованием параллельных вычислений (
) и с использованием параллельных вычислений (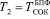 ) показан на рисунке. Для оценки был выбран относительный коэффициент
) показан на рисунке. Для оценки был выбран относительный коэффициент 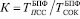 .
.
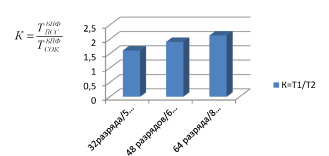
Сравнительный анализ времени выполнения БПФ в ПСС (Т1) и в СОК (Т2)
Анализ данного рисунка показывает, что применение СОК позволяет повысить скорость цифровой обработки сигналов с использованием алгоритма БПФ более чем в 1,5 раза при обработке уже 32 разрядных данных. Причем при увеличении разрядности обрабатываемых данных выигрыш возрастает. Так при обработке 64 разрядных данных скорость непозиционного процессора более чем в 2 раза превосходит скорость работы позиционного СП ЦОС, даже с учетом необходимости выполнения операций прямого и обратного преобразований кодов.
Наряду с системой остаточных классов в ряде работ предлагается использовать для проведения ортогональных преобразований сигналов – кольцо полиномов. В этом случае осуществляется переход от одномерной обработки сигнала к многомерной. Использование данного математического аппарата в задачах ЦОС достаточно наглядно приведено в работах [4-8]. В отличие от СОК данный непозиционный модулярный код образуется с помощью неприводимых полиномов 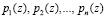 , у которых
, у которых
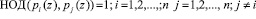 .
.
Использование полиномиальной системы классов вычетов (ПСКВ) позволяет осуществлять ортогональные преобразования на основе целочисленной арифметике, обладающей минимальными погрешностями точности вычислений
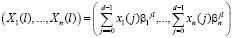 , (7)
, (7)
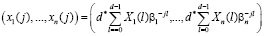 , (8)
, (8)
где 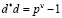 .
.
При этом справедливо
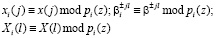 (9)
(9)
Если приравнять соответствующие координаты, получаем n пар прямого преобразования
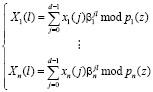 , (10)
, (10)
и n пар обратного преобразования
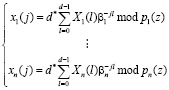 . (11)
. (11)
Применение выражений (10) и (11) позволяет свести вычисление ортогональных преобразований сигналов над кольцом Р(z) к n независимым вычислениям, проводимым по модулям pi(z) кода ПСКВ. При этом обеспечить повышение скорости цифровой обработки сигналов в кодах ПСКВ возможно за счет использования параллельно-конвейерных вычислений и быстрых алгоритмов с матрицами меньшей размерности [5-6]. Однако ДПФ и БПФ в своем традиционном виде не способны осуществлять анализ нестационарных сигналов. Следовательно, для спектрального анализа реальных сигналов необходимо использовать вейвлет-преобразования.
В настоящее время вейвлет-преобразования нашли широкое применение благодаря тому, что преобразование Фурье и его быстрые алгоритмы неэффективно обеспечивают анализ нестационарных сигналов, которые локализованы в некотором интервале времени. Это связано с тем, что при ортогональных преобразованиях ДПФ и БПФ теряется информация о сигнале во временной области. Следовательно, для получения истинной картины при анализе сигнала необходимо производить эту процедуру как во временной области, так и в частотной области. Это позволит наиболее правильно оценить изменения частотно-временных характеристик сигнала.
Известно, что частотно-временной анализ предназначен для выявления локальных частотно-временных возмущений сигнала. При этом различают два вида вейвлет-преобразований:
– непрерывное вейвлет-преобразование;
– дискретное вейвлет-преобразование.
Представление функции f(t) через ее непрерывное вейвлет преобразование является избыточным. Это связано с тем, что обрабатываемые сигналы имеют ограниченную полосу и энергию. Кроме того, при преобразовании аналогового сигнала к цифровой форме допускает определенный вид погрешности квантования. Поэтому на практике наибольшее применение нашли дискретные вейвлет-преобразования.
В настоящее время существует целый ряд вейвлетов, которые используются при крупномасштабном анализе сигналов. Наибольшее применение нашли вейвлеты Добеши [9, 10]. Семейство вейвлетов Добеши состоит из ортонормальных функций с компактным носителем, в котором каждая следующая функция имеет большую гладкость, чем предыдущая.
Пусть входная последовательность задается восьмью отсчетами 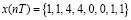 . Рассмотрим реализацию крупномасштабного преобразования сигнала с использованием вейвлетов Db4. Из определения коэффициентов следует, что данное преобразование использует четыре коэффициента фильтра. Значения коэффициентов приведены в работах [9, 10]. Эти значения будут определяться следующими значениями
. Рассмотрим реализацию крупномасштабного преобразования сигнала с использованием вейвлетов Db4. Из определения коэффициентов следует, что данное преобразование использует четыре коэффициента фильтра. Значения коэффициентов приведены в работах [9, 10]. Эти значения будут определяться следующими значениями
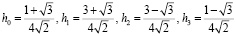 .
.
Тогда матрица преобразования Добеши будет иметь следующий вид
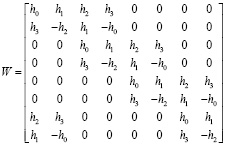 (12)
(12)
В работах [9, 10] показано, что матрица W является ортогональной, если четыре порождающие ее коэффициента удовлетворяют соотношениям
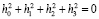 . (13)
. (13)
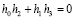 . (14)
. (14)
Кроме того для построения вейвлет-преобразования необходимо выполнение еще двух условий
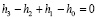 . (15)
. (15)
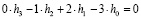 . (16)
. (16)
Эти два уравнения для вычисления коэффициентов фильтра предопределяются условием равенства нулю первых двух моментов последовательности.
При использовании этой матрицы к исходной входной последовательности получаем следующий результат
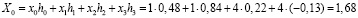 ;
;
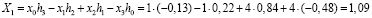 ;
;
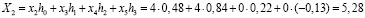 ;
;
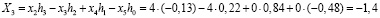 ;
;
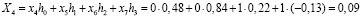 ;
;
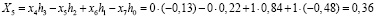 ;
;
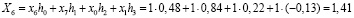 ;
;
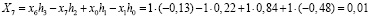 .
.
Таким образом, в ходе проведения крупномасштабного вейвлет преобразования Db4 получен образ сигнала, состоящий из 4 гладких коэффициентов, которые соответствуют четным спектральным составляющим 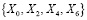 , которые вместе образуют основу сглаживающего фильтра Н.
, которые вместе образуют основу сглаживающего фильтра Н.
Очевидно, что вторая строка, представленной выше матрицы W, порождает величину 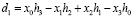 , которая является детальным коэффициентом вейвлет-преобразования. При этом все остальные четные строки порождающей матрицы будут определяться аналогичными свертками. В результате все детальные коэффициенты составят фильтры высокой частоты G. Такой фильтр G не относится к сглаживающим фильтрам. При этом его коэффициенты подобраны так, чтобы фильтр G выдавал на выход маленькие числа, когда входные данные коррелированы. Взятые вместе полученные фильтры Н и G имеют зеркальную структуру, поэтому они называются квадратурными зеркальными фильтрами (QMF, quadrature mirror filters) [10].
, которая является детальным коэффициентом вейвлет-преобразования. При этом все остальные четные строки порождающей матрицы будут определяться аналогичными свертками. В результате все детальные коэффициенты составят фильтры высокой частоты G. Такой фильтр G не относится к сглаживающим фильтрам. При этом его коэффициенты подобраны так, чтобы фильтр G выдавал на выход маленькие числа, когда входные данные коррелированы. Взятые вместе полученные фильтры Н и G имеют зеркальную структуру, поэтому они называются квадратурными зеркальными фильтрами (QMF, quadrature mirror filters) [10].
Таким образом, очевидно, что вейвлет-преобразование любого сигнла можно представить в виде прохождения исходного образа через фильтр QMF, который состоит из низкочастотного фильтра (Н) и высокочастотного фильтра (G).
Следовательно, если размер матрицы представляет собой 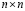 используя такую матрицу можно получить
используя такую матрицу можно получить 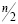 гладких коэффициентов. При этом эта матрица также порождает
гладких коэффициентов. При этом эта матрица также порождает 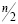 детальных коэффициентов.
детальных коэффициентов.
Рассмотрим процедуру восстановления сигнала, используя обратное вейвлет преобразование. Для осуществления данной операции необходимо использовать транспонированную матрицу (12). Тогда матрица обратного преобразования Добеши будет иметь следующий вид
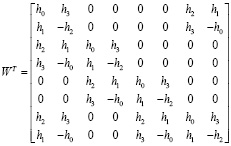 . (12)
. (12)
При использовании этой матрицы к вычисленной спектральной входной последовательности получаем следующий результат
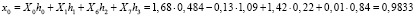 ;
;
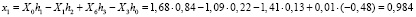 ;
;
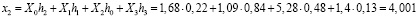 ;
;
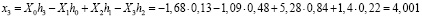 ;
;
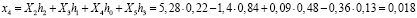 ;
;
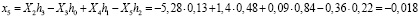 ;
;
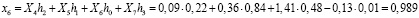 ;
;
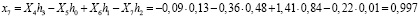 ;
;
Вычисленные данные свидетельствуют, что использование вейвлет-преобразований представляет собой обратимые преобразования. При этом из-за ошибок округления, которые определяются позиционной системой счисления, конечный результат обратного вейвлет-преобразования несколько отличается от исходного. Одним из путей решения данной проблемы может быть связано с использованием непозиционных модулярных кодов. Реализуемая ими целочисленная обработка позволит сократить ошибки округления. Применение системы остаточных классов для реализации вейвлет-преобразования Добеши показано в работах [9, 10].
Выводы
В работе рассмотрены вопросы применения модулярных кодов для реализации алгоритмов цифровой обработки сигналов. Проведенные исследования показали, что использование непозиционных модулярных кодов возможно не только при выполнении ортогональных преобразований в поле комплексных числе, но и при вейвлет-преобразованиях сигнала. В качестве такого преобразования предлагается использовать преобразования Добеши. Приведены примеры прямого преобразования Добеши, а также реализация обратного преобразования Добеши. Показана возможность использования системы остаточных классов для реализации вейвлет-преобразования. Применение малоразрядных остатков позволит повысить скорость выполнения данного преобразования сигналов.



