Существует три основных способа закраски объектов, заданных полигональными сетками. В порядке возрастания сложности ими являются: однотонная закраска, закраска, основанная на интерполяции значений интенсивности, и закраска, построенная на основе интерполяции векторов нормали [1].
Используя терминологию Сазерленда, Спрулла и Шумахера [2] (хотя они ввели классификацию алгоритмов удаления невидимых поверхностей), все эти методы можно скорее отнести к алгоритмам, работающим в пространстве изображения.Единственная информация, которая получается из пространства объекта – это нормали к граням и вектора в узлах полигональной сетки (или углы между векторами, в зависимости от выбранной модели отражения света [3]). В любой другой точке, отличной от узла полигональной сетки, восстановление например вектора нормали, будет невозможным. Это приводит к получению менее реалистичных изображений, чем хотелось бы, к появлению полос Маха, к необходимости использовать интерполяцию векторов, и т.д.
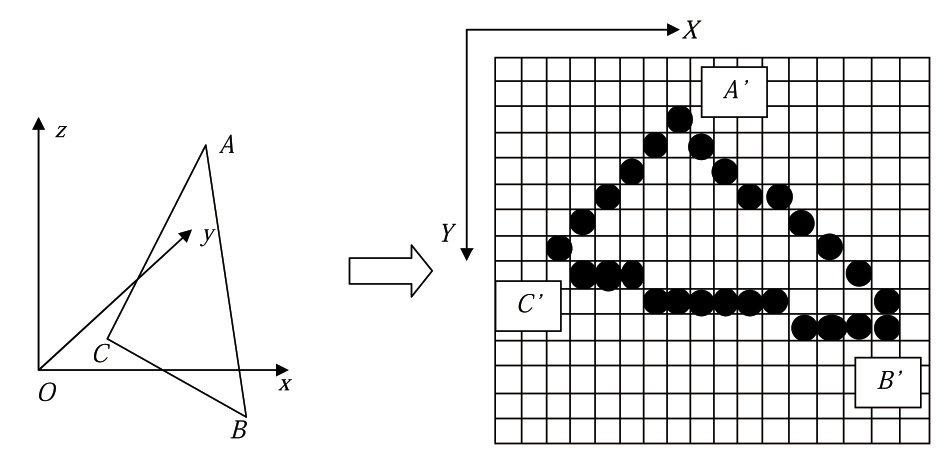
Будем считать, что объект задан набором треугольных граней.Рассмотрим один такой треугольник АВС с координатами вершин в пространстве объекта (xA, yA, zA), (xB, yB, zB) и (xC, yC, zC). После отображения (рис. 1) треугольник преобразуется в АˈВˈСˈ с координатами вершин в пространстве изображения (XA, YA), (XB, YB) и (XC, YC).
|
|
|
Рисунок 1 – Отображение треугольника |
Введем величину n, которая будет вычисляться следующим образом:
![]()
Как видно, n будет равняться наибольшему количеству приращений координаты X или Y при построении растрового изображения сторон треугольника (см. алгоритм Брезенхема [1, 3]).
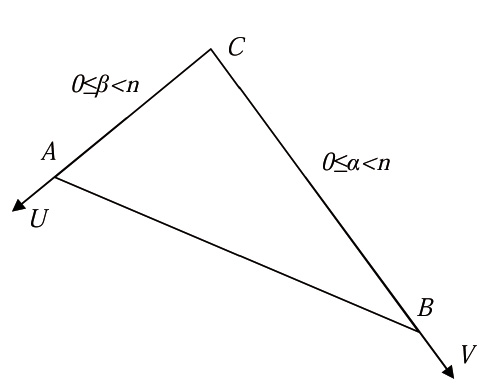
Рассмотрим параметрическое представление треугольника. Известно, что для параметрического задания отрезка необходим один параметр. Значит для представления треугольника введем два параметра α и β (рис. 2).
|
|
|
Рисунок 2 –Параметрическое задание треугольника |
При таком описании точка A имеет координаты α=0, β=n-1. Остальные вершины: B(n -1,0), C(0,0). Тогда любую точку D отрезка AC можно задать линейной комбинацией
![]()
Аналогично представляется любая точка E отрезка BC:
![]()
Теперь нетрудно представить любую точку F треугольника в виде линейной комбинации точек D и E:
![]()
Тогда алгоритм закраски треугольника будет выглядеть следующим образом:
for(α=0; α<n; α++)
{
for(β=0; α+β<n; β++)
{
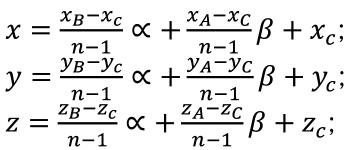
Получить цвет точки (x, y, z);
Перевести точку (x, y, z) в экранные координаты – точка (X, Y);
Поставить точку (X, Y);
}
}
Следует обратить внимание, что на отрезке AB необходимо учитывать сразу два параметра, при этом α+β<n.
То, что отрезки делятся на n частей, гарантирует отсутствие просветов в закрашенном треугольнике. Однако, правило вычисления n не исключает наложений точек, что приводит к многократной обработке одной и той же точки на экране.